В течение девяти последовательных недель фиксировался спрос Y(t) (млн. руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен в табл. 3.
Таблица 3. Исходные данные
| t | |||||||||
| Y(t) |
Задание:
1. Проверить наличие аномальных наблюдений.
2. Построить линейную модель 
, параметры которой оценить МНК;
3. Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения.
4. Осуществить прогноз спроса на следующие 2 недели (прогнозный интервал рассчитать при доверительной вероятности 70%).
5. Представить графически фактические значения показателя, результаты моделирования и прогнозирования.
Решение:
1. Проверить наличие аномальных наблюдений.
Используем метод Ирвина, основанный на определении 
– статистик по формуле
,
где 
- выборочное среднее квадратическое (стандартное) отклонение признака Y.
Подготовим 
(функция СТАНДОТКЛН) и рассчитаем - статистики.
Результаты расчетов приведем в таблице.
| Исходные данные | 1. Проверка аномальных наблюдений | |||||
| t | Y(t) | t | ||||
| 0,532152 | Sy = | 7,516648 | ||||
| 0,399114 | ||||||
| 0,133038 | ||||||
| 0,532152 | ||||||
| 0,266076 | ||||||
| 0,532152 | ||||||
| 0,532152 | ||||||
| 0,266076 | ||||||
При 
и уровне значимости 
можно использовать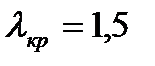 
.
Схема проверки:
не аном. аном.
0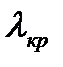 
Т.к. все, < 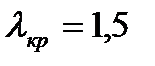следовательно, все наблюдения не аномальные.
2. Построить линейную модель временного ряда , параметры которой оценить МНК;
С помощью программы РЕГРЕССИЯ найдем коэффициенты уравнения регрессии a и b (рис. 18).
| Коэффициенты | |
| Y-пересечение | 1,166666667 |
| Переменная X 1 | 2,7 |
Таким образом,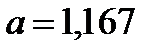 
; 
.
Модель построена, ее уравнение имеет вид 
.
Коэффициент регрессии 
показывает, что с каждой неделей спрос на кредитные ресурсы (Y) увеличивается в среднем на 2,7 млн. руб.
3. Оценить адекватность построенной модели, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения.
Проверка перечисленных свойств состоит в исследовании ряда остатков 
, который содержится в таблице «Вывод остатка» итогов РЕГРЕССИИ.
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное Y | Остатки |
| 3,866666667 | -0,866666667 | |
| 6,566666667 | 0,433333333 | |
| 9,266666667 | 0,733333333 | |
| 11,96666667 | -0,966666667 | |
| 14,66666667 | 0,333333333 | |
| 17,36666667 | -0,366666667 | |
| 20,06666667 | 0,933333333 | |
| 22,76666667 | 2,233333333 | |
| 25,46666667 | -2,466666667 |
Для проверки свойства независимости остаточной компоненты используем критерий Дарбина-Уотсона.
Согласно этому критерию вычислим по формуле статистику
.
Подготовим для вычислений: 
(функция СУММКВ), 
(функция СУММКВРАЗН).
Таким образом, 
.
По таблице d- статистик Дарбина-Уотсона определим критические уровни: нижний 
и верхний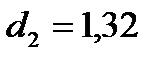 
.
Сравним полученную фактическую величину d с критическими уровнями 
и 
и сделаем вывод согласно схеме:
доп.
вып. пров. вып. вспом. d¢ = 4 - d
0 d 1 d 2 2 4 d
Полученное значение 
, что свидетельствеут об отрицательной корреляции. Перейдем к d¢ = 4 – d=1,79 и сравним с двуми критическими уровнями и 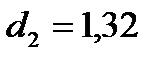. d¢ = 1,79 лежит в интервале от 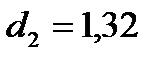до 2, следовательно, свойство независимости остаточной компоненты выполняется.
Для проверки свойства случайности остаточной компоненты используем критерий поворотных точек (пиков), основой которого является определение количества поворотных точек для ряда остатков.
С помощью Мастера диаграмм построим график остатков 
(рис. 20).
Поворотными считаются точки максимумов и минимумов на этом графике (в данном случае - третья, четвертая, пятая, шестая и восьмая). Их количество 
.
По формуле 
при 
вычислим критическое значение 
.
Сравним значения p и 
и сделаем вывод согласно схеме:
не вып. вып.
0 
, следовательно, свойство случайности для ряда остатков выполняется.
Для проверки соответствия ряда остатков нормальному закону распределения используем R/S критерий.
В соответствии с этим критерием вычислим по формуле статистику
Подготовим для вычислений:
– максимальный уровень ряда остатков (функция МАКС);
– минимальный уровень ряда остатков (функция МИН);
– стандартная ошибка модели (таблица «Регрессионная статистика» вывода итогов РЕГРЕССИИ)
Получим 
.
По таблице критических границ отношения R/S определим критический интервал. При можно использовать (2,50; 3,40).
Сопоставим фактическую величину R/S с критическим интервалом и сделаем вывод согласно схеме:
не вып. вып. не вып.
критич. интервал R/S
, значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.
Вывод: Проведенная проверка показывает, что для построенной модели выполняются все свойства. Таким образом, данная трендовая модель является адекватной реальному ряду наблюдений, её можно использовать для построения прогнозных оценок.
4. Оценить точность модели на основе использования средней относительной ошибки аппроксимации.
Используем исходные данные 
и найденные программой РЕГРЕССИЯ остатки 
(таблица «Вывод остатка»). По формуле 
рассчитаем столбец относительных погрешностей и найдем среднее значение 
.
Сравнение показывает, что 
. Следовательно, точность модели удовлетворительная.
5. Осуществить прогноз спроса на следующие 2 недели (прогнозный интервал рассчитать при доверительной вероятности 70%).
Следующие 2 недели соответствуют периодам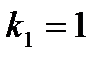 
и 
, при этом 
и 
.
Согласно уравнению модели получим точечные прогнозные оценк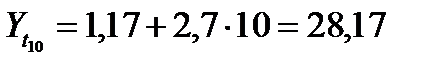и
и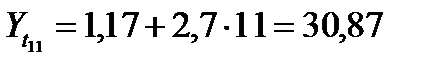 
Таким образом, ожидаемый спрос на кредитные ресурсы финансовой компании в следующие 2 недели будет составлять около 28,17 млн. руб. и 30,87 млн. руб. соответственно.
Для оценки точности прогнозирования рассчитаем границы прогнозного интервала для индивидуальных значений результирующего признака (доверительная вероятность 
).
Подготовим:
(функция СТЬЮДРАСПОБР при 
, 
);
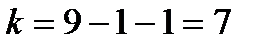(строка «стандартная ошибка» итогов РЕГРЕССИИ);
(функция СРЗНАЧ); 
(функция КВАДРОТКЛ).
Вычислим размах прогнозного интервала для индивидуальных значений, используя формулу
,
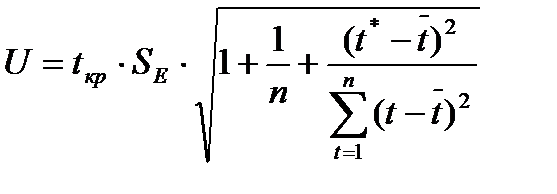При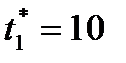 
получим 
и определим границы доверительного интервала:
; 
.
При 
получим 
и определим границы доверительного интервала:
; 
.
Таким образом, с надежностью 70% можно утверждать, что спрос на кредитные ресурсы финансовой компании на следующей (10-ой) недели будет составлять от 26,17 до 30,16 млн. руб., а через неделю (на 11-ой недели) – от 28,75 до 32,981 млн. руб.
6. Представить графически фактические значения показателя, результаты моделирования и прогнозирования.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные.
Затем с помощью опции Добавить линию тренда… построим линию модели: тип ® линейна; параметры ® показывать уравнение на диаграмме.
Покажем на графике результаты прогнозирования (рис. 21). Для этого в опции Исходные данные добавим ряды:
Имя ® прогноз; значения Х ® 
и 
; значения Y ® 
и 
;
Имя ® нижние границы; значения Х ® и ; значения Y ® 
и 
;
Имя ® верхние границы; значения Х ® и ; значения Y ® 
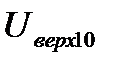и 
;
