Постановка задачи.
Имеются данные (табл. 1) о продаже квартир на вторичном рынке жилья в Московской области.
Таблица 1. Исходные данные
| № п.п. | Y | Х1 | Х2 | Х4 |
| 51,4 | ||||
| 184,6 | ||||
| 17,9 | ||||
| 60,65 | 37,8 | |||
| 70,96 | 36,9 | |||
| 39,5 | ||||
| 78,9 | 16,9 | |||
| 123,5 | 67,5 | |||
| 55,2 | 15,3 | |||
| 95,5 | ||||
| 57,6 | 31,5 | |||
| 64,5 | 34,8 | |||
| 52,3 | ||||
| 27,8 | ||||
| 17,3 | ||||
| 44,5 | ||||
| 42,1 | 19,1 | |||
| 39,6 | ||||
| 17,4 | ||||
| 34,8 | ||||
| 69,6 | ||||
| 64,5 | 30,5 | |||
| 152,3 |
Таблица 2. Наименования показателей
| Обозначение | Наименование показателя | Единица измерения |
| Y | Цена квартиры | тыс. долл. |
| X1 | Город области | 1 – Подольск |
| 0 – Люберцы | ||
| X2 | Число комнат в квартире | |
| X4 | Жилая площадь квартир | кв. м. |
Задание:
1. Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов корреляции.
2. Построить поле корреляции результативного признака и наиболее тесно связанного с ним фактора.
3. Рассчитать параметры линейных парных регрессий для всех факторов X.
4. Оценить качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F – критерия Фишера. Выбрать лучшую модель.
5. С использованием лучшей модели осуществить прогнозирование среднего значения показателя Y при уровне значимости  , если прогнозное значение фактора X составит 80% от его максимального значения. Представить графически фактические и модельные значения Y, результаты прогнозирования.
, если прогнозное значение фактора X составит 80% от его максимального значения. Представить графически фактические и модельные значения Y, результаты прогнозирования.
6. Используя пошаговую множественную регрессию (метод исключения или метод включения), построить модель формирования цены квартиры за счет значимых факторов. Дать экономическую интерпретацию коэффициентов модели регрессии.
7. Оценить качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дать оценку влияния значимых факторов на результат с помощью коэффициентов эластичности,  - и
- и  - коэффициентов.
- коэффициентов.
Решение.
1. Рассчитать матрицу парных коэффициентов корреляции; оценить статистическую значимость коэффициентов корреляции.
Для построения матрицы парных коэффициентов корреляции с помощью Excel выполним следующие действия Сервис ® Анализ данных ® КОРРЕЛЯЦИЯ.
Получим матрицу коэффициентов парной корреляции между всеми имеющимися переменными:

Проанализируем коэффициенты корреляции между результирующим признаком Y и каждым из фактором 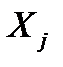 :
:
 , следовательно, между переменными Y и
, следовательно, между переменными Y и  наблюдается обратная корреляционная зависимость: цена квартиры ниже для квартир из Подольска.
наблюдается обратная корреляционная зависимость: цена квартиры ниже для квартир из Подольска.
 – эта зависимость является умеренной ближе к слабой.
– эта зависимость является умеренной ближе к слабой.
 , значит, между переменными Y и
, значит, между переменными Y и  наблюдается прямая корреляционная зависимость: чем больше комнат в квартире, тем выше цена квартиры.
наблюдается прямая корреляционная зависимость: чем больше комнат в квартире, тем выше цена квартиры.
 – эта зависимость умеренная ближе к тесной.
– эта зависимость умеренная ближе к тесной.
 , значит, между переменными Y и
, значит, между переменными Y и  наблюдается прямая корреляционная зависимость: чем больше площадь квартиры, тем выше цена квартиры.
наблюдается прямая корреляционная зависимость: чем больше площадь квартиры, тем выше цена квартиры.
 – эта зависимость тесная.
– эта зависимость тесная.
Для проверки значимости найденных коэффициентов корреляции используем критерий Стьюдента.
Для каждого коэффициента корреляции  вычислим t -статистику по формуле
вычислим t -статистику по формуле  (рис. 4). Критическое значение t-статистики Стьюдента при уровне значимости 0,05 и числе степеней свободы 38: tрасч≈ 2,02439415
(рис. 4). Критическое значение t-статистики Стьюдента при уровне значимости 0,05 и числе степеней свободы 38: tрасч≈ 2,02439415

Рис.4.
 , следовательно, коэффициент
, следовательно, коэффициент 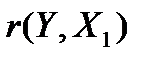 значимо отличается от нуля. На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии линейной корреляционной связи между признаками Y и
значимо отличается от нуля. На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии линейной корреляционной связи между признаками Y и  , зависимость цены квартиры Y от города области
, зависимость цены квартиры Y от города области  является достоверной.
является достоверной.
 , следовательно, коэффициент
, следовательно, коэффициент  значимо отличается от нуля. На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии линейной корреляционной связи между признаками Y и
значимо отличается от нуля. На уровне значимости 5% выборочные данные позволяют сделать вывод о наличии линейной корреляционной связи между признаками Y и  , зависимость цены квартиры Y от числа комнат в квартире
, зависимость цены квартиры Y от числа комнат в квартире  является достоверной.
является достоверной.
 , следовательно, коэффициент
, следовательно, коэффициент  значимо отличается от нуля. На основе выборочных данных можно сделать вывод о наличии линейной корреляционной связи между признаками Y и
значимо отличается от нуля. На основе выборочных данных можно сделать вывод о наличии линейной корреляционной связи между признаками Y и 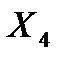 , зависимость цены квартиры Y от общей площади квартиры
, зависимость цены квартиры Y от общей площади квартиры  является достоверной.
является достоверной.
Анализ матрицы коэффициентов парной корреляции показывает, что наиболее тесная и значимая зависимость наблюдается между ценой квартиры Y и общей площадью квартиры  .
.
2. Построить поле корреляции результативного признака и наиболее тесно связанного с ним фактора.
Для построения поля корреляции используем Мастер диаграмм (точечная) – покажем исходные данные Y и значения наиболее информативного фактора 

3.Рассчитать параметры линейных парных регрессий для всех факторов X.
Для построения парной модели  используем программу РЕГРЕССИЯ (Сервис ® Анализ данных). В качестве «входного интервала X» покажем значения фактора
используем программу РЕГРЕССИЯ (Сервис ® Анализ данных). В качестве «входного интервала X» покажем значения фактора  .Результаты вычислений представлены в таблицах:
.Результаты вычислений представлены в таблицах:

Коэффициенты модели содержатся в третьей таблице итогов РЕГРЕССИИ (столбец Коэффициенты).
Таким образом, модель (1) построена, ее уравнение имеет вид
 .
.
Коэффициент регрессии 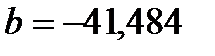 , следовательно, цена квартиры в Подольске в среднем на 41,484 тыс. долл. ниже цены квартиры в Люберцы.
, следовательно, цена квартиры в Подольске в среднем на 41,484 тыс. долл. ниже цены квартиры в Люберцы.
Свободный член  в данном уравнении не имеет реального смысла.
в данном уравнении не имеет реального смысла.
Аналогичные расчеты проведем для построения модели зависимости цены квартиры Y от числа комнат в квартире  (рис. 2).
(рис. 2).

Таким образом, модель (2) построена, ее уравнение имеет вид
. 
Коэффициент регрессии  , следовательно, при увеличении числа комнат в квартире
, следовательно, при увеличении числа комнат в квартире  на 1 комнату цена квартиры (Y) увеличивается в среднем на 33,516 тыс. долл.
на 1 комнату цена квартиры (Y) увеличивается в среднем на 33,516 тыс. долл.
Свободный член  в данном уравнении не имеет реального смысла.
в данном уравнении не имеет реального смысла.
Так же построим модель зависимости цены квартиры Y от жилой площади квартиры  (рис. 3).
(рис. 3).
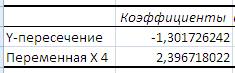
Модель (3) построена, ее уравнение имеет вид

Коэффициент регрессии  , следовательно, при увеличении жилой площади квартиры
, следовательно, при увеличении жилой площади квартиры  на 1 кв. м. цена квартиры (Y) увеличивается в среднем на 2,397 тыс. долл.
на 1 кв. м. цена квартиры (Y) увеличивается в среднем на 2,397 тыс. долл.
Свободный член  не имеет реального смысла.
не имеет реального смысла.
4.Оценить качество каждой модели через коэффициент детерминации, среднюю ошибку аппроксимации и F – критерия Фишера. Выбрать лучшую модель.
Коэффициенты детерминации R-квадрат определены для каждой модели программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляют:
| Модель | R-квадрат |
 (1) (1)
| 0,16268 |
 (2) (2)
| 0,47363 |
 (3) (3)
| 0,68292 |
Таким образом, вариация (изменение) цены квартиры Y на 16,27% объясняется по уравнению (1) изменением расположения квартиры в городах области  ; на 47,36% объясняется по уравнению (2) вариацией числа комнат в квартире
; на 47,36% объясняется по уравнению (2) вариацией числа комнат в квартире  ; на 68,30% по уравнению (3) изменением жилой площади квартиры
; на 68,30% по уравнению (3) изменением жилой площади квартиры  .
.
Для вычисления средней относительной ошибки аппроксимации рассмотрим остатки модели  , содержащиеся в столбце «Остатки» итогов программы РЕГРЕССИЯ (таблица «Вывод остатка»). Дополним таблицу столбцом относительных погрешностей, которые вычислим по формуле
, содержащиеся в столбце «Остатки» итогов программы РЕГРЕССИЯ (таблица «Вывод остатка»). Дополним таблицу столбцом относительных погрешностей, которые вычислим по формуле  с помощью функции ABS.
с помощью функции ABS.
Покажем выполнение расчетов для модели (1).

По столбцу относительных погрешностей найдем среднее значение  (функция СРЗНАЧ).
(функция СРЗНАЧ).
Выполнив аналогичные расчеты для моделей (2) и (3), результаты занесем в сводную таблицу:
| Модель | R-квадрат | 
| |||
 (1) (1)
| 0,16268 | 36,90% | |||
 (2) (2)
| 0,47363 | 27,86% | |||
 (3) (3)
| 0,68292 | 26,17% | |||
Оценим точность построенных моделей в соответствии со схемой:
0% 5% 15% 
 ,
, 
 – модель (1), (2) и (3) имеет неудовлетворительную точность.
– модель (1), (2) и (3) имеет неудовлетворительную точность.
Проверим значимость полученных уравнений с помощью F-критерия Фишера. F – статистики определены программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляют:
| Модель | R-квадрат | 
| F |
 (1) (1)
| 0,16268 | 36,90% | 7,3828 |
 (2) (2)
| 0,47363 | 27,86% | 34,1930 |
 (3) (3)
| 0,71496 | 26,1662% | 81,8439 |
Критическое значение  найдено для уравнения значимости
найдено для уравнения значимости  и чисел степеней свободы
и чисел степеней свободы  ,
,  (функция FРАСПОБР).
(функция FРАСПОБР).
Схема проверки:
не знач. знач.
0 
Сравнение показывает:  ,
,  и
и  ; следовательно, уравнения моделей (1), (2) и (3) являются значимыми, их использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенными в модели факторными переменными
; следовательно, уравнения моделей (1), (2) и (3) являются значимыми, их использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенными в модели факторными переменными  ,
,  и
и  .
.
Вывод: на основании оценки качества моделей по коэффициенту детерминации, средней ошибке аппроксимации и критерию Фишера наилучшей является модель (3) зависимости цены квартиры от жилой площади квартиры.
5.С использованием лучшей модели осуществить прогнозирование среднего значения показателя Y при уровне значимости  , если прогнозное значение фактора X составит 80% от его максимального значения. Представить графически фактические и модельные значения Y, результаты прогнозирования.
, если прогнозное значение фактора X составит 80% от его максимального значения. Представить графически фактические и модельные значения Y, результаты прогнозирования.
Согласно условию задачи прогнозное значение факторной переменной  составит
составит  (функция МАКС). Рассчитаем по уравнению модели (3) прогнозное значение показателя Y:
(функция МАКС). Рассчитаем по уравнению модели (3) прогнозное значение показателя Y:

Таким образом, если жилая площадь квартиры составит 80% от его максимального значения и будет равна 67,2 кв.м., то ожидаемая цена квартиры будет около 159,758тыс. долл.
Зададим доверительную вероятность  и построим доверительный прогнозный интервал для среднего значения Y.
и построим доверительный прогнозный интервал для среднего значения Y.
Для этого нужно рассчитать стандартную ошибку прогнозирования для среднего значения результирующего признака
 .
.
Предварительно подготовим:
· Стандартную ошибку модели  (таблица «Регрессионная статистика» итогов РЕГРЕССИИ);
(таблица «Регрессионная статистика» итогов РЕГРЕССИИ);
· По столбцу исходных данных  найдем среднее значение
найдем среднее значение  (функция СРЗНАЧ) и определим
(функция СРЗНАЧ) и определим  (функция КВАДРОТКЛ);
(функция КВАДРОТКЛ);
· 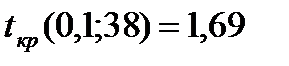 (функция СТЬЮДРАСПОБР).
(функция СТЬЮДРАСПОБР).
Следовательно, стандартная ошибка прогнозирования для среднего значения составляет
 .
.
Размах доверительного интервала для среднего значения:
 .
.
Границами прогнозного интервала будут
 ;
;
 .
.
Таким образом, с надежностью 90% можно утверждать, что если жилая площадь квартиры составит 80% от его максимального значения и будет равна 67,2 кв.м., то ожидаемая средняя цена квартиры будет от 145,16 до 174,355 тыс. долл.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).
Затем с помощью опции Добавить линию тренда… построим линию модели: тип ® линейная; параметры ® показывать уравнение на диаграмме.
Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:
Имя ® прогноз; значения Х ®  ; значения Y ®
; значения Y ®  ;
;
Имя ® нижняя граница; значения Х ®  ; значения Y ®
; значения Y ®  ;
;
Имя ® верхняя граница; значения Х ®  ; значения Y ®
; значения Y ®  .
.

6.Используя пошаговую множественную регрессию (метод исключения), построить модель формирования цены квартиры за счет значимых факторов. Дать экономическую интерпретацию коэффициентов модели регрессии.
Множественные модели:

|

|

|
Построим множественную модель с помощью программы Регрессия, учитывая все факторы (  ,
,  и
и  ), получим:
), получим:
Построим множественную модель с помощью программы Регрессия, учитывая все факторы (  ,
,  и
и  ), получим:
), получим:
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 30,45004571 | 10,14617717 | 3,001134832 | 0,004862638 |
| Х1 | -36,17638013 | 7,070149312 | -5,116777389 | 1,05101E-05 |
| Х2 | -28,53160128 | 8,441863622 | -3,379775197 | 0,00175709 |
| Х4 | 3,848740227 | 0,499544248 | 7,704503136 | 3,99877E-09 |
Получаем модель вида:
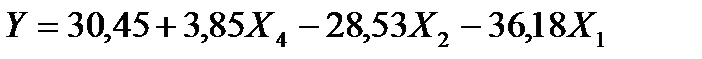 .
.
Проверим значимость полученного уравнения с помощью F-критерия Фишера. F-статистика определена программой РЕГРЕССИЯ.
Поскольку  уравнение регрессии следует признать адекватным.
уравнение регрессии следует признать адекватным.
С помощью t -критерия Стьюдента проверим значимость отдельных коэффициентов модели.
Критическое значение 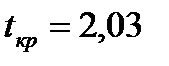 найдено для уровня значимости
найдено для уровня значимости  и числа степеней свободы
и числа степеней свободы  (функция СТЬЮДРАСПОБР).
(функция СТЬЮДРАСПОБР).
Схема проверки:
не знач. знач.
0  ½ t ½
½ t ½
Выберем наименьшее по модулю значение t-критерия Стьюдента. Это коэффициент 
Рассмотрим коэффициенты парной корелляции независимых переменных X2 (число комнат в квартире) и X4 (жилая площадь квартиры)  = 0,92. Так как это больше 0,8, следовательно в исходных данных имеется мультиколлинеарность. Чтобы избавиться от мультиколлинеарности из переменных
= 0,92. Так как это больше 0,8, следовательно в исходных данных имеется мультиколлинеарность. Чтобы избавиться от мультиколлинеарности из переменных  (число комнат в квартире) и
(число комнат в квартире) и  (жилая площадь квартиры) оставим в модели
(жилая площадь квартиры) оставим в модели  , так как он в большей степени связан с зависимой переменной Y(цена квартиры).
, так как он в большей степени связан с зависимой переменной Y(цена квартиры).
Рассмотрим следующую модель:
В качестве «входного интервала Х» укажем значения факторов  и
и  , с помощью программы регрессия найдем коэффициенты данной модели:
, с помощью программы регрессия найдем коэффициенты данной модели:
| Коэффициенты | |
| Y-пересечение | 21,44848618 |
| Х1 | -32,73940067 |
| Х4 | 2,297644203 |
Таким образом, модель зависимости цены квартиры Y от города области  и жилой площади квартиры
и жилой площади квартиры 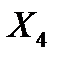 построена, ее уравнение имеет вид
построена, ее уравнение имеет вид
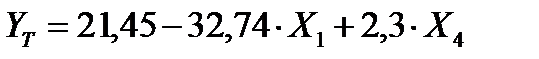 .
.
Оценим качество модели.
Поскольку  , уравнение регрессии следует признать адекватным.
, уравнение регрессии следует признать адекватным.
С помощью t -критерия Стьюдента проверим значимость отдельных коэффициентов модели.
Критическое значение 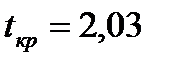 найдено для уровня значимости
найдено для уровня значимости  и числа степеней свободы
и числа степеней свободы  (функция СТЬЮДРАСПОБР).
(функция СТЬЮДРАСПОБР).
Схема проверки:
не знач. знач.
0  ½ t ½
½ t ½
Выберем наименьшее по модулю значение t-критерия Стьюдента. Это коэффициент  ., значит коэффициент регрессии является значимым.
., значит коэффициент регрессии является значимым.
Коэффициенты корелляции показывают, что мультиколлинеарность между факторами  и
и  отсутствует.
отсутствует.
Таким образом, лучшей является модель 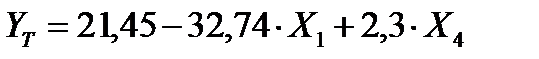 зависимость цены квартиры Y от города области
зависимость цены квартиры Y от города области  и жилой площади квартиры
и жилой площади квартиры  .
.
Коэффициент регрессии  , следовательно, при смене квартиры из города Люберцы в Подольск и неизменной жилой площади квартиры цена квартиры (Y) снижается в среднем на 32,74 тыс. долл.
, следовательно, при смене квартиры из города Люберцы в Подольск и неизменной жилой площади квартиры цена квартиры (Y) снижается в среднем на 32,74 тыс. долл.
Коэффициент регрессии  , следовательно, при увеличении жилой площади квартиры
, следовательно, при увеличении жилой площади квартиры  на 1 кв. м. и неизменном городе области цена квартиры (Y) увеличивается в среднем на 2,3 тыс. долл.
на 1 кв. м. и неизменном городе области цена квартиры (Y) увеличивается в среднем на 2,3 тыс. долл.
Свободный коэффициент не имеет экономического смысла.
7. Оценить качество построенной модели. Улучшилось ли качество модели по сравнению с однофакторной моделью? Дать оценку влияния значимых факторов на результат с помощью коэффициентов эластичности, b- и D-коэффициентов.
Для оценки качества выбранной множественной модели (4) алогично п.4 данной задачи используем коэффициент детерминации R - квадрат, среднюю относительную ошибку аппроксимации и F -критерий Фишера.
Коэффициент детерминации R - квадрат выпишем из итогов РЕГРЕССИИ (таблица «Регрессионная статистика» для модели(4)).
 , следовательно, вариация (изменение) цены квартиры Y на 78,3 % объясняется по данному уравнению вариацией города области
, следовательно, вариация (изменение) цены квартиры Y на 78,3 % объясняется по данному уравнению вариацией города области  и жилой площадь квартиры
и жилой площадь квартиры  .
.
Используем исходные данные Yi и найденные программой РЕГРЕССИЯ остатки Еi (таблица «Вывод остатка» для модели (4)). Рассчитаем относительные погрешности и найдем среднее значение  . Следовательно, точность модели неудовлетворительная.
. Следовательно, точность модели неудовлетворительная.
С помощью F -критерия Фишера проверим значимость модели в целом.
Для этого выпишем из итогов РЕГРЕССИИ (таблица «Дисперсионный анализ» для модели (4)) F = 66,78. Определим критическое значение  (функция FРАСПОБР). Сравним найденные величины
(функция FРАСПОБР). Сравним найденные величины  . Следовательно, уравнение модели (4) является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенными в модель факторными переменными
. Следовательно, уравнение модели (4) является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенными в модель факторными переменными  и
и  .
.
Дополнительно с помощью t -критерия Стьюдента проверим значимость отдельных коэффициентов модели.
t -статистики для коэффициентов уравнения регрессии приведены в итогах программы РЕГРЕССИЯ.
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | 21,44848618 | 11,0838945 | 1,935103784 | 0,060649342 |
| Х1 | -32,73940067 | 7,921039863 | -4,133220036 | 0,000196621 |
| Х4 | 2,297644203 | 0,223356507 | 10,28689171 | 2,11022E-12 |
Критическое значение  найдено для уровня значимости
найдено для уровня значимости  и числа степеней свободы
и числа степеней свободы  (функция СТЬЮДРАСПОБР).
(функция СТЬЮДРАСПОБР).
Схема проверки:
не знач. знач.
0  ½ t ½
½ t ½
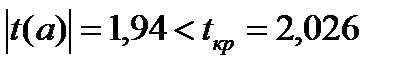 , следовательно, свободный коэффициент a не является значимым, его можно исключить из модели.
, следовательно, свободный коэффициент a не является значимым, его можно исключить из модели.
 , следовательно, коэффициент регрессии b 1 является значимым, его и фактор город области нужно сохранить в модели.
, следовательно, коэффициент регрессии b 1 является значимым, его и фактор город области нужно сохранить в модели.
 , следовательно, коэффициент регрессии b 2 является значимым, его и фактор жилая площадь квартиры нужно сохранить в модели.
, следовательно, коэффициент регрессии b 2 является значимым, его и фактор жилая площадь квартиры нужно сохранить в модели.
Выводы о значимости коэффициентов модели сделаны на уровне значимости  . Рассматривая столбец «P-значение», отметим, что свободный коэффициент a можно считать значимым на уровне 0,06 = 6%; коэффициент регрессии b 1 – на уровне 0,0002=0,02%; а коэффициент регрессии b 2 – на уровне 2,11 Е -12 ®0%.
. Рассматривая столбец «P-значение», отметим, что свободный коэффициент a можно считать значимым на уровне 0,06 = 6%; коэффициент регрессии b 1 – на уровне 0,0002=0,02%; а коэффициент регрессии b 2 – на уровне 2,11 Е -12 ®0%.
Для сравнения качества парной модели (3) и выбранной множественной модели (4) используем нормированные коэффициенты детерминации.
| Модель | Нормированный R-квадрат |
 (3) (3)
| 0,674576646 |
 (4) (4)
| 0,771351971 |
Таким образом, при добавлении в уравнение регрессии фактора «город области»  качество модели улучшилось, что говорит в пользу сохранения фактора
качество модели улучшилось, что говорит в пользу сохранения фактора  в модели.
в модели.
Средние коэффициенты эластичности в случае линейной модели определяются формулами  , где j = 1, 2, …, где
, где j = 1, 2, …, где  ,
,  – выборочные средние признаков
– выборочные средние признаков  и Y;
и Y;  - коэффициенты регрессии.
- коэффициенты регрессии.
Вычислим  ;
;  ;
;  (функция СРЗНАЧ) и найдем,
(функция СРЗНАЧ) и найдем,  ,
,  .
.
Следовательно, при увеличении фактора  на 1% и неизменном уровне жилой площади квартиры цена квартиры Y снижается в среднем на 0,201%.
на 1% и неизменном уровне жилой площади квартиры цена квартиры Y снижается в среднем на 0,201%.
Увеличение жилой площади квартиры  на 1% приводит к увеличению цены квартиры Y в среднем на 0,97% (при неизменном городе области).
на 1% приводит к увеличению цены квартиры Y в среднем на 0,97% (при неизменном городе области).
Бета- коэффициенты определяются формулами  , j = 1, 2,…, где
, j = 1, 2,…, где 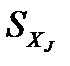 ,
,  – выборочные средние квадратичные (стандартные) отклонения признаков
– выборочные средние квадратичные (стандартные) отклонения признаков 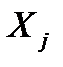 и
и  ;
;  - коэффициенты регрессии.
- коэффициенты регрессии.
Подготовим  ;
;  ;
; 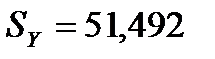 (функция СТАНДОТКЛОН) и рассчитаем
(функция СТАНДОТКЛОН) и рассчитаем  ,
, 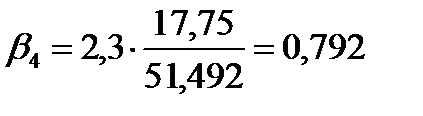 .
.
Таким образом, при увеличении только фактора  на одно его стандартное отклонение результат Y уменьшается в среднем на 0,3183 своего стандартного отклонения
на одно его стандартное отклонение результат Y уменьшается в среднем на 0,3183 своего стандартного отклонения  , а при увеличении только фактора
, а при увеличении только фактора  на одно его стандартное отклонение результат Y увеличивается в среднем на 0,792 своего стандартного отклонения
на одно его стандартное отклонение результат Y увеличивается в среднем на 0,792 своего стандартного отклонения  .
.
Дельта- коэффициенты определяются формулами  , j = 1, 2,…, где
, j = 1, 2,…, где  – соответствующие выборочные коэффициенты парной корреляции.
– соответствующие выборочные коэффициенты парной корреляции.
Коэффициенты парной корреляции 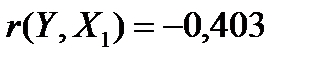 и
и  найдены с помощью программы КОРРЕЛЯЦИИ (п.1 данной задачи), коэффициент детерминации
найдены с помощью программы КОРРЕЛЯЦИИ (п.1 данной задачи), коэффициент детерминации  определен для рассматриваемой двухфакторной модели программой РЕГРЕССИЯ.
определен для рассматриваемой двухфакторной модели программой РЕГРЕССИЯ.
Вычислим дельта - коэффициенты:  ,
,  .
.
Значит, по уравнению полученной линейной двухфакторной модели изменение результирующего фактора Y (цены квартиры) на 16,4% объясняется воздействием фактора  (город области) и на 83,6% влиянием фактора
(город области) и на 83,6% влиянием фактора 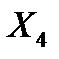 (жилая площадь квартиры).
(жилая площадь квартиры).






