Задание 1
1. Получим зависимость высоты, на которой отражается волна, от угла падения последней на ионосферу. Для этого используем следствие закона Снеллиуса:
n(z0)=n(0)sinΘ0, (1)
___
где n(z)=√ε(z), n(0) – показатель преломления в начале линейного слоя
(в воздухе) при входе в ионосферу, а значит n(0)=1.
Соотношение (1) соответствует условию полного внутреннего отражения
sinΘ n(z0)=n(0)sinΘ0 ,
имеющему место при Θ=π/2 в точке z= z0 (в точке разворота).
Выведем формулу для нахождения точки разворота:
,
,
ε(z)=1-80,8 N(z)/f2,
N0=0 (в нашем случае),
тогда используя две вышеприведённые формулы получим:
, (2)
используя формулу (1) получим
используя дальнейшие математические преобразования получаем
(3)
Отсюда получаем, что
2. Получим зависимость расстояния, проходимого волной, от угла падения на ионосферу.
(4)
здесь х1=zн tап(Θ0), нижняя граница интеграла-это нижняя граница ионосферы, верхняя-точка разворота.
Вычислим данный интеграл и выведем уравнение (4):
подставляя вместо 
выражение (2), получим
Тогда
Подставим вместо 
выражение (3)
учитывая, что х1=zн tап(Θ0), то
Тогда для всей траектории движения уравнение будет иметь вид:
3. Вычисление фазы поля в точке падения отражённой волны на поверхность Земли.
Изменение фазы волны в результате отражения при наклонном падении равно:
где (x2-x1)=2 zн tап(Θ0), 
Вычислим данный интеграл:
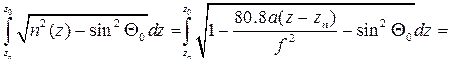
Тогда с учётом (x2-x1)=2 zн tап(Θ0), 
получим
Зная зависимость координаты и фазы от угла Θ, можно построить зависимость модуля напряжённости поля Е от координаты Х вблизи точки падения.
Программа.
График зависимости модуля поля на уровне 2*106
и в диапазоне от -2 до +2
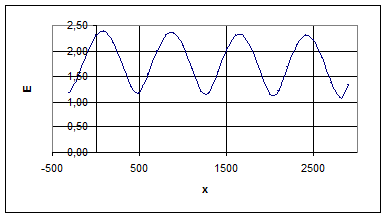
Задание 1
Расчёт поля в точке отражения волны от ионосферы.
Для данного вычисления воспользуемся формулами:
,
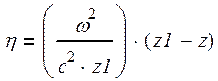
при η>0,
,
при η<0.
Где
-постоянная,
- функции Бесселя порядка 1/3 и -1/3,
z1-точка преломления, с-скорость света,
ω=2πf – циклическая частота.
Расчёт поля в точке отражения волны производим с помощью программы.
Программа для расчёта поля Е(z).
clc
a=10^7;
z0=220;
theta1=pi/4;
N0=10^8;
f=1.5*(10^6);
z1=(((f*cos(theta1))^2)/(80.8*a))-N0/a+z0;
z1
c=300000;
w=2*pi*f;
A=(2/3)*(sqrt(pi))*((w*z1/c)^(1/6));
hold on
z=z1-500:20:z1;
et=(((w^2)/((c^2)*z1))^(1/3))*(z1-z);
E=A*(et.^(1/2)).*(besselj(1/3,((2/3)*(et.^(3/2)))))+A*(et.^(1/2)).*(besselj(-1/3,((2/3)*(et.^(3/2)))));
r=0;
plot(z,E);
plot(z,r);
z=z1:20:z1+500;
et=(((w^2)/((c^2)*z1))^(1/3))*(z1-z);
K=A*((-et).^(1/2)).*(-besseli(1/3,((2/3)*((-et).^(3/2)))))+A*((-et).^(1/2)).*(besseli(-1/3,((2/3)*((-et).^(3/2)))));
r=0;
plot(z,r);
plot(z,K);
y=-15:0.1:15;
plot(z1,y);
grid on
xlabel('z')
ylabel('E')
hold off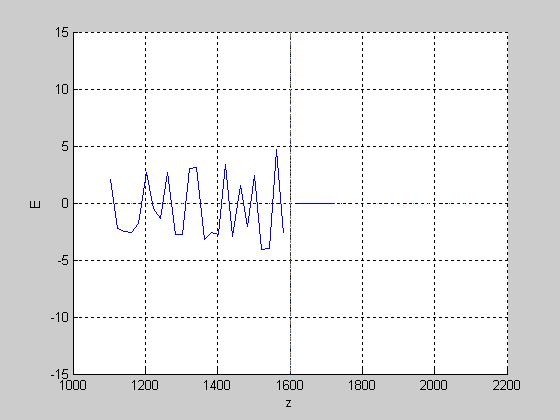 
График зависимости поля Е от координаты Z вблизи точки отражения.
Программа для расчёта поля Е(η).
a=10^7;
z0=220;
theta1=pi/4;
f=1500000;
N0=10^8;
z1=(((f*cos(theta1))^2)/(80.8*a))-N0/a+z0;
c=300000;
w=2*pi*f
A=(2/3)*(sqrt(pi))*((w*z1/c)^(1/6))
hold on
z=z1-500:20:z1
et=(((w^2)/((c^2)*z1))^(1/3))*(z1-z)
E=A*(et.^(1/2)).*(besselj(1/3,((2/3)*(et.^(3/2)))))+A*(et.^(1/2)).*(besselj(-1/3,((2/3)*(et.^(3/2)))))
plot(et,E)
z=z1:20:z1+200
et=(((w^2)/((c^2)*z1))^(1/3))*(z1-z)
K=A*((-et).^(1/2)).*(-besseli(1/3,((2/3)*((-et).^(3/2)))))+A*((-et).^(1/2)).*(besseli(-1/3,((2/3)*((-et).^(3/2)))))
plot(et,K)
y=-15:0.1:15
grid on
xlabel('et')
ylabel('E')
hold off
График зависимости поля Е от η вблизи точки отражения.
Где z1= 1.6023e+003–точка отражения.
Вывод: В результате проделанной работы мы нашли поле вдоль поверхности Земли в заданной точке и диапазоне, а также в точке отражения волны от ионосферы. В точке падения волны на Землю сигнал слабый, однако в заданном диапазоне имеются несколько максимумов. В точке отражения от ионосферы, амплитуда волны близка к максимуму, выше неё, амплитуда убывает, а ниже этой точки амплитуда достигает своего максимума, но затем плавно убывает по модулю.
Литература:
1. А. Н. Братчиков, В. С. Темченко, В. С. Филлипов Расчёт
электромагнитных полей в слоистых и периодических
структурах. – М.; издательство МАИ, 1989.
2. В. Г. Потёмкин «Система инженерных и научных расчётов
Мatlab»
