Рассмотрим Т d - задачу:
Минимизировать
при условиях
Введем следующие определения.
1. Элемент сij = 0 матрицы С называется Х - неполным нулем, если в плане Х Тd - задачи элемент хij < dij. Если же хij = dij, то элемент сij называется Х - полным нулем.
2. Х - существенным нулем матрицы С называется такой ее элемент сij = 0, для которого хij > 0, в противном случае этот элемент называется несущественным нулем.
Описание алгоритма венгерского метода. Алгоритм решения Т d -задачи, основанный на венгерском методе, состоит из предварительного этапа и ряда однотипных итераций [18; 59].
Предварительный этап. Его цель - приведение матрицы С и построение начального приближения к решению Х 0.
В каждом столбце матрицы С разыскивают минимальный элемент и вычитают из всех элементов данного столбца. В результате получают матрицу С '. Далее, из всех элементов каждой строки С ' вычитают минимальный элемент этой строки и получают в результате матрицу С 0(С 0@ С), в каждой строке и столбце которой имеется хотя бы один нуль.
После этого формируют матрицу Х 0=|| xij 0 ||, процесс построения которой ведут по столбцам. Пусть уже заполнены первые (j -1) столбцы матрицы Х 0. Перенумеруем нули j-го столбца матрицы С0 сверху вниз и через ikj (k =1,2,., r) обозначим номер строки, содержащей k-й нуль j -го столбца. Тогда элементы j -го столбца определяются в соответствии с формулой
если 
k=1,2.. (3.3.21)
Если для матрицы Х 0 суммарная невязка
то Х 0 - оптимальной план Т d -задачи.
Если же D0>0, то переходят к первой итерации.
Каждая итерация алгоритма в общем случае включает 3 этапа: начинается первым этапом, затем несколько раз могут повторяться первый и третий этапы, а заканчивается итерация вторым этапом либо установлением неразрешимости данной задачи.
(k +1)-я итерация. Предположим, что уже осуществлено k итераций алгоритма, в результате которых получены матрицы Х k и С k.
Пусть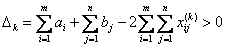 
и еще не установлена неразрешимость Тa-задачи.
Целью (k +1)-й итерации является построение матрицы Х k +1 и проверка ее на оптимальность или на установление неразрешимости Т d -задачи. Перед началом итерации знаком '+' выделяют те столбцы матрицы С k, для которых невязка
.
Первый этап. Выбирают произвольный невыделенный Х k - неполный нуль матрицы С k, если это элемент С ijk, то вычисляют невязку строки i, его содержащей:
.
Тогда возможен один из двух случаев:
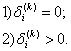
Во втором случае, отметив этот невыделенный нуль cijk =0 знаком штрих, сразу переходим ко второму этапу.
В первом случае знаком '+' выделяют i -ю строку матрицы С k, а элемент сijk отмечают штрихом. Если на пересечении μ -го выделенного столбца i-й строки матрицы С k расположен Х k -существенный нуль матрицы С k, то знак выделения этого столбца уничтожают, а сам элемент ciμk =0 отмечают звездочкой. Далее просматривают столбец m, отыскивают в нем невыделенный неполный нуль (нули). Если такой нуль имеется, то отмечают его штрихом и анализируют строку, содержащую его. За конечное число шагов процесс выделения Х k -неполных нулей матрицы С k заканчивается одним из трех исходов:
1) найден Х k -неполный нуль в строке і, где 
> 0, тогда переходим ко второму этапу, отметив этот нуль штрихом;
2) все Х k -неполные нули выделены, для каждого из них , а среди невыделенных элементов матрицы С k имеются либо положительные, либо среди дважды выделенных элементов С k (т.е. элементов, расположенных на пересечении выделенных строк и столбцов), отрицательные элементы. В этом случае переходим к третьему этапу;
3) все Х k -неполные нули выделены (для кажого из них dи (k) = 0), все невыделенные элементы С k - отрицательны, а дважды выделенные -положительны. Это означает неразрешимость Т d - задачи.
Второй этап. Он состоит в построении цепочки из нулей матрицы С k, отмеченных штрихами и звездочками. С помощью этой цепочки осуществляют переход от Х k к Х k +1. Итак, пусть первый этап завершился таким образом, что для некоторого невыделенного неполного нуля, расположенного, например, на пересечении строки l 1 и столбца m 1, невязка 
. Этот элемент принимают за начало цепочки из отмеченных нулей матрицы С k. Цепочку строят так.
Движутся по столбцу m 1 матрицы С 0 и находят в нем нуль со звездочкой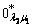 
, далее движутся от него по строке l 1 и находят 
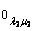и т.д. Процесс построения цепочки, складывающийся из последовательных переходов от нуля со штрихом к нулю со звездочкой по столбцу и от нуля со звездочкой к нулю со штрихом по строке, всегда начинается и заканчивается на нуле со штрихом.
Пусть в результате построения образована цепочка вида
. (3.3.22)
Элементы хij (k+1) матрицы Х k +1 вычисляют по рекуррентной формуле
|
- не входят в цепочку;
если 
(3.3.23)
Параметр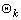 
определяют из соотношения
, (3.3.24)
где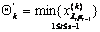 
- минимальный четный по порядку следования элемент цепочки; 
- минимальный резерв до насыщения для нечетных (по порядку следования) элементов цепочки;
- невязкая строки, откуда начинается цепочка,
- невязкая столбца, где цепочка заканчивается.
Если суммарная невязка
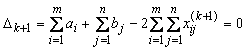
то матрица Х k +1 является решением Т d -задачі, в противном случае переходят к следующей итерации.
Третий этап. На этом этапе производят преобразование матрицы С k в эквивалентную матрицу С k '.
Пусть первый этап закончился вторым исходом. Обозначим минимальный элемент
,
где h ' - минимальный среди невыделенных положительных элементов матрицы С k; h '' - минимальный среди дважды выделенных отрицательных элементов матрицы С k, взятых с обратным знаком. Вычитаем h из элементов матрицы С k, расположенных в невыделенных строках, и прибавляем h к элементам С k, расположенным в выделенных столбцах. Получим матрицу С k '. Если дважды выделенный отрицательный элемент С k становится нулем в С k ', то знак выделения над столбцом уничтожают, а сам элемент отмечают звездочкой. Остальные знаки выделения, а также все отметки нулей переносят из матрицы С k в матрицу С k '.
Далее, снова переходят к первому этапу, заменив С k на С k '. Если первый этап снова завершится вторым исходом, то опять возвращаются к третьему этапу. Циклы, состоящие из первого и третьего этапов, проводят до тех пор, пока последний из них не закончится первым или третьим исходом. При первом исходе переходят ко второму этапу, а при третьем - делают вывод о неразрешимости Т d -задачи из-за несовместимости ее условий.
Пример 3.6. Решить венгерским методом Т d -задачу со следующими условиями
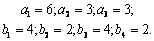
- матрица пропускных способностей коммуникаций.
Предварительный этап. Составляем матрицу С:
.
Затем строим матрицу Х 0 с учетом матрицы D:
.
Будем отмечать одной точкой сверху неполные нули матрицы С k, а двумя точками Х k -полные нули этих матриц. Строки матрицы С k, которым отвечают ненулевые невязки, будем отмечать знаком '´'.
Первая итерация Третий этап
Первый этап Второй этап
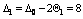
Первая итерация. Первый этап. Знаком '+' выделяем четвертый столбец. Так как матрица С 0 не содержит ни одного Х 0 - неполного нуля, то сразу переходим к третьему состоянию, отыскиваем неполный невыделенный нуль, c 23 и, отметив его штрихом, переходим ко второму этапу. Цепочка, построенная на втором этапе, состоит из одного элемента x 320 . Поэтому
Вторая итерация
|
Третья итерация
Первый этап Третий этап
Второй этап
D3 = 2
Третья итерация состоит из первого и третьего этапов при h = 1, а также из первого и второго этапов, причем цепочка второго этапов, причем цепочка второго этапа содержит лишь один элемент x 312.
Четвертая итерация
Первый и третий этапы
Третий этап Первый этап
Второй этап 
Поскольку суммарная невязка D4=0, то Х 4-оптимальный план. Соответствующее значение целевой функции L min=3.I + 1.4 + 2.2 + 1.4 + 2.1 + 1.3 + 1.2 + 1.1 = 23.
