Решение:
Согласно правилу Шульца-Гарди, теоретически обоснованному Дерягиным и Ландау, порог коагуляции обратно пропорционален заряду противоиона в шестой степени.
Поэтому чем выше заряд катиона - тем ниже порог коагуляции.
AlCl3 (Al+3)
MgCl2 (Mg +2)
KNO3 (K+)
низший порог коагуляции будет у AlCl3, затем чуть больше у MgCl2 и более высокий у KNO3
В три колбы налито по 100 мл золя гидроксида железа. Чтобы вызвать явную коагуляцию золя, потребовалось добавить в первую колбу 10,5 мл 1М раствора КСl, во вторую 62,5 мл 0,01 М раствора Na2SO4 в третью – 37 мл 0,001 М раствора Na3PO4. Вычислите пороги коагуляции электролитов и определите знак заряда частиц золя.
Решение:
Вычисляем пороги коагуляции для каждого из добавляемых электролитов по формуле:
С порKCl = 1*0,0105*1000 =90,9 ммоль/л
0,0105+0.1
С пор Na2SO4 = 0,01*0,0625*1000 =3,84 ммоль/л
0,0625+0,1
С пор Na3PO4 = 0,001*0,037*1000 =0,27 ммоль/л
0,037+0,1
Если частицы заряжены отрицательно, то противоионы (ПОИ) - положительно, и наоборот.
Поэтому при полож. заряде мицелл противоионами служат Cl–, SO4 2– и РО4 3–, а при отриц. заряде мицелл - K+ и Na+.
Согласно правилу Шульце-Гарди, порог коагуляции обратно пропорционален заряду противоиона в шестой степени. Поэтому чем выше заряд ПОИ, тем ниже порог коагуляции. Если бы коагуляция вызывалась K+ и Na+ (при отриц. заряде частиц золя), то в трех сл. был одинаковый порог коагуляции, а в данном сл. они разные, поэтому частицы золя имеют не отриц., а положит. заряд.
Даны пороги коагуляции для следующих электролитов (ммоль/л): СП(KNO3) = 50; СП(Na3PO4)=43; СП(AlCl3)=0,099; СП(MgSO4) = 0,81. Каков заряд частиц – золя?
Решение:
Согласно правилу Шульце-Гарди, порог коагуляции СП обратно пропорционален заряду противоиона (иона коагулянта) в шестой степени. Поэтому чем выше заряд иона коагулянта, тем ниже порог коагуляции.
У KNO3 и Na3PO4 одинаковый заряд катиона (+1), но разный порог коагуляции, поэтому катионы - не коагулянты.
Напротив, в рядуKNO3, Mg(SO4)2, Na3PO4,, AlCl3 растет заряд аниона, и падает порог коагуляции, поэтому ионы-коагулянты - анионы (–), а это возможно, если частицы золя заряжены положительно
Вывод: частицы золя заряжены положительно.
Порог коагуляции электролита для золя Al(OH)3 составляет 0,63 ммоль/л. Какой объем 0,01 М раствора электролита надо добавить к 100 мл золя, чтобы вызвать его явную коагуляцию?
пусть Vэл = Х, тогда
0,63 = 1000 Сэл*Vэл
(Vэл+V золя)
подставляем данные в уравнение:
0,63 = 1000*0,01*х
(х+100)
0,63х+63=10х
х=6,72 мл.
Ответ: Vэл = 6,72 мл.
Определите молярную концентрацию водного раствора глюкозы, если этот раствор при температуре 291 К имеет одинаковое осмотическое давление с раствором, содержащим 0,5 моль/л хлорида кальция, а кажущаяся степень диссоциации соли при указанной температуре равна 65,4%.
Решение:
Для глюкозы росм=CГлRT, для хлорида кальция росм=iCхкRT, где i= 1+альфа(k-1), где альфа - степень диссоциации, k - число ионов, на которое распадается формульная единица CaCl2.
Запишем уравнение диссоциации электролита:
СaCl2 = Сa2+ + 2Cl – n = 3
α= 
, отсюда: i =1+α(n-1)
По условию задачи α = 0,654, тогда:
i = 0,654 (3 – 1) + 1 = 0.654 – 2 + 1 = 1,308 + 1 = 2,308
Pосм. = iCRT = 2,308•0,5•0,082•291 = 27,53 атм.
R = 0,082 л∙атм/град,
Pосм. = Рглюкоз. = СRT
С = 
= 
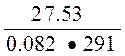= 1,65 моль/л
Ответ: 1,65 моль/
Рассчитайте электрическую проводимость 1М раствора нитрата серебра при температуре 291 К, если расстояние между электродами равно 5 см, а площадь каждого электрода составляет 2 см 2. Молярная электрическая проводимость этого раствора = 94,3 См . см 2. моль –1.
Решение:
Внесистемные единицы (см, см2) необходимо перевести в системные (м, м2),
тогда S=2*2*10-4 м2 = 0,4.10-3 м2; L = 5см=5*10-2м.
Найдем электропроводность р-ра: χ= ήV *С
χ =L/S, подставляя значения, получаем:
ήV = 1000 * L/S = 1000*5*10-2 / 0,4.10-3 = 125 см2/моль
С 1000
Ответ: см2/моль..
Для гальванического элемента(-) Ag | Zn | ZnCl2 | AgCl(т), Ag (+),mZnCl2 = 0,555, используя стандартные электродные потенциалы 0(Zn 2+/Zn) = – 0,763 B; 0(AgCl/Ag,Cl –) = 0,222 В, напишите уравнения катодного и анодного процессов и суммарное уравнение реакции. Вычислите при температуре 273 К стандартную энтальпию r H0273, количество теплоты Qобр, выделяющееся при обратимом протекании реакции в гальваническом элементе, и стандартную ЭДС Е0, если при 273 К Е = 1,125 В; = – 4. 10 –4 В . К –1.
Решение:
Т.к. стандартный электродный потенциал Е⁰ (AgCl/Ag) больше станд. эл. потенциала Е⁰ (Zn/ZnCl2), то на серебряном электроде идет процесс восстановления – это катод, а на цинковом электроде – процесс окисления, это анод.
Катод: Ag + +e = Ag⁰;
Анод: Zn⁰ -2е =Zn +2
В основе работы гальванического элемента лежит реакция:
Zn + 2AgCl= ZnCl2 + 2Ag.
Zn⁰ +2Ag+ =Zn+2 + 2Ag⁰
Вычислим стандартную ЭДС:
Е=φк – φа = 0,222 В –(-0,763 B)=0,985В.
Рассчитаем изменение стандартной энергии Гиббса ΔrG273 токообразующей реакции:
∆G= -nFE = dH + TdS =-2* 23062*1,125 = -46816 ккал
Далее рассчитаем энтропию образования ZnCl2 + 2Ag:
∆S = nF(dE/dT) = -2*23062*4,*10-4 = -18.5 кал/град
Находим стандартную энтальпию r H0273 образования ZnCl2 + 2Ag:
dH = dG + TdS = -46816 - 273*18,5 = -51866,5 кал
Определяем количество теплоты Qобр, выделяющееся при обратимом протекании реакции в гальваническом элементе:
dQ = -dH=-(-51866,5) = 51866,5кал.
