Коэффициент сопротивления рассчитывается по формуле:
Сх.мод (α) = Сх.проф. (α) + Сх.доб.+Сх.инд. (Су (α))
Добавочное сопротивление составляет сопротивление фюзеляжа и сопротивление горизонтального и вертикального оперения. Площади оперения и крыла определим по чертежу.
Сх.доб. = (Сх.доб.ф. + Сх.доб.го.. + Сх.доб.во.)/ Sкр
Сх.доб.ф. = Sф·Сф = 0,00289 м 2·0,25 = 0,0007225;
Сх.доб.го. = Sоп·Соп = 0,05068 м 2·0,059 = 0,00299012;
Сх.доб.во. = Sоп·Соп = 0,00114 м 2·0,4 = 0,000456;
Сх.доб. = (0,0007225+0,00299012+0,000456)/0,288 = 0,014457
Индуктивное сопротивление находим из выражения:
Сх.инд. (Су (α)) = Су (α)2 / (π·λ) = 0,1133· Су (α)2
Рассчитаем поправку Δα для коэффициента подъемной силы:
Δα = Су (α)·57,3/(π·λ) = 6.4921· Су (α)
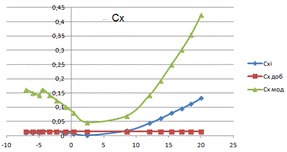Строим в Excel зависимости Сх и Су с учетом удлинения крыла и добавочных сопротивлений:
Рис.7. График зависимости Сy(α) Рис.8. График зависимости Сx(α)
Рассчитаем зависимость положения центра давления от угла атаки в долях САХ:
Са (α) = Сm (α)/ Су (α)
Рис.9. График зависимости Сa(α)
Нахождение центра масс и момента инерции ЛА
Разбиваем самолет на конструктивные элементы, прикидываем массу каждого элемента и находим координаты их центров масс (см. рис.2., ЦМ обозначены синим цветом). Данные сводим в таблицу, в которой указаны:
1) Объем элементов (S b l)
2) Плотность бальзы (ϒ)
3) Масса элементов самолета (m)
4) Координаты центра масс (Х и Y)
5) Расстояние ЦМ элементов от ЦМ самолёта (Х-Хс и Y-Yc)
| S | l | ϒ | m | X | Y | Х-Хс | Y-Yc | |
| Фюзеляж | 0,001659717 | 1,27 | 0,199166074 | 89,79790595 | -0,60555 | |||
| 0,0008 | 0,22 | 0,02112 | ||||||
| Крыло | 0,28835 | 0,025 | 0,032439375 | -87,2020941 | 66,39445 | |||
| Стабил. | 0,0628884 | 0,005 | 0,001257768 | 819,7979059 | 1,394446 | |||
| Верт.О | 0,01445 | 0,01 | 0,01734 | 932,7979059 | 25,39445 | |||
| 0,00465 | 0,005 | 0,00279 | -28 | 939,7979059 | -43,6056 | |||
| Винт | 0,05 | -275,202094 | -15,6056 | |||||
| Мотор | 0,1 | -230,202094 | -15,6056 |
Центр масс самолета определяем по приведенной формуле
, где 
- масса i-ого тела, 
- радиус-вектор, определяющий положение тела, 
– масса тела.
Рассчитаем момент инерции самолета относительно центра масс:
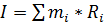, где - масса i-ого тела, 
– расстояние между ЦМ элементов и ЦМ самолёта
Определим расстояния от точек приложения сил до общего центра масс:
тяга винта: по оси Х – 0,259 м, по оси У – 0,02 м;
аэродинамические силы крыльев меняются с изменением центра давления (на САХ)
аэродинамические силы ГО: оси Х - 0,85 м, по оси У – 0,002 м;
Модель воздушного винта и центровка модели
Используем английский тип винта
диаметр винта: 0,184м
число лопастей: 2
число оборотов: 10500 об/мин = 175 об/с
Рассчитываем относительную поступь винта для режима полета:
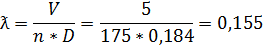
Тяга винта определяется формулой:
, где α - коэффициент тяги винта.
Коэффициент тяги винта выбирается для каждого типа винта и угла установки лопастей. По характеристикам винта подбираем ближайший (в книге Кравеца) и оцифровываем для него график зависимости α(λ):
Рис.10. Зависимость тяги винта от коэффициента α.
