Таблица 2.4 – Основные законы и формулы
| Физические законы, переменные | Формулы |
| Внутренняя энергия U газа массой m; i – число степеней свободы; μ – молярная масса газа; R - универсальная газовая постоянная; Т - температура | 
|
| Изменение внутренней энергии dU идеального газа при изменении температуры на величину dT | 
|
| Элементарная работапо расширению и сжатию газа: где р – давление газа, dV – изменение объема газа. | 
|
| Полная работа | 
|
| Работа газа при изотермическом расширении | 
|
| Работа газа при изобарном расширении | 
|
| Работа газа при изохорном процессе: | 
|
| Количество теплоты Q, необходимой для нагревания тела массой m; c – удельная теплоёмкость | 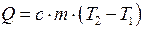
|
| Первый закон термодинамики: где Q – количество теплоты, подводимое к системе; ΔU – изменение внутренней энергии; А – работа, совершаемая системой против внешних сил. | 
|
| Удельная теплоемкость: | 
|
| Молярная теплоемкость: 1) молярная теплоемкость изохорная; 2) молярная теплоемкость изобарная где R - универсальная газовая постоянная, i – число степеней свободы |  ;
1) ;
1)  ;
2) ;
2)  ; ;
|
| Уравнение Майера: | 
|
| Уравнение политропы: | 
|
| Показатель политропы: | 
|
| Работа газа при политропном процессе: | 
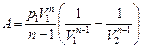
|
| Показатель адиабаты (коэффициент Пуассона): | 
|
| Уравнение адиабаты: | 
|
| Коэффициент полезного действия η тепловой машины; Q1 – теплота, передаваемая рабочему телу нагревателем; Q2 – теплота, передаваемая рабочим телом холодильнику | 
|
| Коэффициент полезного действия ηк идеальной тепловой машины, работающей по циклу Карно; Т1 - температура нагревателя, и Т2 - температура холодильника | 
|
| Изменение энтропии при переходе из состояния 1 в состояние 2: где dQ – количество теплоты, Т – термодинамическая температура. | 
|
Примеры решения задач
1. Внутренняя энергия некоторого количества азота при температуре 20º равна 4·103 Дж. Определить массу газа.
Дано:
μ2(N2)=24·10-3кг/моль,
t = 20ºC, Т = 273+20=293 К
U = 4·103 Дж.
Найти:
m–?
Решение
Внутренняя энергия газа
 ,
,
где m – масса газа, μ – молярная масса газа, R – универсальная газовая постоянная, T – термодинамическая температура, i – число степеней свободы молекулы, так как азот двухатомный, то i =5, тогда
 ,
,
 ,
,

Ответ:  .
.
2. Одноатомный газ был нагрет при постоянном давлении р = 90 кПа. В результате его объем увеличился на DV = 2 см2. Найти: 1) совершенную газом работу, 2) приращение внутренней энергии DU газа, 3) количество теплоты Q, сообщенное газу.
Дано:
р = 90 кПа = 90·103Па,
DV = 2 см3 = 2·10-6м3,
p=const,
i = 3.
Найти:
А –?
DU–?
Q–?
Решение
При изобарном процессе Р = const первый закон термодинамики можно записать в виде:
 ,
,
где А – работа,
 ,
,
р – давление газа, DV – изменение объема газа.
 ,
,

ΔU – изменение внутренней энергии газа, вычисляется по формуле:
 ,
,
где i – показатель степени свободы молекулы, i = 3, так как гелий одноатомный газ, R –универсальная газовая постоянная, μ – молярная масса гелия. Из уравнения Менделеева – Клапейрона
 ,
,
тогда
 ,
,


Количество теплоты
 .
.
Ответ:  ,
, 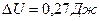 ,
, 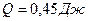 .
.
3.Газ расширяясь изобарно при давлении 2.105 Па, совершает работу 200 Дж. Определить первоначальный объем газа, если конечный объем равен 2,5 л.
Дано:
р=2.105 Па,
А = 200 Дж,
p=const,
V2 = 2,5 л = 2,5·10-3м3.
Найти:
V1–?
Решение
Работа при изобарном процессе вычисляется по формуле:
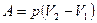 ,
,
где р – давление газа, V1 – начальный объем, V2 – конечный объем газа, отсюда
 ,
,
 ,
,

Ответ: 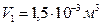 .
.
4. Вычислить удельные теплоемкости при постоянном объеме cv и при постоянном давлении ср неона и водорода, принимая эти газы за идеальные.
Дано:
i(Ne) = 3,
i(H2) = 5
μ(Ne) = 20·10-3 кг/моль,
μ(H2) = 2·10-3 кг/моль,
Найти:
cv –?
ср –?
Решение
Удельные теплоемкости идеальных газов выражаются формулами
 ,
,  ,
,
где i – число степеней свободы молекулы газа; μ – молярная масса. Для неона (одноатомный газ) i = 3 и μ = 20·10-3 кг/моль.
Произведем вычисления:
 ,
,
 .
.
Для водорода (двухатомный газ) i = 5 и μ = 2·10-3 кг/моль. Тогда:
 ,
,
 .
.
Ответ: для неона:  ,
, 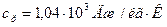 ; для водорода:
; для водорода: 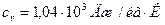 ,
,  .
.
5. Кислород массой m = 2 кг занимает объем V1 = 1 м3 и находится под давлением Р1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3 м3, а затем при постоянном объеме до давления Рз = 0,5 МПа. Найти изменение ΔU внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
Дано:
m = 2 кг,
V1 = 1 м3,
Р1 = 0,2 МПа = 0,2·106Па,
V2 = 3 м3,
Рз = 0,5 МПа = 0,5·106Па
Найти:
ΔU –?
А –?
Q –?
Решение
Изменение внутренней энергии газа равно:
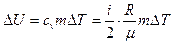 ,
,
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5);  – разность температур газа в конечном (третьем) и начальном состояниях.
– разность температур газа в конечном (третьем) и начальном состояниях.
Начальную и конечную температуру газа найдем из уравнения состояния идеального газа: 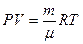 , откуда
, откуда
 .
.
Работа расширения газа при постоянном давлении выражается формулой:
 .
.
Работа газа, нагреваемого при постоянном объеме, равна нулю:  . Следовательно, полная работа, совершаемая газом,
. Следовательно, полная работа, совершаемая газом,  .
.
Согласно первому началу термодинамики, количество теплоты Q,переданное газу, равна сумме изменения внутренней энергии ΔU и работы А:
 .
.
Произведем вычисления, учтя, что для кислорода μ = 32·10-3 кг/моль:
 ,
,
 ,
,
 .
.
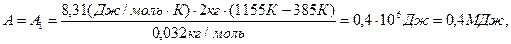
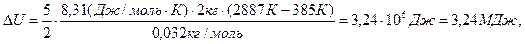
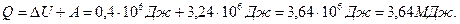
Ответ: 
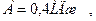

 |
6. В цилиндре под поршнем находится водород массой m = 0,02 кг при температуре Т1 = 300 К. Водород сначала расширился адиабатно, увеличив свой объем в n1 = 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n2 = 5 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразить процесс графически.
Дано:
m = 0,02 кг,
Т1 = 300 К,
n1 = 5 раз,
n2 = 5 раз.
Найти:
Т2 –?
А1 –?
А2 –?
Решение
Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением:
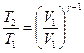 или
или  ,
,
где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме;  . Отсюда получаем следующее выражение для конечной температуры:
. Отсюда получаем следующее выражение для конечной температуры:
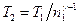 .
.
Работа А1 газа при адиабатном расширении может быть определена по формуле:
 ,
,
где Cv – молярная теплоемкость газа при постоянном объеме. Работа А2 газа при изотермическом процессе может быть выражена в виде:
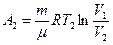 или
или  ,
,
где  .
.
Найдем числовые значения искомых величин, учитывая, что для водорода как двухатомного газа γ = 1,4, i = 5 и μ = 2·10-3 кг/моль:
 .
.
 ,
,
 .
.
Знак «минус» показывает, что при сжатии работа газа совершается над газом внешними силами.
График процесса приведен на рисунке

Ответ:  ,
,  ,
, 
7. 10 г кислорода находятся под давлением 3 бар при температуре 10о С. После нагревания при постоянном давлении газ занял объем 10 л. Найти: 1) количество тепла, полученного газом; 2) энергию теплового движения газа до и после нагревания.
Дано:
m=10г =10-2кг,
р=3 бар =3·105Па,
V =10 л = 10-2м3.
Найти:
ΔQ –?
W1 –?
W2 –?
Решение
1 Количество тепла, полученного газом, найдем по формуле:
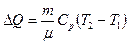 .
.
Чтобы Т2, запишем уравнение состояния газа до нагревания: 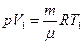 и после нагревания:
и после нагревания: 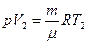 . Из этих уравнений получаем:
. Из этих уравнений получаем:  , где
, где 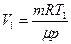 . Следовательно,
. Следовательно,
 .
.
Таким образом,  ,
,
 .
.
2 Энергия газа до нагревания может быть найдена по формуле:
 .
.
Энергия газа после нагревания:
.
Ответ:  ,
,  ,
,  .
.
8. В закрытом сосуде объемом 10 л находится воздух при давлении 105 Па. Какое количество тепла надо сообщить воздуху, чтобы повысит давление до 5·105 Па?
Дано:
V = 10л =10-2м3,
р1 = 105Па,
р2 = 5·105Па.
Найти:
Q –?
Решение
Количество теплоты, которое необходимо сообщить воздуху, находится по формуле:
 .
.
Чтобы найти ΔТ, запишем уравнение состояния газа до и после нагревания. Так как  , то:
, то:
 и
и  .
.
Отнимая из первого уравнения второе, получим:
 или
или 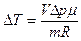 .
.
Теплоемкость воздуха при постоянном объеме определяется формулой:  , где
, где 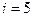 - число степеней свободы для двухатомного газа (воздух принимается за двухатомный газ). Подставляя два последних уравнения в первую формулу, получим:
- число степеней свободы для двухатомного газа (воздух принимается за двухатомный газ). Подставляя два последних уравнения в первую формулу, получим:
 ,
,
 .
.
Ответ: 
9. Какой должна быть температура нагревателя, для того чтобы в принципе стало возможным достижение значения КПД тепловой машины 80%, если температура холодильника 270С?
Дано:
η=80%,
Т2 = 270С.
Найти:
Т1 –?
Решение
КПД идеальной тепловой машины:
 , (1)
, (1)
где Т1 – температура нагревателя, Т2 – температура холодильника.
Преобразуем выражение (1)
 .,
.,
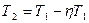 ,
,
 ,
,
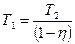 ,
,
Т2 = 27+273=300К,
 .
.
Ответ:  .
.
10.Идеальная тепловая машина работает по циклу Карно. Определить к.п.д. цикла, если известно, что за один цикл была произведена работа, равная 3000 Дж, и холодильнику было передано 1,35·104 Дж теплоты.
Дано:
А = 3000 Дж,
Q2 = 1,35·104 Дж.
Найти:
η –?
Решение
КПД тепловой машины
 , (1)
, (1)
где А – совершаемая работа, Q1 – количество теплоты полученное от нагревателя.
Работа равна:
 ,
,
где Q2 – количество теплоты, преданное холодильнику, отсюда
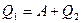 ,
,
тогда
 ,
,
 .
.
Ответ:  .
.
11. В процессе работы тепловой машины за некоторое время рабочим телом было получено от нагревателя количество теплоты Q1=1,5·106Дж, передано холодильнику Q2=-1,2·106Дж. Вычислите КПД машины и сравните его с максимально возможным КПД машины, если температура нагревателя и холодильника соответственно равны 2500С и 300С.
Дано:
Q1=1,5·106Дж,
Q2=-1,2·106Дж,
Т1 = 2500С,
Т2= 300С.
Найти:
η1 –?
η2 –?
Решение
КПД тепловой машины
 ,
,
где Q1 – количество теплоты, полученное от нагревателя, Q2 – количество теплоты, преданное холодильнику,
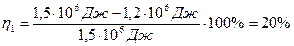
КПД идеальной тепловой машины:
 ,
,
где Т1 – температура нагревателя, Т2 – температура холодильника.
Т1 = 250+273=523К, Т2 = 30+273=303К, тогда
 .
.
Ответ:  ,
, 






