Практическое занятие №3
Тема: Молекулярно - кинетическая теория идеальных газов
Цель: обобщение и систематизация знаний, умений по данной теме; формирование практических навыков при решении задач; развитие интереса к изучению физики
Краткие теоретические сведения
Таблица 2.3 – Основные законы и формулы
| Физические законы переменные | Формулы |
| Число ν молей вещества, m – масса, μ – молярная масса |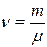 
|
| Масса m0 одной молекулы газа, NA – число Авогадро | 
|
| Число молекул N в некоторой массе т газа | 
|
| Закон Дальтона для смеси газов: где р – давление смеси газов; рn – давление n – го компонента смеси (парциальное давление); n – число компонентов смеси. |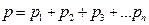 
|
Основное уравнение молекулярно – кинетической теории газов:
где р – давление газа; m0 – масса одной молекулы;  - концентрация молекул, число молекул в единице объема, 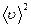 - средняя квадратичная скорость молекул
| 
|
| Средняя кинетическая энергия Ек теплового движения молекул газа; i – число степеней свободы, k – постоянная Больцмана | 
|
| Формула связывающая давление газа и среднюю кинетическую энергию поступательного движения молекул: |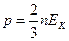 
|
| Уравнение Менделеева – Клапейрона, р – давление, V – объём, R – универсальная газовая постоянная, Т - температура |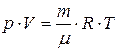 
|
| Уравнение Клапейрона(уравнение состояния газа): | 
|
| Изопроцессы: 1)изотермический процесс m = const, Т= const; 2) изобарный процесс m = const,р= const; 3) изохорный процесс m = const,V= const; | 1)  ;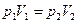
2)  ;
3) 
|
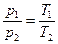
| Зависимость давления газа от концентрации и температуры: |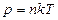 
|
| Скорости молекул: 1) средняя квадратичная скорость молекул; 2) наиболее вероятная скорость молекул; 3) средняя арифметическая скорость молекул. | 1)  ;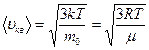
2)  ;
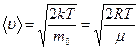3) 
|
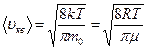
| Средняя длина свободного пробега молекулы где d – эффективный диаметр молекул водорода; n – концентрация молекул |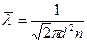 
|
Среднее число столкновений за единицу времени,
где 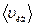 - средняя арифметическая скорость молекул,  - средняя длина свободного пробега молекулы
| 
|
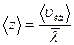
Примеры решения задач
1.Найти массу атомов: 1) водорода; 2) гелия. 3) молекулы СО2
Дано:
1) водород (Н2)
2) гелия (Не)
3) молекулы СО2
Найти:
1) m0 (Н2) –?,
2) m0 (Не) –?,
3) m0 (СО2) –?
Решение
Молярная масса газа
,
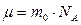где m0 – масса атома, NA – число Авогадро, отсюда
.
Пользуясь таблицей Менделеева, определим молярные массы вещества
,
,
.
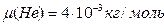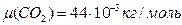Вычислим
,
,
.
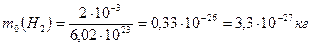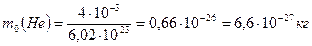Ответ: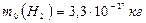 
, 
, 
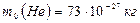
2. Какова средняя кинетическая энергия молекулы газа, если его давление равно 5.104 Па, а в объеме 12 л содержится 6.1024 молекул?
Дано:
р=5.104 Па
V=12 л=12·10-3м3
N=6·1024
Найти:
Ek=?
Решение:
Из основного уравнения молекулярно-кинетической теории
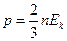
где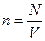 
- концентрация. Тогда
,
,
,
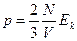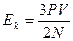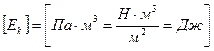Дж
Ответ: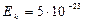 
Дж
3 Определите массу газа, объем которого 5 м3, давление 3 атм, а средняя квадратичная скорость молекул 1500 м/с.
Дано:
V=5 м3,
Р=3 атм = 3·105Па,
.
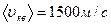Найти:
m–?
Решение
Средняя квадратичная скорость молекул
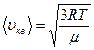, (1)
где R – универсальная газовая постоянная, T – термодинамическая температура, μ – молярная масса газа.
Возведем к квадрат уравнение (1) получим:
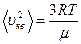. (2)
Изуравнение Менделеева – Клапейрона
,
или
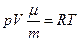(3)
Подставим уравнение (3) в (2)
,
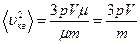отсюда
,
,
Ответ: 
.
3. Газ при температуре t=150С и давлении р= 200 кПа имеет плотность ρ = 0,34 кг/м3. Найти молярную массу μ газа.
Дано:
t=150С, Т=273+15=288 К,
р= 200 кПа=2·105Па,
ρ = 0,34 кг/м3.
Найти:
μ –?
Решение
Из уравнения Менделеева – Клапейрона
,
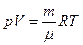где V – объем газа, R – универсальная газовая постоянная,
.
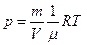Плотность газа
,
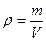Тогда
,
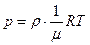отсюда
,
,
.
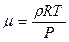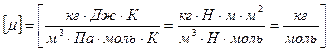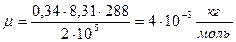Ответ: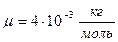 
4. Какой объем занимает смесь азота массой 2 кг и гелия массой 1 кг при нормальных условиях. Чему равна молярная масса смеси?
Дано:
m1 = 2 кг,
m2 = 1 кг,
Т = 273К,
р = 105Па,
μ1(N2)=28·10-3кг/моль,
μ2(Не) = 4·10-3кг/моль.
Найти:
V–?
μ–?
Решение
Объем смеси газов
,
где V1 – объем азота, V2 – объем гелия.
Объемы газов найдем из уравнения Менделеева – Клапейрона:
,
,
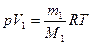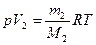отсюда
,
,
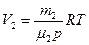где R – универсальная газовая постоянная, р – давление газа, Т – термодинамическая температура, тогда
,
,
.
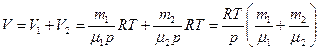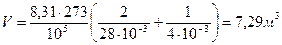Молярная масса смеси μ есть отношение массы смеси m к количеству вещества смеси ν,т.е
.
Масса смеси равна сумме масс компонентов смеси m=m1+m2. Количество вещества смеси равно сумме количеств вещества компонентов. Подставив в формулу , выражения m=m1+m2 и 
, получим
,
,
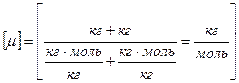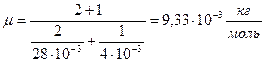
Ответ: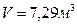 
, 
.
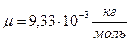5. Баллон ёмкостью 10 л содержит водород массой 1 г. Найти среднюю длину свободного пробега молекул.
Дано:
Н2
d =0,28·10-9м
V=10 л=0,01м3
m= 1 г=10-3кг
Найти:
λ=?
Решение:
Средняя длина свободного пробега молекулы
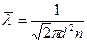, (1)
где d – эффективный диаметр молекул водорода; n – концентрация молекул.
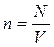
Так как
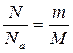
М=0,002 кг/моль – молярная масса водорода, Na=6,022·1023 – число Авогадро.
Тогда,
Вычислим:
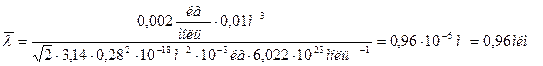
Ответ: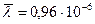 
м=0,96мкм
6. Определить среднее число соударений в секунду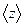 
и длину свободного пробега молекул водорода при температуре t = 270С и давлении Р = 1·10-3 мм.рт.ст.
Дано:
t = 270С,
Р = 1·10-3 мм.рт.ст. = 133,3·10-3 Па,
d = 0,23·10-9 м,
М(Н2) = 2·10-3 кг/моль
Найти:
–?,
–?
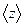Решение
Средняя длина свободного пробега молекулы
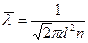, (1)
где d – эффективный диаметр молекул водорода; n – концентрация молекул.
Из основного уравнения молекулярно – кинетической теории
,
имеем
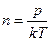, (2)
где p – давление, k – постоянная Больцмана, T – термодинамическая температур.,
Т = 273+27 = 300 К
Тогда, с учетом (2), выражение (1) можно записать в виде
.
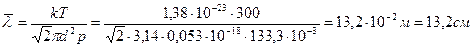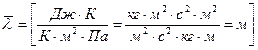
С другой стороны длина свободного пробега
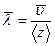, (3)
где 
– средняя арифметическая скорость молекул, 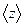– среднее число столкновений за единицу времени,
Из выражения (3)
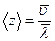. (4)
Средняя арифметическая скорость вычисляется по формуле
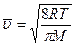, (5)
где R – универсальная газовая постоянная, T– термодинамическая температура, M – молярная масса водорода.
Таким образом, с учетом (5) запишем выражение (4)
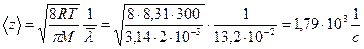
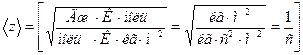
Ответ: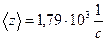 
; 
Задачи для решения на занятии
1. Определить молярную массу ацетилена (С2Н2). (Ответ: 2,6·10-2 кг/моль)
2. Сколько молекул воды содержится в капле массой 0,2 г? (Ответ: 6,7·1021)
3. Сколько молекул газа содержится в колбе вместимостью 500 см3 при нормальных условиях? (Ответ: 1,34·1022)
4. Сколько молекул содержится при нормальных условиях в 1 кг кислорода? Плотность кислорода при нормальных условиях приять равной 1,43 кг/м3. (Ответ: 1,9·1025)
6. Определите давление водорода, если средняя квадратичная скорость его молекул 800 м/с, а его плотность 2,4 кг/м3. (Ответ: 0,512 МПа).
7.Найти температуру газа при давлении 100 кПа и концентрации молекул 1025м-3. (Ответ: 724 0К)
8.Найти среднюю квадратичную скорость молекул воздуха при температуре 170С. молярная масса воздуха 0,029 кг/моль. (Ответ: 500 м/с)
9. Найти среднюю длину свободного пробега молекул углекислого газа при температуре 1000С и давлении 13,3 Па. Диаметр молекул углекислого газа 0,32 нм.(Ответ:850 мкм)
10. Найти среднее число столкновений в единицу времени молекул углекислого газа при температуре 1000С, если средняя длина свободного пробега 870 мкм. (Ответ: 4,87·105 с-1)
Вопросы для самоконтроля
1. Сформулируйте основные положения молекулярно – кинетической теории.
2. Что такое относительная молекулярная масса?
3. Что называют количеством вещества? Единица измерения.
4. Каков физический смысл постоянной Авогадро?
5. В чем измеряется молярная масса?
6. Какой газ называется идеальным?
7. Что такое давление? Чем оно обусловлено?
8. Что называется термодинамическим процессом? изопроцессом?
9. Сформулируйте законы Бойля – Мариотта, Гей – Люссака, Шарля.
10. Какая температура называется термодинамической?
11. Какой физический смысл имеет газовая постоянная и постоянная Больцмана?
12. Какова связь между кинетической энергией поступательного движения молекул газа и его термодинамической температурой?.
13. Какую величину называют длиной свободного пробега молекул?
