Практическое занятие № 8
Явления переноса. Реальные газы, жидкости, твердые тела
Цель: Обобщение и закрепление теоретического материала по теме «Реальные газы и особенности жидкого и твердого состояний вещества» и рассмотрение решения задач по данной теме.
Требования к исходному уровню знаний и умений
Знать определения следующих физических понятий:
• Явления переноса;
• Теплопроводность;
• Диффузия;
• Внутреннее трение;
• Молекулярное давление (или внутреннее);
• Смачивание (несмачивание);
• Избыточное (добавочное) давление;
• Капиллярность;
• Испарение, конденсация, плавление и кристаллизация;
• Фазовые переходы I и II рода;
• Тройная точка.
Знать определения следующих физических величин, уметь записать формулы, которыми они определяются, указать единицы измерения и значения.
• Теплопроводность;
• Диффузия (коэффициент диффузии);
• Динамическая вязкость;
• Поверхностная энергия;
• Краевой угол;
Знать формулировку, уметь записать формулы, определяющие следующие физические законы:
• Закон Фурье;
• Закон Фика;
• Закон Ньютона.
Уметь записать уравнение Ван-дер-Ваальса (уравнение состояния реальных газов) для 1 моль газа и для произвольного количества вещества.
Уметь записать и пояснить формулу Лапласа.
Уметь изобразить графически изотермы Ван-дер-Ваальса и указать критические параметры.
Уметь изобразить графически диаграмму состояния фазовых превращений.
Сведения из теории
Импульс, переносимый молекулами из одного слоя газа в другой через элемент поверхности площадью D S за время d t,
 ,
,
где h – динамическая вязкость газа; d v /d x – поперечный градиент скорости течения его слоев.
Динамическая вязкость

где r – плотность газа (жидкости).
Закон Ньютона для силы внутреннего трения (вязкости) между слоями площадью D S
 .
.
Закон теплопроводности Фурье

где D Q – теплота, прошедшая посредством теплопроводности через площадку S за время D t; d T /d x – градиент температуры; l – теплопроводность, для газов

с v – удельная теплоёмкость газа при постоянном объёме; r – плотность газа; á v ñ и á l ñ – средняя арифметическая скорость и средняя длина свободного пробега молекул.
Закон диффузии Фика

где D m – масса вещества, переносимая в результате диффузии через поверхность площадью S за время D t; d r /d х – градиент плотности; D – коэффициент диффузии; для газов
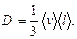
Уравнение Ван-дер-Ваальса

где р – давление; m – масса; m – молярная масса; a и b – постоянные Ван-дер-Ваальса; V – объем; Т – термодинамическая температура.
Связь критических параметров – объема, давления и температуры газа – с постоянными Ван-дер-Ваальса:

Коэффициент поверхностного натяжения
 ,
,
где F – сила поверхностного натяжения, действующая на контур длиной  , ограничивающий поверхность жидкости.
, ограничивающий поверхность жидкости.
При изотермическом увеличении площади поверхности плёнки жидкости на D S совершается работа
А = a D S.
Добавочное давление D р, вызванное кривизной поверхности жидкости, выражается формулой Лапласа

где R 1 и R 2 – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
В случае сферической поверхности
D р = 2 a / R.
Высота поднятия жидкости в капиллярной трубке

где q – краевой угол; r – плотность жидкости; g – ускорение свободного падения; r – радиус трубки.
Высота поднятия жидкости в зазоре между двумя близкими и параллельными плоскостями

где d – расстояние между плоскостями.
Задания для практической части занятия
1. Давление разреженного газа в рентгеновской трубке при температуре 17°С равно 130 мкПа. Можно ли вести разговор о высоком вакууме, если характерный размер l0 (расстояние между катом и анодом трубки) составляет 50 мм? Эффективный диаметр) воздуха примите равным 0,27 нм.
2. Определите во сколько раз отличаются коэффициенты динамической вязкости η углекислого газа и азота, если оба газа находятся при одинаковой температуре и одном и том же давлении. Эффективные диаметры молекул этих газов равны.
3. Определите коэффициент теплопроводности λ азота, если коэффициент динамической вязкости η для него при тех же условиях равен 10 мкПа·с.
4. Определите коэффициент диффузии D кислорода при нормальных условиях. Эффективный диаметр молекул кислорода примите равным 0,36 нм.
5. В цилиндре под поршнем находится хлор массой m = 20 г. определить изменение ΔU внутренней энергии хлора при изотермическом расширении его от V 1 = 200 см3 до V 2 = 500 см3 (постоянная Ван-дер-Ваальса а = 0,65 Н·м4/моль2).
6. При определении силы поверхностного натяжения капельным методом число капель глицерина, вытекающего из капилляра, составляет n = 50. Общая масса глицерина m = 1 г, а диаметр шейки капли в момент отрыва d = 1 мм. Определите поверхностное натяжение σ глицерина.
7. Давление воздуха внутри мыльного пузыря на Δ р = 200 Па больше атмосферного. Определите диаметр d пузыря. Поверхностное натяжение мыльного раствора σ = 40 мН/м.
8. Воздушный пузырек диаметром d = 0,02 мм находится на глубине h = 25 см под поверхностью воды. Определите давление воздуха в этом пузырьке. Атмосферное давление примите нормальным. Поверхностное натяжение воды σ = 73 мН/м, а ее плотность ρ = 1 г/см3.
9. Определите коэффициент диффузии D кислорода при нормальных условиях, если коэффициент теплопроводности λ = 8,25 мВт/(м·К).
10. Пространство между двумя параллельными пластинами площадью 150 см2 каждая, находящимися на расстоянии 5 мм друг от друга, заполнено кислородом. Одна пластина поддерживается при температуре 170С, а другая – при температуре 270С. Определите количество теплоты, прошедшее за 5 мин посредством теплопроводности от одной пластины к другой. Кислород находится при нормальных условиях. Эффективный диаметр молекул кислорода считать 0,36 нм.
11. Определите массу азота, прошедшего вследствие диффузии через площадку 50 см2 за 20 с, если градиент плотности в направлении, перпендикулярном площадке, равен 1 кг/м4. Температура азота 290 К, а средняя длина свободного пробега его молекул равна 1 мкм.
12. Пространство между двумя большими параллельными пластинами, расстояние между которыми равно 5 мм, заполнено гелием. Температура одной пластины поддерживается равной 290 К, другой – 310К. Вычислить плотность теплового потока q. Расчеты выполнить для двух случаев, когда давление гелия равно: 1) 0,1 МПа; 2) 1МПа.
13. Углекислый газ массой 10г находится в сосуде вместимостью V = 1л. Принимая поправки Ван – дер – Вальса а = 0,36 Н·м4/моль2 и b = 4,28·10-5м3/моль, определите:1) собственный объем V' молекул газа; 2) внутреннее давление р' газа.
14. Азот массой 1,4 кг находится при температуре 300К в сосуде вместимостью 40 л. Определите давление газа, если: 1) газ реальный; 2) газ идеальный. Поправки Ван – дер – Вальса а = 0,135 Н·м4/моль2 и b = 3,86·10-5м3/моль соответственно.
15. Кислород (v = 2 моль) занимает объем V 1 = 1л. Определите изменение температуры кислорода, если он адиабатно расширяется в вакуум до объема V 2 = 10л (поправка Ван – дер – Вальса а = 0,136 Н·м4/моль2).
Ответы
№1. Вакуум высокий.
№2. η 1/ η 2 = 1,25.
№3. λ = 7,42 мВт/(м·К).
№4. D = 9,18·10-6 м2/с.
№5. Δ U = 155 Дж.
№6. σ = 62,5 мН/м.
№7. d = 1,6 мм.
№8. р = 118 кПа.
№9. D = 8,89·10-6 м2/с.
№10. Q = 76,4 кДж
№11. m = 15,6 мг.
№12. 1) q1 = 196 Вт/м2; 2) q2 = 35 Вт/м2.
№13. 1) V' = 2,43 см3; 2) р' = 18,6
№14. 1) р1 = 3,06 МПа; 2) р2 = 3,12 МПа.
№15 Т2 – T1 = -11,8.






