Практическое занятие № 4
Вращательное движение твердого тела
Цель: Обобщение и закрепление теоретического материала по теме «Вращательное движение твердого тела» и рассмотрение решения задач по данной теме.
Требования к исходному уровню знаний и умений
Знать определения следующих физических понятий:
Ø Твердое тело;
Ø Вращательное движение;
Знать определения следующих физических величин, уметь записать формулы, которыми они определяются, указать единицы измерения и направление (для векторных физических величин):
Ø Момент импульса материальной точки относительно неподвижной точки
Ø Момент импульса материальной точки относительно неподвижной оси;
Ø Момент силы относительно неподвижной точки;
Ø Момент силы относительно неподвижной оси;
Ø Плечо силы;
Ø Главный момент внешних сил относительно точки;
Ø Момент импульса системы;
Ø Момент инерции;
Ø Момент инерции материальной точки;
Ø Момент инерции механической системы;
Ø Момент инерции твердого тела;
Ø Кинетическая энергия вращающегося тела;
Ø Полная кинетическая энергия катящегося тела;
Ø Работа силы при вращательном движении тела
Знать формулировку, уметь записать формулы, определяющие следующие физические законы:
Ø Основной закон динамики вращательного движения твердого тела относительно точки;
Ø Закон сохранения момента импульса;
Ø Основной закон динамики вращательного движения твердого тела относительно неподвижной оси.
Знать формулировку, уметь записать формулу теоремы Штейнера.
Момент инерции для некоторых тел
Таблица 1.
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | 
|
| Сплошной цилиндр или диск радиусом R | Ось симметрии

| 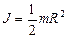
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину
| 
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец

| 
|
Шар радиусом R Ось проходит через центр шара
Таблица 2
Поступательное движение Вращательное движение
Масса m Момент инерции J
Скорость
Угловая скорость
Ускорение
Угловое ускорение
Сила
Момент силы Mz или
Импульс
Момент импульса
Основное уравнение динамики
Основное уравнение динамики
Работа dA = Fsds Работа dA = Mzdφ
Кинетическая энергия
Кинетическая энергия
Задания для практической части занятия
- Определите момент инерции тонкого однородного стержня длиной l = 1м и массой m = 100 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую на 1/3 его длины от конца стержня. (Ответ: J = 10-3 кг·м2.)
- Определите момент инерции сплошного однородного диска радиусом R = 40 см и массой m = 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. (Ответ: J = 0,12 кг·м2.)
- Физический маятник представляет собой стержень длиной l = 1м и массой m1 = 1кг с прикрепленным к одному из его концов диском массой m2 = 0,5 кг. Определите момент инерции такого маятника относительно оси, перпендикулярной плоскости в которой маятник совершает колебания и проходящей через точку, отстоящую на расстояние l/3 от конца стержня. (Ответ I = 0,09 кг·м2)
- Шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии согласно уравнению φ = A + Bt2 + Ct3 (А = 1рад, B = 2 рад/с2; С = -0,5 рад/с3). Определите момент сил для t = 3c. (Ответ: М = - 0,1 Н·м.)
- Вентилятор вращается с частотой n = 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав N = 50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Определите момент сил торможения и момент инерции вентилятора. (Ответ: 1) М = 0,1 Н·м; 2) I = 1, 59·10-2 кг·м2)
- Частота вращения маховика, момент инерции которого равен 120 кг·м2, составляет n = 240 об/мин. После прекращения действия на него вращающего момента маховик под действием силы трения в подшипниках остановился за время t = 3,14 мин. Считая трение в подшипниках постоянным, определите момент сил трения. (Ответ: М = 16 Н·м.)
- Определите массу однородного сплошного диска, насаженного на ось, к ободу которого приложена постоянная касательная сила F = 40 Н, если через t = 5c после начала действия силы его кинетическая энергия составляла 2,5 кДж. (Ответ: m = 16 кг)
- Платформа в виде диска радиусом R = 1,5 м и m1 = 180 кг вращается по инерции около вертикальной оси с частотой n = 10 мин-1. В центре платформы стоит человек массой m2 = 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы? (Ответ: v = 0,942 м/с)
- Человек, стоящий в центре вращающейся горизонтальной платформы, держит в руках стержень длиной l = 2,5 м и массой m = 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система (платформа и человек) обладает моментом инерции J = 10 кг·м2 и вращается с частотой v1 =12 мин-1. Определите частоту вращения v2 вращения системы, если стержень повернуть в горизонтальное положение. (Ответ v2 =8,5 мин-1)
- Вал в виде сплошного цилиндра массой m1 = 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2 = 2 кг. С каким ускорением будет опускаться гиря, если ее предоставить самой себе. (Ответ: а = 2,8 м/с2)
- На однородный сплошной цилиндрический вал радиусом R = 50 см намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с2. Определите момент инерции вала, массу М вала. (Ответ: J = 6,25,12 кг·м2; 2) М = 50 кг)
- Тело массой m1 = 0,25 кг, соединенное невесомой нитью посредством блока (в виде полого тонкостенного цилиндра) с телом массой m2 =0,2кг, скользит по поверхности горизонтального стола. Масса блока m =0,15 кг. Коэффициент трения тела о поверхность равен μ=0,2. Пренебрегая трением в подшипниках, определите: 1) ускорение а, с которым будут двигаться эти тела; 2) силы натяжения Т1 и Т2 нити по обе стороны блока. (Ответ: а =2.45 м/с2; 2) Т1 = 1,1 Н; Т2 = 1,47 Н).
- Колесо радиусом R = 30 см и массой m = 3 кг скатывается без трения по наклонной плоскости длиной l = 5м и углом наклона α = 25°. Определить момент инерции колеса, если его скорость в конце движения составляла 4,6 м/с.(Ответ: J = 0,259 кг·м2)
- С наклонной плоскости, составляющей угол α = 30° с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определите время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см. (Ответ: t = 0,585 с)






