СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
В методических указаниях приведено описание лабораторной работы, во время которой студенты знакомятся с формами представления сигналов, основами цифровой обработки сигналов и получения их спектров на основе аппарата Фурье. Спектральный анализ сигналов производится с использованием программного пакета MatLab
Методические указания предназначены для студентов
Содержание
1. Цель работы.............................................................................................. 4
2. Теоретическая часть.................................................................................. 4
2.1. Математическое описание сигналов...................................................... 4
2.2. Получение спектра сигнала................................................................... 6
2.3. Дискретное преобразование Фурье..................................................... 10
2.4. Быстрое преобразование Фурье.......................................................... 10
3. Описание лабораторной установки........................................................ 11
4. Порядок выполнения работы................................................................. 13
5. Требования к отчету................................................................................ 14
6. Контрольные вопросы............................................................................ 14
Список литературы..................................................................................... 14
Лабораторная работа
СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ
Цель работы
Целью данной работы является овладение навыками спектрального анализа сигналов.
Теоретическая часть
Математическое описание сигналов
Под сигналом понимают физический процесс, отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определенного типа.
Аналоговые сигналы (АС) описываются непрерывной (или кусочно-непрерывной) функцией x a (t), причем сама функция и аргумент t могут принимать любые значения на некоторых интервалах времени. Пример АС: x a (t)=Ae- a t , A= 1, a>0, вещественно, 0 ≤t, приведен на рис.2.1.а.

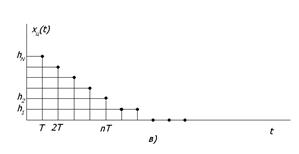
Рис. 2.1.
Аналоговые сигналы используются, например, в телефонии, радиовещании, телевидении.
Дискретные сигналы (ДС) описываются решетчатыми функциями – последовательностями – x(nT), где Т=const – интервал дискретизации, n – целое, n= 0, 1, 2, …; сама функция x(nT) может в дискретные моменты nT принимать произвольные значения на некотором интервале. Эти значения функции называются выборками, или отсчетами функции. На рис.2.1.б приведено графическое изображение ДС x(nT)=e a nT , a<0, вещественно, n= 0, 1, 2,…. Примером применения дискретных сигналов являются системы с амплитудно-импульсной модуляцией. Последовательность x(nT) может быть и конечной, состоящей из определенного конечного числа отсчетов: x( 0 )= 1, x(T)= -2, x( 2 T)= 3; конечную последовательность можно записать в форме x(nT)= {1, -2, 3}.
Цифровые сигналы (ЦС) представляют собой квантованные по уровню дискретные сигналы и описываются квантованными решетчатами функциями (квантованными последовательностями ) x ц (nT), принимающими в дискретные моменты nT лишь конечный ряд дискретных значений – уровней квантования h1, h 2 ,…, hN. Пример квантованного дискретного сигнала приведен на рис.2.1.в. Связь между решетчатой функцией x(nT) и квантованной решетчатой функцией x ц (nT) определяется нелинейной функцией квантования x ц (nT)=Fк (x(nT)). Существуют различные способы выбора функции квантования. В простейшем случае, когда используется квантование с постоянным шагом Dh=hi- hi- 1 =const, функция квантования имеет вид
 (2.1)
(2.1)
Каждый из уровней квантования кодируется числом, обычно используются двоичные символы 0, 1, и квантовые отсчеты x ц (nT) кодируются двоичными числами с m разрядами. Число уровней квантования N и наименьшее число разрядов m двоичных чисел, кодирующих эти уровни, связаны соотношением
 (2.2)
(2.2)
где int(A) – наименьшее целое число, не меньшее числа A.






