Примарные группы и их простейшие свойства
Определение 2.1.1. Группа  называется примарной, если её порядок равен степени некоторого простого числа.
называется примарной, если её порядок равен степени некоторого простого числа.
Теорема 2.1.1 (Свойства примарных групп). Пусть  – примарная группа.
– примарная группа.
1. Центр неединичной примарной группы отличен от 1.
Доказательство. Пусть  ‒
‒  -группа порядка
-группа порядка  и
и  ‒ все различные классы сопряженных элементов группы
‒ все различные классы сопряженных элементов группы  ,
,  Как известно, порядок класса сопряженных с
Как известно, порядок класса сопряженных с  элементов равен индексу централизатора
элементов равен индексу централизатора  , то есть
, то есть  . Каждый элемент центра составляет отдельный класс и наоборот, если
. Каждый элемент центра составляет отдельный класс и наоборот, если  то
то 
где  ‒ центр. Итак,
‒ центр. Итак,  где
где  при
при  Пусть
Пусть  Тогда
Тогда  Отсюда следует, что существует
Отсюда следует, что существует  такое, что
такое, что  Но тогда
Но тогда  и
и 
2. В примарной группе каждая собственная подгруппа отлична от своего нормализатора.
Доказательство. Пусть  ‒
‒  -группа и
-группа и  ‒ собственная подгруппа. Рассмотрим разложение группы
‒ собственная подгруппа. Рассмотрим разложение группы  в двойные смежные классы по
в двойные смежные классы по  :
:
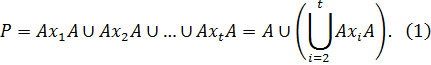
Здесь  Используя Теорему 1.2.2, получаем:
Используя Теорему 1.2.2, получаем:

Теперь из разложения  имеем
имеем
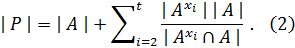
Пусть  Тогда из равенства
Тогда из равенства  следует, что
следует, что
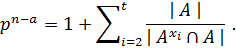
Так как  то в правой части равенства под знаком суммы имеются слагаемые, равные единице, то есть существует номер
то в правой части равенства под знаком суммы имеются слагаемые, равные единице, то есть существует номер  такой, что
такой, что  Это означает, что
Это означает, что  и
и  Ввиду того что
Ввиду того что  элемент
элемент  не принадлежит
не принадлежит  и
и  ‒ собственная подгруппа
‒ собственная подгруппа 
3. В примарной группе все максимальные подгруппы нормальны и имеют простые индексы.
Доказательство. Пусть  ‒
‒  -группа и
-группа и  По 2 пункту рассматриваемой леммы
По 2 пункту рассматриваемой леммы  ‒ собственная подгруппа в своем нормализаторе
‒ собственная подгруппа в своем нормализаторе 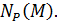 Из максимальности
Из максимальности  следует, что
следует, что  и
и  По теореме о соответствии в фактор-группе
По теореме о соответствии в фактор-группе  нет нетривиальных подгрупп, поэтому согласно теореме Силова группа
нет нетривиальных подгрупп, поэтому согласно теореме Силова группа  имеет простой порядок.
имеет простой порядок.
4. В примарной группе пересечение неединичной нормальной подгруппы с центром группы отлично от единицы.
Доказательство. Пусть  ‒
‒  -группа и
-группа и  Требуется доказать, что
Требуется доказать, что  Если
Если  ‒ произвольный элемент из
‒ произвольный элемент из  то
то  для любого элемента
для любого элемента  Поэтому
Поэтому  состоит из классов сопряженных элементов группы
состоит из классов сопряженных элементов группы  , то есть
, то есть  где
где  Можно положить
Можно положить  Поскольку
Поскольку  то, считая
то, считая 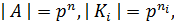 получаем
получаем

Теперь ясно, что существует  такое, что
такое, что  и
и 
5. Минимальная нормальная подгруппа примарной группы имеет простой порядок и содержится в центре группы.
Доказательство. Пусть  ‒
‒  -группа и
-группа и  Так как
Так как  то
то  , а поскольку
, а поскольку  то
то  Согласно теореме Силова в
Согласно теореме Силова в  существует элемент
существует элемент  простого порядка. Поэтому
простого порядка. Поэтому 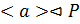 и из условия
и из условия  следует, что
следует, что  Теорема доказана.
Теорема доказана.
Определение 2.1.2. Пусть  Группа
Группа  называется
называется  -группой, если
-группой, если 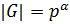 , где
, где 
Лемма 2.1.1 Пусть  Если
Если  – абелева группа и
– абелева группа и  , такая что
, такая что 
Теоремы Силова
Определение 2.2.1.
1) Пусть  где
где  Подгруппа
Подгруппа  группы
группы  называется силовской
называется силовской  -подгруппой группы
-подгруппой группы  (
( -силовской, силовой), если
-силовской, силовой), если  и обозначается
и обозначается  .
.
2) 
 множество всех силовских подгрупп группы
множество всех силовских подгрупп группы  (множество всех силовских
(множество всех силовских  -подгрупп группы
-подгрупп группы  ).
).
Теорема 2.2.1 (Первая теорема Силова). Пусть 
 Тогда в
Тогда в  существуют силовские
существуют силовские  -подгруппы.
-подгруппы.
Доказательство. Пусть  – контрпример минимального порядка.
– контрпример минимального порядка.
Расcмотрим 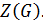
а) Пусть  .
.
По лемме 1.2.2(2)  . Так как
. Так как  .
.
Если 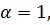 то
то  . Пусть
. Пусть  . Противоречие.
. Противоречие.
б) Пусть  не делится на
не делится на  . Рассмотрим формулу классов для
. Рассмотрим формулу классов для 
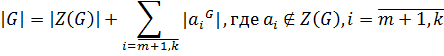
 не делится на
не делится на  Таким образом,
Таким образом,  Тогда по лемме 1.2.3(2)
Тогда по лемме 1.2.3(2)  не делится на
не делится на  . Следовательно, по теореме Лагранжа
. Следовательно, по теореме Лагранжа 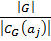 не делится на
не делится на  . Соответственно
. Соответственно 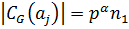 где
где 
Допустим, что 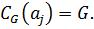 Тогда
Тогда 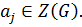 Противоречие. Следовательно,
Противоречие. Следовательно,  Тогда
Тогда  .
.
Таким образом,  Противоречие.
Противоречие.
Из а) и б) вытекает, что контрпримера не существует. Следовательно, утверждение верно для любой  . Теорема доказана.
. Теорема доказана.
Теорема 2.2.2 (Вторая теорема Силова).Всякая р -подгруппа группы  содержится в некоторой силовской
содержится в некоторой силовской  -подгруппе группы
-подгруппе группы 
Доказательство. Пусть  ‒ р -подгруппа группы
‒ р -подгруппа группы  . Тогда
. Тогда  ,
,  . Если β=0 ⇒
. Если β=0 ⇒  .
.
Если α=β ⇒ 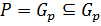 . Пусть
. Пусть  . Пусть
. Пусть  . Рассмотрим разложение
. Рассмотрим разложение  в двойные смежные классы по подгруппе
в двойные смежные классы по подгруппе  и
и 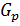 :
:

Следовательно,  Таким образом,
Таким образом, 
 такое что
такое что  не делится на
не делится на  Соответственно
Соответственно  , причем из
, причем из  . Теорема доказана.
. Теорема доказана.
Теорема 2.2.3 (Третья теорема Силова). Любые 2 силовские  -подгруппы группы
-подгруппы группы  сопряжены в
сопряжены в 
Доказательство. Пусть 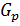 и
и  ‒ силовские
‒ силовские  -подгруппы группы
-подгруппы группы  . Покажем, что
. Покажем, что 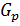 и
и  сопряжены в
сопряжены в  . Так как
. Так как  ‒
‒  -подгруппа группы
-подгруппа группы  , следовательно, по теореме 2.2.2
, следовательно, по теореме 2.2.2  для некоторого
для некоторого  и
и  сопряжены в
сопряжены в  . Теорема доказана.
. Теорема доказана.
Теорема 2.2.4 (Четвертая теорема Силова).Число силовских р -подгрупп группы  сравнимо с единицей по модулю
сравнимо с единицей по модулю  и делит
и делит 
Доказательство. Пусть  ‒ число силовских р -подгрупп группы
‒ число силовских р -подгрупп группы  . Пусть
. Пусть 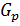 ‒ силовская р -подгруппа группы
‒ силовская р -подгруппа группы  . Тогда, по теореме 2.2.3, множество всех силовских р -подгрупп имеет вид:
. Тогда, по теореме 2.2.3, множество всех силовских р -подгрупп имеет вид:
 ⇒
⇒  .
.
Следовательно,  Из (1) ⇒
Из (1) ⇒ 
Рассмотрим разложение  в двойные смежные классы по подгруппе
в двойные смежные классы по подгруппе 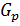 и
и 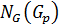 :
:
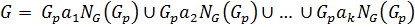 . Соответственно,
. Соответственно,  По формуле (2)
По формуле (2)  ⇒
⇒  Пусть
Пусть  . Тогда
. Тогда  Покажем, что
Покажем, что  . Допустим, что
. Допустим, что  не делится на
не делится на  . Тогда
. Тогда  , такое что
, такое что
 . Таким образом,
. Таким образом, 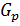 и
и  ‒ два разложения силовских р -подгрупп в
‒ два разложения силовских р -подгрупп в 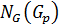 . С другой стороны,
. С другой стороны, 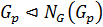 . Следовательно,
. Следовательно, 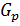 ‒ единственная силовская р -подгруппа в
‒ единственная силовская р -подгруппа в 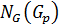 , что является противоречием. Таким образом,
, что является противоречием. Таким образом,  ⇒
⇒  ⇒
⇒  . Теорема доказана.
. Теорема доказана.






