1) Вычислить определитель:
a) 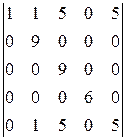 . (Областная, 1996, 15 мая)
. (Областная, 1996, 15 мая)
b) квадратной матрицы восьмого порядка, у которой на главной диагонали стоят числа 1 4 0 4 1 9 9 9, а вне ее тройки. (Областная, 1999, 14 апреля)
2) Числа 1081, 1403, 2093, 1541 делятся на 23. Докажите, что 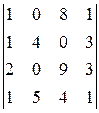 делится на 23. (Международная, 2002)
делится на 23. (Международная, 2002)
3) Не развертывая определителей, доказать следующие тождества
А) 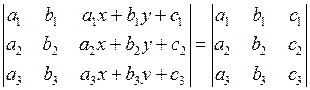 ;
;
Б) 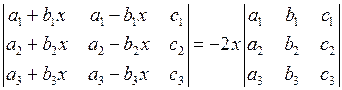 .
.
4) Вычислить определитель 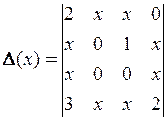 . (Международная, 2002)
. (Международная, 2002)
5) Пусть 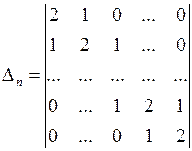 (по главной диагонали «двойки», над и под главной диагональю – «единицы», остальные – нули). Вычислить
(по главной диагонали «двойки», над и под главной диагональю – «единицы», остальные – нули). Вычислить 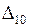 .
.
6) Вычислить 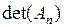 , если
, если 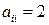 ,
, 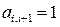 и
и 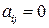 при
при 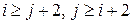 .
.
7) Вычислить 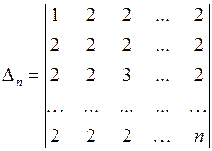 .
.
(Или 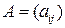 ,
, 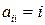 и
и 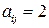 при
при 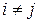 . Найти
. Найти  .)
.)
8) Вычислить 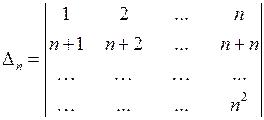 при
при 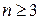 .
.
9) Вычислить 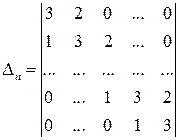 .
.
10) Для любого 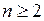 вычислить определитель
вычислить определитель  -го порядка
-го порядка
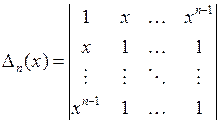 . (областная, 2011)
. (областная, 2011)
11) Решить уравнение 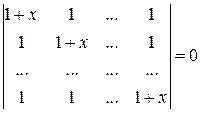 .
.
12) Вычислить 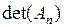 , если
, если 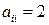 ,
, 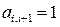 и
и 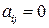 при
при 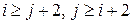 . (Международная, 2002)
. (Международная, 2002)
13) 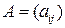 ,
, 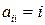 и
и 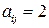 при
при 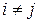 . Найти
. Найти  .
.
14) Доказать, что для матриц A и B, таких что 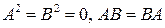
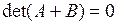 .
.
15) Как изменится определитель матрицы, если у всех его элементов изменить знак на противоположный? (П221)
16) Пусть 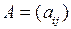 – антисимметрическая матрица 2007 порядка.
– антисимметрическая матрица 2007 порядка. 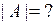
17) Пусть 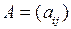 . Матрица B получена из матрицы A симметрией относительно побочной диагонали. Выразить
. Матрица B получена из матрицы A симметрией относительно побочной диагонали. Выразить  через
через 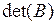 .
.
18) При каких 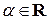 имеет решение матричное уравнение
имеет решение матричное уравнение 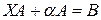 , где
, где 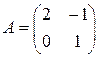 ,
, 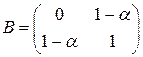 . Найти все эти решения.
. Найти все эти решения.
19) Доказать, что если в определителе порядка n на пересечении некоторых k строк и l столбцов, стоят элементы равные нулю, причем 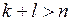 , то определитель равен нулю. (К 3.8.2)
, то определитель равен нулю. (К 3.8.2)
20) Как изменится определитель порядка n, если его матрицу повернуть на 90° вокруг «центра»? (П231)
21) Чему равен определитель, у которого сумма строк с четными номерами равна сумме строк с нечетными номерами? (П232)
22) Пусть A – квадратная матрица n -го порядка. Элементы 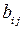 матрицы B выражаются через элементы
матрицы B выражаются через элементы 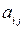 матрицы A по формуле
матрицы A по формуле 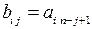 (
(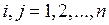 ). Матрица C получается из матрицы A заменой ее элементов на элементы, симметричные относительно побочной диагонали. Как связаны определители матриц В и A, С и А? (Областная, 1999)
). Матрица C получается из матрицы A заменой ее элементов на элементы, симметричные относительно побочной диагонали. Как связаны определители матриц В и A, С и А? (Областная, 1999)
23) Матрица Х является решением матричного уравнения 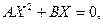 где
где 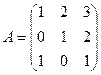 ,
, 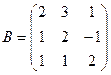 . Доказать, что
. Доказать, что  .
.
24) Пусть 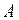 – квадратная матрица 2011-го порядка,
– квадратная матрица 2011-го порядка, 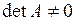 . Сколько решений имеет уравнение
. Сколько решений имеет уравнение 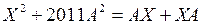 ? (Областная, 2011)
? (Областная, 2011)
25) Найти наибольшее значение определителя третьего порядка, составленного а) из чисел 0 и 1; б) из чисел 1 и –1. (К 3.8.1)
26) Решить уравнение 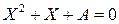 , если
, если 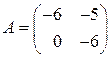 .
.
27) Среди всех определителей третьего порядка с элементами равными 1 или –1 найти наибольший.
28) Пусть 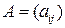 ,
, 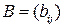 – симметрические матрицы (
– симметрические матрицы (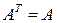 ,
, 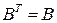 ) 2007 порядка. Доказать, что определитель
) 2007 порядка. Доказать, что определитель  равен нулю.
равен нулю.
29) Решить уравнение 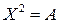 , если
, если 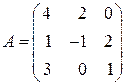 и X – целочисленна. (Указание: вычислить определитель от обеих частей)
и X – целочисленна. (Указание: вычислить определитель от обеих частей)
30) Найти все матрицы X второго порядка, удовлетворяющие равенству 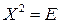 .
.
31) 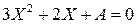 , если
, если 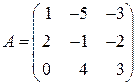 . Доказать, что нет решений. (Указание: выделить полный квадрат).
. Доказать, что нет решений. (Указание: выделить полный квадрат).
32) Найти все квадратные матрицы второго порядка, такие что 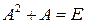 ,
, 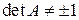 .
.
33) При каких n совместна система 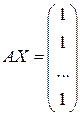 , A – антисимметрическая матрица.
, A – антисимметрическая матрица.
34) 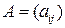 ,
, 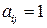 при
при 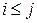 и
и 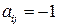 при
при 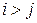 . Показать, что уравнение
. Показать, что уравнение 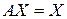 имеет ненулевое решение.
имеет ненулевое решение.
35) (М2, КЧ) Найти все числа c, умножение на которые невырожденной матрицы A не изменяет ее определителя. (П826)






