Изгиб с кручением круглого бруса.

Краткие сведения из теории

 

Брус находятся в условиях сложного сопротивления, если в поперечных сечениях одновременно не равны нуле несколько внут­ренних силовых факторов.

Наибольший практический интерес представляют следующие случаи сложного нагружения:

1. Косой изгиб.

2. Изгиб с растяжением или сжатием, когда в поперечном
сечении возникают продольная сила и изгибающие моменты, как,
например, при внецентренном сжатии бруса.

3. Изгиб с кручением, характеризующийся наличием в попе­
речных сечениях изгибающего (или двух изгибающих) и крутящего
моментов.

Косой изгиб.

 

Косой изгиб - это такой случай изгиба бруса, при котором плоскость действия суммарного изгибающего момента в сечении не совпадает ни с одной из главных осей инерции. Косой изгиб удобнее всего рассматривать как одновременный изгиб бруса в двух главных плоскостях zoy и zox, где ось z - ось бруса, а оси х и у - главные центральные оси поперечного сечения.

Рассмотрим консольную балку прямоугольного поперечного сечения, нагруженную силой Р (рис. 1).

Разложив силу Р по главным центральным осям поперечно­го сечения, получим:

Р_у=Рcos φ, Р_х=Рsin φ

В текущем сечении бруса возникают изгибающие моменты

М_х = - Р_уz = -Р_zcos φ,

М_у = Р_хz = Р_z sin φ.

рис.1

 

Знак изгибающего момента М_х определяется так же, как и в случае прямого изгиба. Момент М_у будем считать положи­тельным, если в точках с положительным значением координаты х этот момент вызывает растягивающие напряжения. Кстати, знак момента М_у легко установить по аналогии с определением знака изгибающего момента М_x, если мысленно повернуть сечение так, чтобы ось х совпала с первоначальным направлением оси у.

Напряжение в произвольной точке поперечного сечения бруса можно определить, используя формулы определения напряженна для случая плоского изгиба. На основании принципа независимости действия сил суммируем напряжения, вызываемые каждым из изгибающих моментов

(1)

В это выражение подставляются значения изгибающих моментов (со своими знаками) и координаты точки, в которой подсчитывается напряжение.

Для определения опасных точек сечения необходимо опреде­лить положение нулевой или нейтральной линии (геометрического места точек сечения, в которых напряжения σ =0). Максимальные напряжения возникают в точках, наиболее удаленных от нулевой линии.

Уравнение нулевой линии получаем из уравнения (1) при =0:

у = (2)

откуда следует, что нулевая линия проходит через центр тяжес­ти поперечного сечения.

Возникающими в сечениях балки касательными напряжениями (при Q_х≠0 и Q_у≠0), как правило, можно пренебречь. Если же возникает необходимость в их определении, то вычисляются вначале составляющие полного касательного напряжения τ_х и τ_у по формуле Д.Я.Журавского, а затем последние геометрически суммируются:

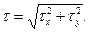(3)

 

Для оценки прочности бруса необходимо определить в опасном сечении максимальные нормальные напряжения. Так как в наиболее нагруженных точках напряженное состояние одноосное, то условие прочности при расчете по методу допускаемых напря­жений принимает вид

, (4)

 

где ,

- для пластичных материалов,

- для хрупких материалов,

n- коэффициент запаса прочности.

 

Если вести расчет по методу предельных состояний, то ус­ловие прочности имеет вид:

(5)

где R – расчетное сопротивление,

m – коэффициент условий работы.

В тех случаях, когда материал бруса различно сопротивля­ется растяжению и сжатию, необходимо определить как максималь­ное растягивающее , так и максимальное сжимающее напряжения, а заключение о прочности балки сделать из соотношений:

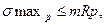
(6)

где R_p и R_c - соответственно расчетные сопротивления материа­ла при растяжении и сжатия.

Для определения прогибов балки удобно предварительно най­ти перемещения сечения в главных плоскостях по направлению осей х и у.

Вычисление этих перемещений ƒ_x и ƒ_y можно осуществить путем составления универсального уравнения изогнутой оси бал­ки или энергетическими методами.

Полный прогиб можно найти как геометрическую сумму:

ƒ= (7)

условие жесткости балки имеет вид:

ƒ_max , (8)

где - - допускаемый прогиб балки.

 

 

Внецентренное сжатие

 

В этом случае сжимающая брус сила Р направлена параллельно оси бруса и приложена в точке, не совпадающей с цент­ром тяжести сечения. Пусть Х_р и У_p - координаты точки прило­жения силы Р, отсчитанные относительно главных центральных осей (рис.2).

рис.2

Действующая нагрузка вызывает появление в попе речных сечениях следующих внутренних силовых факторов: N= -P, Mx= -Py_p, My=-Px_p

Знаки изгибающих моментов отрицательны, поскольку послед­ние вызывают сжатие в точках, принадлежащих первой четверти. Напряжение в произвольной точке сечения определяется выражением

(9)

Подставив значения N, Мх и Му, получим

(10)

Так как Ух= F, Уу= F (где i_x и i_y - главные радиусы инерции), то последнее выражение можно привести к виду

(11)

Уравнение нулевой линии получим, положив =0

1+ (12)

Отсекаемые нулевой линией на осях координат отрезке и , выразятся следующим образом:

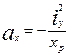, (13)

С помощью зависимостей (13) можно легко найти положе­ние нулевой линии в сечении (рис. 3), после чего определяются наиболее удаленные от этой линии точки, которые являются опасными, поскольку в них возникают максимальные напряжения.

Напряженное состояние в точках сечения - одноосное, по­этому условие прочности бруса аналогично ранее рассмотренному случаю косого изгиба бруса - формулы (5), (6).

При внецентренном сжатии брусьев, материал которых слабо сопротивляется растяжению, желательно не допустить появления в сечении растягивающих напряжений. В сечении возникнут напряжения одного знака, если нулевая линия будет проходить вне сечения или в крайнем случае касаться его.

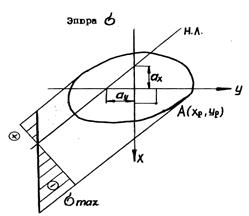
рис.3

Это условие выполняется тогда, когда сжимающая сила при­ложена внутри области, называемой ядром сечения. Ядро сечения - это область, охватывающая центр тяжести сечения и характер­ная тем, что всякая продольная сила, приложенная внутри этой зоны, вызывает во всех точках бруса напряжения одного знака.

Для построения ядра сечения необходимо задавать положение нулевой линии так, чтобы она касалась сечения, нигде не пере­секая его, и находить соответствующую точку приложения силы Р. Проведя семейство касательных к сечению, получим множество соответствующих им полюсов, геометрическое место которых даст очертание (контур) ядра сечения.

Пусть, например, дано сечение, показанное на рис. 4, с главными центральными осями х и у.

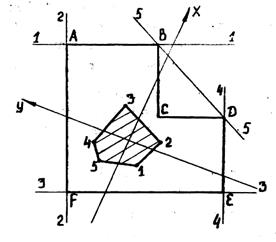
рис.4

Для построения ядра сечения приведем пять касательных, четыре из которых совпадает со сторонами АВ, ДЕ, EF и FA, а пятая соединяет точки В и Д. Измерив или вычислив от резки, отсекаемые указанными касательными I-I,...., 5-5 на осях х, у и подставляя эти значения в зависимости (13), определяем координаты х_р, у_р для пяти полюсов 1, 2....5, соответствующих пяти положениям нулевой линии. Касательную I-I можно перевести в положение 2-2 вращением вокруг точки А, при этом полюс I должен перемещаться по прямой и в результате поворота касательной перейти в точку 2. Следовательно, все полюсы, соответствующие промежуточным положениям касательное между I-I и 2-2, расположатся на прямой 1-2. Аналогично можно доказать, что остальные стороны ядра сечения также будут прямоугольными, т.е. ядро сечения - многоугольник, для построения которого достаточно соединить полюсы 1, 2,... 5 прямыми.

Изгиб с кручением круглого бруса.

При изгибе с кручением в поперечном сечении бруса в общем случае не равны нулю пять внутренних силовых факторов: М_х, М_у, М_к, Q_x и Q_у. Однако в большинстве случаев влиянием перерезывающих сил Q_x и Q_y можно пренебречь, если сечение не является тонкостенным.

Нормальные напряжения в поперечном сечении можно опреде­лять по величине результирующего изгибающего момента

Mu= . (14)

т.к. нейтральная ось перпендикулярна к полости действия момента М_u.

На рис. 5 изображены изгибающие моменты М_х и М_y в ви­де векторов (направления М_х и М_y выбраны положительными, т.е. такими, чтобы в точках первого квадранта сечения напряже­ния были растягивающими).

Направление векторов М_х и М_y выбрано таким образом, чтобы наблюдатель, глядя с конца вектора, видел их направлен­ными против движения часовой стрелки. В этом случае нейтраль­ная линия совпадает с направлением вектора результирующего мо­мента М_u, а наиболее нагруженные точки сечения А и В ле­жат в плоскости действия этого момента.

Наибольшие нормальные напряжения в этих точках равны

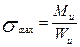, (15)

где Wu=Wx=

Максимальные касательные напряжения возникают в точках контура поперечного сечения и равны

 

рис.5

 

, (16)

где Wp=

Наиболее напряженными в сечении являются точки А и В, где напряжения и определяются соответственно по фор мулам (15) и (16).

рис.6

Напряженное состояние в этих точках, представленное на рис.6, является двухосным. Главные напряжения в этих точках равны

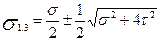, (17)

где и - напряжения, возникающие в точке на площадке, совпадающие с плоскостью поперечного сечения.

Условие прочности бруса при расчете по методу предель­ных состоим:

(18)

где R - расчетное сопротивление материала при растяжении,

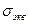- эквивалентное (расчетное) напряжение, определяемое на основании гипотез прочности,

m - коэффициент условии работы.

Если материал рассчитываемой детали относится к пластич­ным, то эквивалентное напряжение определяется либо по третьей теории прочности (теории наибольших касательных напряжений)

, (19)

либо по четвертой теории прочности (теории энергии формоизменения)

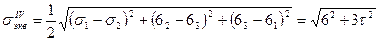. (20)

Если материал рассчитываемого бруса находится в хрупком состоянии, то эквивалентное напряжение вычисляется по пятой теории прочности Мора

, (21)

где К=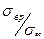

- предел прочности материала при растяжении;

- предел прочности материала при сжатии