Кафедра
«Информационные технологии в управлении»
Математика
Примеры решения и задания к контрольной работе №1
НАПРАСНИКОВА Ю. В., НАПРАСНИКОВ В. В.,
СОЛОВЬЕВ А. Н., СКАЛИУХ А. С.

М и н с к 2 0 0 9
Оглавление
Примеры решения задач. 5
Задания по вариантам.. 18
Литература. 31
Настоящий материал предназначен для использования в качестве методических указаний при выполнении контрольной работы студентами специальностей 25.01.07 «Экономика и управление на предприятии», 26.02.02 «Менеджмент», получающими образование на основе дистанционной формы обучения по дисциплине: «Математика».
Целью данной работы является приобретение студентами навыка решения задач, предусмотренных программой курса.
Составители:
преподаватель Ю.В. Напрасникова, канд. техн. наук, доцент В.В. Напрасников, (Белорусский Национальный технический университет, Республика Беларусь), д-р. физ.-мат. наук, проф. Соловьев А.Н. (Донской государственный технологический университет, Российская Федерация), канд. физ.-мат. наук, доцент Скалиух А.С. (Ростовский государственный университет, Российская Федерация)
Примеры решения задач
Задача 1. Вычислить пределы
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Решение:
а) При  имеем неопределённость вида
имеем неопределённость вида  . Для того, чтобы от неё избавиться, разложим числитель и знаменатель на множители. Будем иметь:
. Для того, чтобы от неё избавиться, разложим числитель и знаменатель на множители. Будем иметь:

б) При 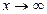 имеем неопределённость вида
имеем неопределённость вида  . Чтобы избавиться от неопределённости, разделим числитель и знаменатель дроби на старшую степень
. Чтобы избавиться от неопределённости, разделим числитель и знаменатель дроби на старшую степень  , входящую в дробь, т.е. на
, входящую в дробь, т.е. на  .Будем иметь:
.Будем иметь:

в) При  имеем неопределённость вида
имеем неопределённость вида  . Воспользуемся замечательным пределом
. Воспользуемся замечательным пределом  . Будем иметь:
. Будем иметь:
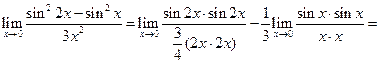
(сделаем замену в первом пределе 2x=y, 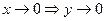 ) =
) =  .
.
г) Выделим целую часть дроби. Таким образом, получим неопределённость вида  при
при 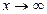 . Чтобы её раскрыть, воспользуемся замечательным пределом
. Чтобы её раскрыть, воспользуемся замечательным пределом  . Получим:
. Получим:

Ответ: а) 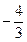 ; б)
; б)  ; в) 1; г)
; в) 1; г) 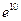 .
.
Задача 2. Найти угол между плоскостью 2x+3y-6z+1=0 и плоскостью, проходящей через точки  .
.
Решение:
Запишем уравнение плоскости  как уравнение плоскости, проходящей через три точки:
как уравнение плоскости, проходящей через три точки:


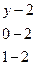
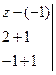 =0;
=0; 

 =0;
=0;



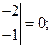
3(x-1)+6(y-2)+4(z+1)=0;
3x+6y+4z-11=0- уравнение плоскости  .
.
Угол между плоскостями  и
и  найдем по формуле
найдем по формуле
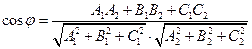 .
.
Будем иметь:
 Ответ:
Ответ:  /2.
/2.
Задача 3. Вычислить производные.
а)  б)
б)  в)
в) 
Решение:
а)

б) 
Прологарифмировав данную функцию, имеем:
 , т.е.
, т.е.  .
.
Продифференцируем обе части полученного равенства:
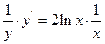 ,
,
отсюда 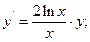

 .
.
в) Дифференцируя обе части равенства по x, считая у функцией от x, получаем:

Выразим 
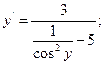
 .
.
Ответ: а)  ; б)
; б)  ;
;
в)  .
.
Задача 4. Найти производные первого и второго порядков от функции, заданной параметрически

Решение:
По определению первой производной для функции, заданной параметрически, получаем
 .
.
Окончательно первую производную запишем как функцию, заданную параметрически:

Тогда 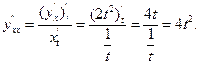
Следовательно, вторая производная имеет вид

Ответ: 

Задача 5. Раскрыть неопределённость по правилу Лопиталя.
а)  б)
б) 
Решение:
а) При 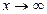 имеем неопределённость вида
имеем неопределённость вида 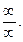 Будем применять правило Лопиталя последовательно 4 раза, то есть столько раз, чтобы получить в итоге число, а не неопределённость.
Будем применять правило Лопиталя последовательно 4 раза, то есть столько раз, чтобы получить в итоге число, а не неопределённость.
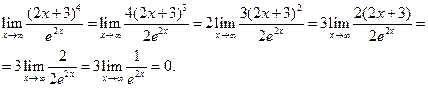
б) При  имеем неопределённость вида
имеем неопределённость вида  . После применения правила Лопиталя будем иметь:
. После применения правила Лопиталя будем иметь:

Ответ: а) 0;
б) 
Задача 6. Исследовать функцию и построить ее график

Решение:
1) Область определения 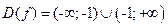 .
.
2) Функция непериодическая. Поскольку область определения не симметрична относительно нуля, то функция не является ни четной, ни нечетной.
3) Функция непрерывна в области определения как композиция основных элементарных функций. В точке  функция не определена. Исследуем поведение функции в окрестности этой точки
функция не определена. Исследуем поведение функции в окрестности этой точки

следовательно, точка  есть точка разрыва второго рода, а прямая
есть точка разрыва второго рода, а прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
4) Из пункта 3 имеем  - вертикальная асимптота.
- вертикальная асимптота.
Найдем наклонные асимптоты 

Получаем наклонную асимптоту  .
.
5) С помощью первой производной найдем точки возможного экстремума:


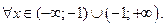

Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в таблице:
| х | (-∞;-4) | -4 | (-4;-1) | (-1;2) | (2;+∞) | |
знак 
| + | - | - | + | ||

|  возрастает возрастает
| -12 | 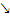 убывает убывает
| 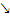 убывает убывает
|  возрастает возрастает
| |
| max | min |
Итак, функция убывает на интервалах (-4;-1) и (-1;2), и возрастает на интервалах (-∞;-4) и (2;+∞). В точке  имеет максимум
имеет максимум  , в точке
, в точке  имеет минимум
имеет минимум  .
.
С помощью второй производной найдем точки возможного перегиба:

Поскольку  для
для 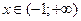 ,
,  для
для 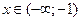 , то кривая, изображающая график функции, выпукла на интервале
, то кривая, изображающая график функции, выпукла на интервале  и вогнута на интервале
и вогнута на интервале  . Точек перегиба нет.
. Точек перегиба нет.
6) Построим график функции, используя результаты исследования

Задача 7. Исследуйте систему уравнений и в случае совместности решите ее
1) По формулам Крамера;
2) Матричным способом.
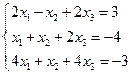
Решение:
1) Выпишем матрицу системы:
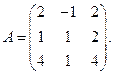
Найдем ее определитель:

следовательно, матрица А невырожденная, и система имеет единственное решение, которое может быть найдено по формулам Крамера.
Находим ∆i:
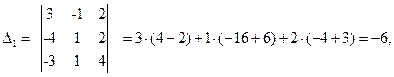


Тогда



2) Выпишем матрицу системы А и столбец свободных членов В:
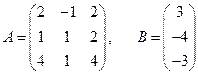 .
.
Тогда система примет вид:  , где
, где
 - столбец неизвестных.
- столбец неизвестных.
Умножим уравнение  на
на  слева:
слева:

Найдем  . Обратная матрица к
. Обратная матрица к  существует, так как матрица
существует, так как матрица  невырожденная
невырожденная 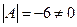 . Найдем алгебраические дополнения элементов матрицы
. Найдем алгебраические дополнения элементов матрицы  :
:
 Следовательно,
Следовательно,
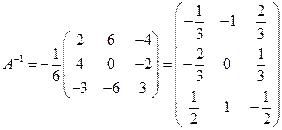 .
.
Произведение матриц  существует, т. к. число столбцов матрицы А равно числу строк матрицы В и равно 3. Найдем это произведение:
существует, т. к. число столбцов матрицы А равно числу строк матрицы В и равно 3. Найдем это произведение:

Ответ: 1; -3; -1.
Задача 8. Даны вершины треугольника А, В, С. Найти уравнение и длину высоты, опущенной из вершины В. Сделать чертеж.
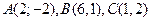
Решение:
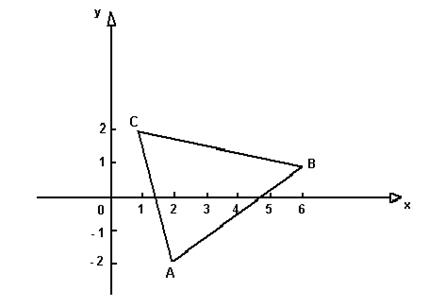
Сделаем чертеж треугольника.
Запишем уравнение высоты BD. Воспользуемся уравнением прямой, проходящей через заданную точку  перпендикулярно нормальному вектору прямой
перпендикулярно нормальному вектору прямой

Получим
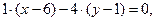
или
 - уравнение прямой BD.
- уравнение прямой BD.
Вычисляем длину высоты BD по формуле

которая позволяет вычислить расстояние от точки  до прямой
до прямой  (в нашем случае это прямая СА).
(в нашем случае это прямая СА).
Запишем уравнение прямой СА как уравнение прямой, проходящей через точку 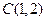 параллельно направляющему вектору
параллельно направляющему вектору 
Будем иметь

или
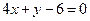 – уравнение прямой СА.
– уравнение прямой СА.
Тогда
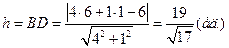
Ответ: 

Задания по вариантам
Схема выбора варианта:
| № зач. книжки | Номера Задач | № зач. книжки | Номера Задач |
| 1, 21 | 1, 21, 41, 61 и т.д. | 11, 31 | 11, 31, 51, 71 и т.д. |
| 2, 22 | 2, 22, 42, 62 и т.д. | 12, 32 | 12, 32, 52, 72 и т.д. |
| 3, 23 | 3, 23, 43, 63 и т.д. | 13, 33 | 13, 33, 53, 73 и т.д. |
| 4, 24 | 4, 24, 44, 64 и т.д. | 14, 34, 54, 74 и т.д. | |
| 5, 25 | 5, 25, 45, 65 и т.д. | 15, 35, 55, 75 и т.д. | |
| 6, 26 | 6, 26, 46, 66 и т.д. | 16, 36, 56, 76 и т.д. | |
| 7, 27 | 7, 27, 47, 67 и т.д. | 17, 37, 57, 77 и т.д. | |
| 8, 28 | 8, 28, 48, 68 и т.д. | 18, 38, 58, 78 и т.д. | |
| 9, 29 | 9, 29, 49, 69 и т.д. | 19, 39, 59, 79 и т.д. | |
| 10, 30 | 10, 30, 50, 70 и т.д. | 20, 40, 60, 80 и т.д. |
Найти пределы функций, не пользуясь правилом Лопиталя.
1. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 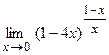 .
.
3. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
4. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 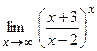 .
.
5. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
6. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 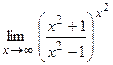 .
.
7. а)  ; б)
; б)  ;
;
в) 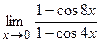 ; г)
; г)  .
.
8. а) 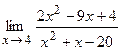 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
9. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
10. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 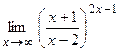 .
.
11. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
12. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 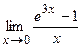 .
.
13. а) 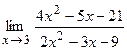 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
14. а)  ; б)
; б)  ;
;
в) 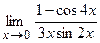 ; г)
; г)  .
.
15. а)  ; б)
; б) 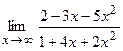 ;
;
в) 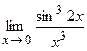 ; г)
; г)  .
.
16. а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 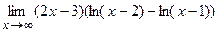 .
.
17. а)  ; б)
; б)  ;
;
в) 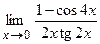 ; г)
; г) 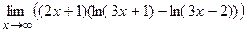 .
.
18. а) 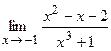 ; б)
; б) 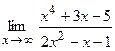 ;
;
в)  ; г)
; г) 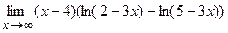 .
.
19. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 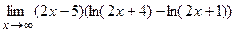 .
.
20. а)  ; б)
; б) 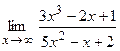 ;
;
в) 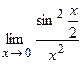 ; г)
; г)  .
.
2. (21-40). Найти угол между плоскостью 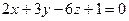 и плоскостью, проходящей через точки М1, М2, М3.
и плоскостью, проходящей через точки М1, М2, М3.
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
32. 
33. 
34. 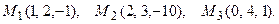
35. 
36. 
37. 
38. 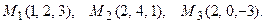
39. 
40. 






