Символический метод расчета цепей синусоидального тока

Сущность метода состоит в том, что для упрощения расчета цепей синусоидального тока переходят от уравнений для мгновенных значений, являвшихся по сути интегро-дифференциальными уравнениями, к алгебраическим уравнениям в комплексной форме. Расчет цепи удобнее вести для комплексных действующих величин синусоидальных токов и напряжений.

Для схемы (рис. 10) заданы следующие параметры:

 

 

r1 = 4,5 Ом, r2 = 5 Ом, r3 = 2,7 Ом, X1 = 3 Ом,

X2 = 1,5 Ом, X3 = 4,5 Ом, X4 = 3,5 Ом,

U = 14,76 В, Ψ_U = 54,37.

 

Рис. 7

Для заданной схемы определить токи в ветвях, записать баланс активных и реактивных мощностей, записать мгновенное значение тока и построить в масштабе топографическую диаграмму.

Порядок расчета:

А. Определяем комплексные сопротивления каждой ветви

,

,

.

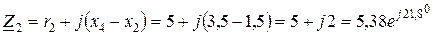Б. Определяем комплексное сопротивление разветвленного участка «ас»:

В. Определяем комплексное сопротивление всей цепи:

= ₁ + _ac = 4,5 + j3 + 3,29 – j1,13 = 7,79 + j1,87 = 7,95e^j13,57 ْ.

Г. Записываем приложенное напряжение в комплексной форме и определяем ток I₁в неразветвленной части цепи:

A.

Д. Определяем напряжение на разветвленном участке «ас»:

_ac= _{1 ac}= ×3,48e^-j19 ْ =6,46e^j21,8=(6+j2,4)В.

 

Е. Определяем токи в остальных ветвях:

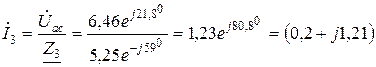A,

A.

Ж. Записываем мгновенное значение тока i₃ по его комплексному действующему значению =1,23ej^80,8ْ А.

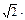
Комплексная амплитуда тока = = 1,23e^j80,8ْ,

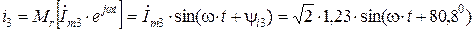А.

З. Комплексную мощность всей цепи определяем как =P±jQ,

где =14,76e^j54.37ْ В, İ ₁=1,85e^j40,8ْ А, =1,85e^-j40,8 ْ А, =14.76e^j54,37ْ ×1,85e^-j40,8ْ = =27,3e^j13,57ْ = (26,5+j6,4)ВА.

И. По закону сохранения энергии активная мощность всей цепи равна сумме активных мощностей всех n активных сопротивлений, входящих в цепь: =4,5×1,85²+5×1,2²+2,7×1,23²=26,52 Вт.

К. По закону сохранения энергии реактивная мощность всей цепи равна алгебраической сумме мощностей всех m реактивных сопротивлений, входящих в цепь (X_k>0, если сопротивление индуктивное и X_k<0, если емкостное): 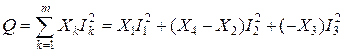=3×1,852+(3,5-1,5)×1,22+(-4,5)×1,232+

+6,43 Вт.

Баланс активных и реактивных мощностей сходится:

P=26,5≈26,52Вт Q=6,4≈6,43 Вт.

Л. Топографическая диаграмма — это векторная диаграмма цепи, в которой каждой точке электрической схемы соответствует точка на топо­графической диаграмме (рис. 8).

Это достигается тем, что векторы напряжений на отдельных элемента х схемы строятся в той последовательности, в которой они расположены в схеме (обходим схему в направлении тока).

Для построения топографической диаграммы определяем напряжения на всех элементах цепи.

 

U_r1 = I₁ R₁ = 1,85 × 4,5 = 8,34 В U_r3 = I₃ r₃ = 1,23 × 2,7 = 3,32 В

U_X1 = I₁ X₁ = 1,85 × 3 = 5,55 В U_X3 = I₃ X₃ = 1,23 × 4,5 =5,54 В

U_r2 = I₂ R₂ = 1,2 ×5 = 6 В I1 = 1,85 А

U_X2 = I₂ X₂ = 1,2 × 1,5 = 1,8 В I2 = 1,2 А

U_X4 = I₂ X₄ = 1,2 ×3,5 = 4,2 В I3 = 1,23 А.

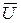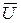М. Выбираем масштабы по току и напряжению μ_I = 0,25 А/см, μ_U = 1 В/см. Построение топографической диаграммы начинаем с разветвленного участка цепи, а именно ее второй ветви, содержащей большее число элементов. Из т. «а», отложив в произвольном направлении ток I₂, строим векторы _X2, _r2, 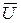_X4, ориентируя их соответствующим образом относительно тока I₂. Векторная сумма этих трех напряжений даст величину вектора 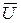_ас. Аналогичным образом строим напряжение 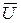_ас по току третьей ветви I₃. Совместим эти две диаграммы с помощью циркуля и линейки (по общему для них вектору 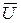_ас).

Отсюда определим положение векторов тока I₂ и I₃ относительно друг друга. Определяем ток в неразветвленной цепи по уравнению ₁= ₂+ ₃. Затем из т. «c», ориентируя вектора напряжени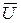й _X1 и 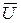_r1 относительно вектора тока ₁, строим вектор напряжения 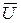_ab, равный в масштабе величине приложенного напряжения:

U = 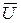ab×μu = 14,9 см×1В/см=14,9 В≈14,76 В.

Построенную топографическую диаграмму помещаем на комплексную плос­кость, отложив под углом –Ψ_u = -54,37° от вектора приложенного напряжения положительную ось вещественных чисел (при –Ψ_u<0 – угол откладываем по часовой стрелке, при -Ψ>0 - против). Если величины углов между векторами токов и положительной осью вещественных чисел равны соответственно аргументам комплексных действующих значений токов I₁, I₂, и I₃, то расчет цепи и построение топографической диаграммы верны.

 

 

Рис. 8

 

З А Д А Н И Е 1

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА

 

Задача 1

Расчет разветвленной цепи с одним источником электроэнергии.

По данным табл. 1, 2, 3 определить ток в неразветвленной части цепи и ветви, указанной в табл.1.

 

Рис. 9

 

Задача 2

По данным табл. 4 определить количество уравнений, необходимое и достаточное для определения токов во всех ветвях схемы по законам Кирхгофа. Составить эти уравнения в общем виде.

 

 

Рис. 10

 

Задача 3а

Пользуясь методом узлового напряжения, определить значения и направления всех токов в ветвях схемы по данным табл. 5, 6, 7. Составить численный баланс мощностей.

 

Рис. 11

 

Задача 3b

Пользуясь методом контур­ных токов, определить зна­чения и направления всех токов в ветвях схемы по данным табл. 5, 6, 7. Соста­вить численный баланс мощностей.

 

Рис. 12

 

Задача 3c

Пользуясь методом наложения, определить значения и направления всех токов в ветвях схемы по данным табл. 5, 6, 7. Составить численный баланс мощностей.

 

Рис. 13

 

Пример определения данных по варианту задания

 

Задача 1

 

табл. 1 табл. 2 табл 3

 

табл. 4 Задача 2

 

 

табл. 5 табл. 6 табл. 7

 

Задача 3

 

З А Д А Н И Е 2

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

Задача 1. Для электрической цепи, схема которой изображена на рис. 14 – 63 по заданным в табл. 8 сопротивлениям и Э.Д.С. выполнить следующее:

1) составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа;

2) найти все токи, пользуясь методом контурных токов;

3) проверить правильность решения, применив метод узлового напряжения; предварительно упростить схему, заменив треугольник сопротивлений R₄, R₅ и R₆ эквивалентной звездой, начертить расчетную схему с эквивалентной звездой и показать на ней токи;

4) определить ток в резисторе R₆ методом эквивалентного генератора;

5) определить показание вольтметра и составить баланс мощностей для заданной схемы;

6) построить в масштабе потенциальную диаграмму для внешнего контура.

 

 

 

Рис. 14 Рис. 15

 

 

 

 

Рис. 16 Рис. 17

 

 

 

 

Рис. 18 Рис. 19

 

 

 

 

 

 

Рис. 20 Рис. 21

 

 

 

 

Рис. 22 Рис. 23

 

 

 

 

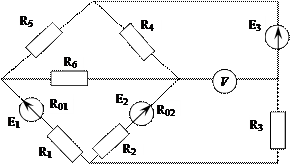Рис. 24 Рис. 25

 

 

 

 

 

Рис. 26 Рис. 27

 

 

 

 

 

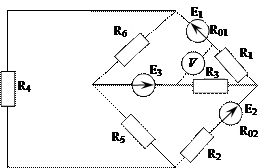
Рис. 28 Рис. 29

 

 

Рис. 30 Рис. 31

 

 

 

 

 

Рис. 32 Рис. 33

 

 

 

 

Рис. 34 Рис. 35

 

 

 

Рис. 36 Рис. 37

 

 

 

 

 

 

Рис. 38 Рис. 39

 

 

 

Рис. 40 Рис. 41

 

 

Рис. 42 Рис. 43

 

 

 

 

Рис.44 Рис. 45

 

 

 

 

 

Рис. 46 Рис. 47

 

 

 

Рис.48 Рис. 49

 

 

 

Рис. 50 Рис. 51

 

 

 

 

Рис. 52 Рис. 53

 

 

Рис. 54 Рис. 55

 

 

 

 

 

Рис. 56 Рис. 57

 

 

 

	E3

 

Рис. 58 Рис. 59

 

 

Рис. 60 Рис. 61

 

 

 

 

Рис. 62 Рис. 63

 

З А Д А Н И Е 3

СИМВОЛИЧЕСКИЙ МЕТОД РАСЧЕТА ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

 

По данным табл. 9, 10, 11рассчитать токи в ветвях заданной цепи при f = 50 Гц. Используя данные расчета, записать мгновенное значение указанной в табл. 9величины. Составить баланс мощностей. В масштабе построить топографическую диаграмму.

 

Пример определения данных по варианту задания:

 

табл. 9 табл. 10 табл. 11

 

 

 

 

 

Окончание табл. 1                                                                                                                                     -                                                                   Вариант Ветви, сопротивле- ния которых равны бесконечности (разрыв цепи) Ветви, сопротивле- ния которых равны нулю (К.З. ветви) Ветвь, в которой следует определить ток Вариант Ветви, сопротивле- ния которых равны бесконечности (разрыв цепи) Ветви, сопротивления которых равны нулю (К.З. ветви) Ветвь, в которой следует определить ток

Таблица 2         Окончание табл. 2                                                                                                 Вариант U,В Вариант U,В

Таблица 3     5,3       Окончание табл. 3           6,8                           6,3                                   4,8                     Вариант r, Ом Вариант r, Ом

Таблица 4             Окончание табл. 4                                                                                                 Вариант Цепь не содержит ветвей Вариант Цепь не содержит ветвей

Таблица 5     3a   Окончание табл. 5   3a       3c     3b     3c     3a     3b     3c     3a     3b     3c     3a     3b     3c     3a     3b     3c     3a     3b     3c     3a     3b     3c     3a     3b   Вариант № задачи Цепь не содержит ветвей Вариант № задачи Цепь не содержит ветвей

 

Таблица 6

 

Ва­ри­ант	E1, В	E2, В	E3, В	E4, В	E5, В	E6, В	E7, В	E8, В	E9, В	E10, В	U2, В

 

 

Таблица 7

Вариант	r1= r10, Ом	r1, Ом	r2, Ом	r3, Ом	r4, Ом	r5, Ом	r6, Ом	r7, Ом	r8, Ом	r9, Ом	r10, Ом

 

 

Таблица 8

Номер	Е1, В	Е2, В	Е3, В	R01, Ом	R02, Ом	R03, Ом	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
варианта	рисунка
	1,1				0,2	-	1,2
	1,2				0,8	-	0,8
	1,3				-	0,4	0,5
	1,4				-	0,6	0,8
	1,5				0,9	1,2	-
	1,1				0,1	-	1,1
	1,6				0,4	-	0,7
	1,7				0,8	0,3	-	3,5
	1,8				-	0,8	1,2
	1,9				-	0,2	0,6
	1,10				0,8	-	0,7	2,7
	1,11				0,9	-	0,5	9,0
	1,12				0,2	0,6	-	2,5
	1,13				0,8	1,4	-	4,2
	1,14				-	0,4	1,2	3,5
	1,15				1,2	0,6	-	2,0
	1,16				1,3	-	1,2	3,0
	1,17				0,7	1,5	-	6,0
	1,18				-	0,4	0,4	2,5
	1,19				0,5	-	0,5	3,5
	1,20				-	1,0	0,8	4,5
	1,21				1,0	-	1,2	5,0
	1,22				1,2	0,9	-	8,0
	1,23				-	0,8	0,8	3,0
	1,24				-	0,7	1,2	1,0
	1,25				1,0	0,4	-	1,0
	1,26				0,6	0,8	-	2,0
	1,27				0,6	-	1,0	1,5
	1,28				0,3	-	0,8	1,2

 

 

Окончание табл. 8

Номер	Е1, В	Е2, В	Е3, В	R01, Ом	R02, Ом	R03, Ом	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
варианта	рисунка
	1,29				-	0,2	0,2	3,0
	1,30				0,8	1,0	-	5,0
	1,31				0,2	-	1,2
	1,32				0,8	-	0,8
	1,33				-	0,4	0,5
	1,34				-	0,6	0,8
	1,35				0,9	1,2	-
	1,36				0,4	-	0,7
	1,37				0,8	0,3	-	3,5
	1,38				-	0,8	1,2
	1,39				-	0,2	0,6
	1,40				0,8	-	0,7	2,7
	1,41				0,9	-	0,5	9,0
	1,42				0,2	0,6	-	2,5
	1,43				0,8	1,4	-	4,2
	1,44				-	0,4	1,2	3,5
	1,45				1,2	0,6	-	2,0
	1,46				1,3	-	1,2	3,0
	1,47				0,7	1,5	-	6,0
	1,48				-	0,4	0,4	2,5
	1,49				0,5	-	0,5	3,5
	1,50				-	1,0	0,8	4,5

 

 

Таблица 9 Вариант Цепь не содержит элементов Определить мгн. значение указанной величины   r1 UL1   r2 UL2   r3 UL3   L1 i1   L2 i2   L3 i3   C1 UC2   C2 UC3   C3 UC1   L1, C2 UL2   L2, C1 UL1   L3, C2 UL2   L2, C3 UR1   L1, r2 UR3   L2, r3 i1   L3, r1 i2   C1, r1 i3   C2, r3 UR2   C3, r1 UL1   C1 i1   C2 i2   C3 i3   L1 UC1   L2 UL1   L3 UR1

Таблица 10 Вариант U, В Ψْu           -20           -50           -45 < ⇐ Предыдущая123 Поделиться с друзьями: Дата добавления: 2016-12-31; Мы поможем в написании ваших работ!; просмотров: 572 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: Ваше время ограничено, не тратьте его, живя чужой жизнью © Стив Джобс ==> читать все изречения... 1628 - | 1619 - © 2015-2024 lektsii.org - Контакты - Последнее добавление Ген: 0.142 с.