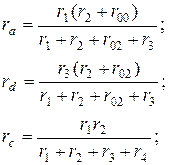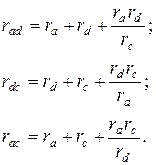Электрические цепи
Методические указания к самостоятельной работе студентов
по дисциплине «Электротехника и электроника»
Омск 2006
Составители: Е.М. Завьялов, В.Е. Завьялов, Р.Н. Хамитов
Печатается по решению редакционно-издательского совета
Омского государственного технического университета 
 |
Эквивалентные преобразования электрической цепи
Постоянного тока
Все задачи по расчёту простых электрических цепей постоянного тока можно свести к задачам двух типов. К первому типу относятся задачи, в которых даны параметры всех элементов цепи (сопротивлений и ЭДС) и требуется определить токи в некоторых или во всех сопротивлениях или напряжения на них. Ко второму типу относятся задачи, в которых известны параметры цепи – ток или напряжение, а требуется определить напряжение или токи в других участках или неизвестные параметры элементов цепи.
При решении этих задач применяются эквивалентные преобразования цепи, при которых токи и напряжения в непреобразованной части цепи остаются прежними. В результате этих преобразований упрощается исходная цепь и облегчается её расчёт.
Встречаются задачи, в которых положительное (действительное) направление искомого тока, напряжения, ЭДС не очевидно. В таких случаях выбирают произвольно для той или иной величины направление, которое в дальнейшем называют условно положительным. От выбора условно положительного направления искомой величины зависит только её знак. Если в результате расчёта окажется, что искомая величина имеет отрицательное значение, это означает, что действительное направление противоположно выбранному условно положительному.
Пример. На участке цепи, представленном на рис. 1, U12 = 10 В, E1 = 20 В,
E2 = 40 В, r1 = 5 Ом, r2 = 15 Ом.
Определить ток.
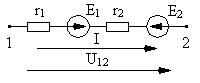Направление тока в этой задаче не очевидно. Зададимся условно положительным направлением тока, совпадающим с напряжением U12. Тогда, согласно закону Ома, для участка цепи с ЭДС:
Рис.1.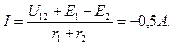 
Следовательно, направление тока в цепи встречно выбранному.
Преобразование пассивных ветвей
Пассивными являются ветви, не содержащие источников энергии.
А. Замена последовательных сопротивлений одним эквивалентным.
Сопротивления соединены последовательно, если они обтекаются одним током. Эквивалентное сопротивление цепи, состоящее из последовательно соединенных сопротивлений, равно сумме этих сопротивлений.
Например: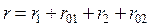 
.
Б. Замена параллельных сопротивлений одним эквивалентным.
Сопротивления параллельны, если все они присоединены к одной паре узлов. Эквивалентное сопротивление цепи, состоящей из параллельно соединённых сопротивлений, есть величина, обратная сумме проводимостей отдельных ветвей:
.
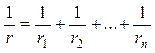В частном случае параллельного соединения двух и трёх сопротивлений эквивалентное сопротивление соответственно равно:
, 
.
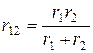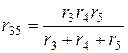В. Замена смешанного соединения сопротивлений одним эквивалентным.
Смешанное соединение – сочетание последовательного и параллельного соединений сопротивления.
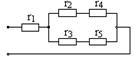
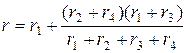
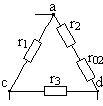
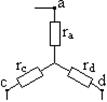
Г. Формулы преобразования треугольника сопротивлений в эквивалентную звезду и наоборот.
