Отчет по лабораторной работе №5
На тему
« Исследование одномерного прямолинейно-параллельного установившегося фильтрационного потока несжимаемой жидкости в неоднородных пластах»
По дисциплине: ____ Подземная гидромеханика_____________________
(наименование учебной дисциплины согласно учебному плану)
Выполнил: студент гр. НГ-09-2 _ / Чеботов А. Ю./
(подпись) (Ф.И.О.)
Проверил: преподаватель / Гладков П.Д./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
Цель работы:
Исследование прямолинейно-параллельного установившегося фильтрационного потока несжимаемой жидкости в неоднородных пластах.
Теоретические сведения:
|
а) б)
Рис. 1. Прямолинейно-параллельный поток в:
а) слоисто-неоднородном
б) зонально-неоднородном пластах
Рассмотрим особенности фильтрации в слоисто- и зонально-неоднородных волосообразных пластах:
а) случай слоисто-неоднородного пласта
Распределение давления в каждом из пропластков линейное и определяется выражением
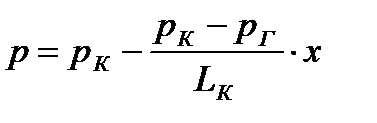(1)
где Рк - контурное давление, Па;
Рг - давление на галерее. Па;
Lк - длина пласта, м.
Градиенты давления в каждом пропластке постоянны и равны между собой:
(2)
Скорости фильтрации по пропласткам:
; (3)
(4) где μ - динамическая вязкость, Па 
с.
При равенстве градиентов давления в каждом пропластке из 2 следует справедливость следующего соотношения:
(5)
Т.е. для слоисто-неоднородного пласта скоростифильтрации по пропласткам прямо пропорциональны проницаемостям.
Дебит потока Q можно вычислить как сумму дебитов в отдельных пропластах Q1 и Q2:
(6)
, (7)
(8) где B- ширина пласта, м;
h1, h2– толщина пропластков.
(9)
Приравняв уравнение 8 и 9, получим средний коэффициент проницаемости:
(10)
б) случай зонально-неоднородного пласта
Распределение давления в каждом из пропластков линейное, но определяется следующими выражениями:
0 ≤ x ≤ l1 ; (11)
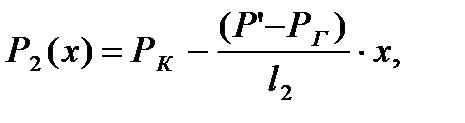0 ≤ x ≤ l2; (12)
где Р'- давления на границе 1 и 2 зон;
l1 и l2 - протяженности 1 и 2 зон, м.
Градиенты давления в каждой зоне постоянны, но не равны между собой, поскольку:
gradP1 
(13)
gradP2 
(14)
Скорости фильтрации по зонам соответственно:
(15)
(16)
Из уравнения неразрывности фильтрационного потока следует, что объемные расходы по зонам и по всей полосообразной залежи одинаковы, т.е. Q =v1F1= v2F2 означает, что v1=v2, т.к. F1=F2= 
.
Q1=v1F1=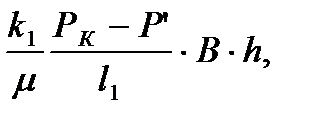 
(17)
Q2=v2F2 =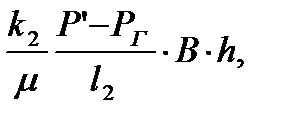 
(18)
Приравняем уравнения 15 и 16, 17 и 18 на основании следствия из уравнения неразрывности фильтрационного потока, получим соотношение
(19)
и 
,соответственно:
(20)
Коэффициент средней проницаемости вычисляется по формуле:
. (21)
Исходные данные:
Рк=9,7 МПа; Рг = 7,2 МПа; Lк =9 км; В = 120 м; μ =2 мПа*с; k1 = 0,7 мкм2; k2 = 0,4 мкм2; h1 = 4 м; h2 = 3 м; l1 = 4,5 км; l2 = 4,5 км.
Расчеты:
а) случай слоисто-неоднородного пласта
Закон распределения давления при установившейся фильтрации жидкости в слоисто- неоднородном пласте:
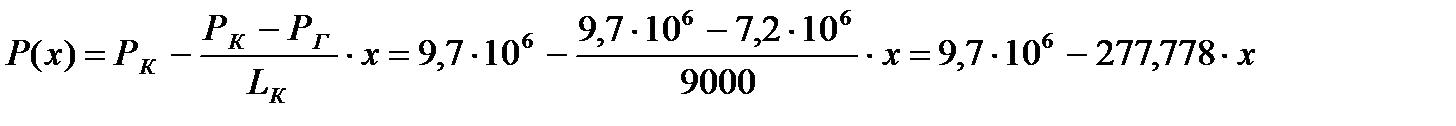Па.
Рис. 2. График распределения давления от координаты точки пласта, отсчитываемой от контура питания.
Градиенты давления в каждом пропластке постоянны и равны между собой:
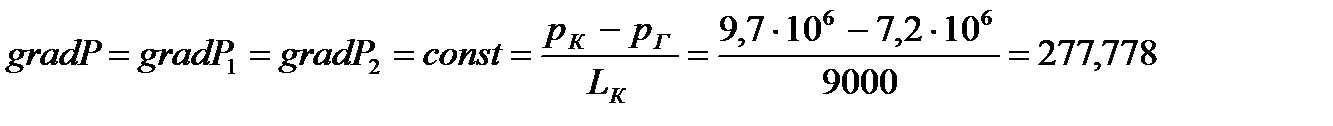Па/м.
Рис. 3. График распределения градиента давления по длине пласта.
Скорости фильтрации по пропласткам:
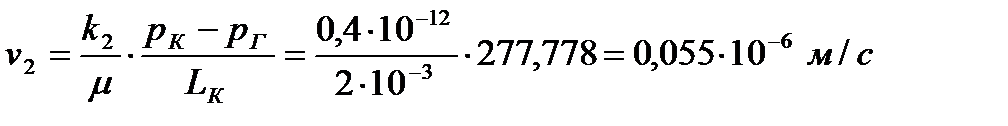
Рис. 4. График распределения скорости фильтрации по длине пласта
При равенстве градиентов давления в каждом пропластке следует справедливость следующего соотношения:
Дебит потока Q:
Средний коэффициент проницаемости залежи:
мкм2.
