Определение числа рейнольдса и режима движения воздуха

Отчет по лабораторной работе №5

 

 

 

Выполнил: студент гр. ГГ-09-2 ______________ / /

^{(подпись) (Ф.И.О.)}

 

 

Проверил:доцент ____________ /./

^{(подпись) (Ф.И.О.)}

 

Санкт-Петербург

2011 год

Цель работы - закрепить навыки работы с измерительными приборами и обработки результатов измерений, научиться определять режим движения воздуха в выработках.

 

Схема установки:

Общие сведения:

Движение воздуха по любому каналу может быть ламинарным или турбулентным. Режим движения воздуха в воздухопроводе определяется при помощи специального критерия – числа Рейнольдса

 

Re = v D / ν (24)

 

где: v – средняя скорость движения воздуха в воздуховоде, м/c; ν – кинематическая вязкость воздуха, ν = 1,5 10^-5 м²/с; D – гидравлический диаметр воздухопровода, м.

 

D = 4S / P (25)

 

где: S и P – соответственно площадь, м² и периметр, м поперечного сечения воздухопровода.

Экспериментально установлено, что в гладких трубах при Re ≥ 2300 устойчиво турбулентное движение, а при Re < 2300 устойчиво ламинарное движение. В горных выработках ламинарное движение воздуха переходит в турбулентное при Re = 1000 – 1500.

Закон движения воздуха в воздухопроводе описывается зависимостью

 

h = R Q ⁿ (26)

 

где: h – депрессия воздухопровода; R – аэродинамическое сопротивление трения в воздухопроводе; Q – количество воздуха, проходящего по воздухопроводу, м3 /c;

n – показатель степени, зависящий от режима движения воздуха: при ламинарном режиме n = 1, при турбулентном n = 2.

Таким образом, определив значение n в формуле (26), можно установить в каком режиме движется воздух.

Показатель степени n в формуле (26) определяется логарифмированием уравнения (26) и подстановкой в полученное выражение двух пар соответствующих значений h₁, Q₁, и h₂, Q₂ . Тогда при постоянном значении R

lg h₁ = lg R + n lg Q₁ ;

lg h₂ = lg R + n lg Q₂ .

Вычитая из первого уравнения второе, получим

lg h₁ - lg h₂ = n (lg Q₁ - lg Q₂ ),

откуда

 

n = (lg h₁ - lg h₂ ) / (lg Q₁ - lg Q₂ ) (27)

 

При выполнении лабораторной работы замеры величины депрессии h₁ и h₂ выполняются на участках 3–4 или 5–6. Каждый из этих участков прямолинеен, по всей длине имеет постоянную площадь поперечного сечения и закреплен одинаковой крепью. Поэтому единственным видом сопротивления движению воздуха на этих участках является аэродинамическое сопротивление трения R. Так как скорость движения воздуха по всей длине каждого из этих участков постоянна, то изменение скоростной депрессии здесь отсутствует. Поэтому депрессия, расходуемая на преодоление сопротивления участка, равна измеренной на этом участке статической депрессии, т.е. h _{ст 3-4} = h _{сопр 3-4} и h _{ст 5-6} = h _{сопр 5-6} (формулы (8) и (9)).

Одновременно с замером статической депрессии на исследуемом участке 3–4 или 5–6 выполняется замер статической депрессии на входе в установку h _{ст 0-1} для того, чтобы определить количество воздуха, поступающего в коллектор модели (см. работу 3). Если при этом шибер 2 полностью закрыт, то весь воздух, поступающий в коллектор, пойдет по верхней ветви и, следовательно, по участку 3–4, а если закрыт шибер 1 – по нижней ветви и участку 5–6.

При известном количестве воздуха средняя скорость его движения в любом сечении модели определяется по формуле

 

v _i = Q _i / S _i (28)

 

где: Q _i – расход воздуха в i-м сечении модели, м³ /с; S _i – площадь этого сечения, м² , принимается по табл.1.

 

 

Таблица измерений:

Ветвь модели	Участок, на котором Произво-дится замер	Вид измеряемой депрессии	Фактор при- бора, Км	Показа-тель спирта, Пс	Показания прибора	Депрессия h, мм вод. ст.	Перекрытие, %
Положение мениска в трубке прибора	Подъем уровня жидкости hн ,мм
Начальное h0 , мм	Конечное hк , мм
верхняя	0 – 1	Статическая	0,2	0,99524				18,9
3 – 4	0,4				4.4
2 – 3				22,3
0 – 1	0,2				16,1
3 – 4	0,4				3,6
2 – 3				18,3
0 – 1	0,2				6,4
3 – 4	0,4				0,8
2 – 3				6,8
0 – 1	0,2				3,8
3 – 4	0,4				0,4
2 – 3				3,6
нижняя	0 – 1	Статическая	0,2				17,7
5 – 6	0,4				21,5
1 – 5				41,0
0 – 1	0,2				12,9
5 – 6	0,4				15,1
1 – 5				32,2
0 – 1	0,2				7,6
5 – 6	0,4				8,0
1 – 5				16,3
0 – 1	0,2				4,0
5 – 6	0,4				3,6
1 – 5				8,0

Дополнительные данные:

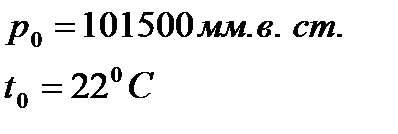
Примеры вычислений:

 

 

Исследуемая ветвь модели	Положение регулирующего шибера	Величина статической депрессии, мм. вод. ст.	Расход воздуха на участке Q m-n, м3 / с	Средняя скорость движения воздуха на участке V m-n, м / c	Число Рейнольдса Re	Показатель степени n
h ст 0-1	h ст m – n
Верхняя	Ш1 открыт	18,9	4,4	0,036	18,0	75428,6	3,1
Ш1 прикрыт	6,4	0,8	0,021	10,5	44000,0
Нижняя	Ш1 открыт	17,7	21,5	0,035	20,6	80438,1	2,4
Ш1 прикрыт	7,6	8,0	0,023	13,4	52323,8

Табл. №8

 

Примеры вычислений:

1. Вычисление гидравлического радиуса

2. Вычисление удельного веса воздуха

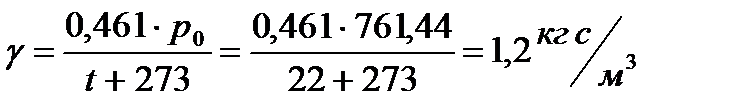
3. Вычисление скорости

4. Определение расхода воздуха на участке

5. Средняя скорость на участке

6. Определение числа Рейнольдса:

7. Определение показателя степени n

Выводы:

В ходе лабораторной работы было определено, что в моделе режим движения воздуха турбулентный. Также было найдено число Рейнольдса. Был определен показатель степени n, теоретическое значение которого при турбулентном режиме = 2. вычисленное значеное приблизительно равно теоретическому.