Введение
Цель работы - моделирование теплового режима электронного элемента радиоэлектронного средства (РЭА).
Порядок выполнения работы:
а) используя данные для своего варианта задания (согласно номера в списке группы) составить электротепловую модель системы печатная плата - окружающая среда.
б) используя программу расчета тепловых режимов конструкций РЭА “Асоника-П” в ее графическом редакторе построить тепловую модель, задавая конструктивные и теплофизические параметры ее тепловых ветвей.
в) запустив программу расчета “Асоника-П” определить температуры в узлах тепловой модели.
Тепловые режимы РЭА в значительной степени определяют надежность ее работы. Микроминиатюризация устройств электроники привела к необходимости еще больше обращать внимание на тепловые режимы аппаратуры.
Все элементы, из которых собрана аппаратура, должны работать в нормальном тепловом режиме. Тепловой режим отдельного элемента считается нормальным, если выполняются два условия: 1) температура элемента в условиях эксплуатации заключена в пределах, ограничивающих диапазон температур, допустимых для данного элемента; 2) температура элемента такова, что будет обеспечена его работа с заданной надежностью. Тепловой режим аппарата считается нормальным, если для всех элементов, смонтированных в аппарате, выполняются сформулированные выше условия.
Обеспечение нормального теплового режима является одной из главных задач, решаемых при проектировании аппаратуры. Для решения этой задачи принимается ряд мер: выбирают определенные типы элементов в зависимости от условий эксплуатации аппаратуры; вводят в аппаратуру специальные нагреватели, разогревающие ее при отрицательных температурах среды; применяют рациональное размещение элементов, узлов и блоков; выбирают форму и размеры отдельных конструктивных составляющих; применяют специальные средства охлаждения отдельных элементов и аппаратуры в целом. Как правило, меры, применяемые для обеспечения нормального теплового режима элементов и аппаратуры, приводят к увеличению габаритных размеров, необходимости установки дополнительного оборудования, перерасходу электроэнергии, увеличению веса и усложнению конструкции. Поэтому очень важно технически грамотно обосновать применяемые меры, то есть найти оптимальное решение, компромиссное между необходимостью обеспечить нормальный тепловой режим элементов и недопустимостью существенного увеличения потребления энергии, веса, габаритов и т. д. Обоснование применяемых мер может быть получено путем моделирования тепловых режимов проектируемой аппаратуры.
Топологическая модель тепловых процессов (МТП) представляет собой граф, вершины (узлы) которого моделируют соответствующие конструктивные элементы и узлы конструкции РЭА (они представляются в виде условно нагретых зон), а ветви (ребра) отражают тепловые потоки. Переменными узлов МТП являются расчетные значения температур, переменными ветвей будут тепловые потоки, а параметрами ветвей — тепловые проводимости. Данная модель позволяет в простой форме задавать различные граничные условия по объемам и поверхностям конструкции РЭА при помощи соответствующих компонентов графа (ветвей, источников заданной температуры и/или источников с заданной тепловой мощностью). К достоинствам топологических моделей следует отнести: возможность простого перехода, в случае необходимости, к другим унифицированным видам математических моделей РЭА; возможность применения единых методов формирования и решения математических моделей, включая аппарат теории чувствительности.
Исходные данные для моделирования на ЭВМ теплового режима РЭА подготавливаются на основе следующей информации:
· сборочного чертежа или деталировки конструкции РЭА (либо соответствующих эскизов);
· теплофизических параметров материалов, элементов конструкции РЭА и хладоносителей;
· значения тепловых мощностей, рассеиваемых элементами схемы РЭА;
· температуры окружающей среды;
· параметров охлаждения конструкции (температуры и скорости хладоносителей).
Необходимым условием правильного выполнения расчета является задание источника температуры и мощности, кроме того, необходимо наличие связей, определяющих теплопроводность.
Ветви, определяющие взаимодействие между элементами модели, имеют специальное обозначение: сплошная линия — кондукция, штриховая — конвекция, и т.д. Кроме того, имеются разновидности связей, которые обозначаются более сложно и задают комплексное воздействие, например, конвективно-кондуктивную связь оребренной поверхности радиатора.
При задании типовых элементов в диалоге с системой можно ввести все необходимые параметры для автоматического построения модели элемента. Кроме того, в любой момент можно изменить тот или иной параметр узла или ветви. При необходимости есть возможность взять данные из базы элементов и материалов, которые автоматически подключаются к модулям создания моделей.
После проведения расчета полученная информация отображается в двух вариантах. При стационарном тепловом расчете получается диаграмма температур в каждом узле модели и таблица температур и тепловых потоков, при нестационарном — таблица температур в зависимости от времени в каждом узле модели, а также графики зависимости функции T = y(t).
Основные теоретические положения теплообмена
Кондуктивный теплообмен

|
Тепловое сопротивление кондуктивной ветви
L
Rт = ¾¾¾,
l* F
где: L - длина пути теплового потока,
l - коэффициент теплопроводности материала,
F - площадь поперечного сечения теплового потока.
Рис. 2.1. Изображение кондуктивной ветви.
Конвективный теплообмен

|

|
Природа конвекции - перемешивание объемов с разной температурой, плотностью. Конвективный теплообмен происходит между твердым телом и газом или жидкостью. Конвективное сопротивление Rконв зависит от температурных напоров: чем больше разница, тем интенсивнее конвективный теплообмен; чем больше площадь поверхности, тем больше интенсивность теплообмена.
Рис. 2. 2. Модели конвективного теплообмена.
Рис.2.3. Коэффициенты для учета направления теплообмена.
На рисунке 2.2 показаны электротепловая (а) и тепловая (б) модели конвективного теплообмена. В электротепловой модели температура окружающей среды задается с помощью источника ЭДС. Конвективный теплообмен зависит от ориентации поверхности в пространстве. На рисунке 2.3 представлены коэффициенты, учитывающие ориентацию поверхности. Тепловое сопротивление конвективной ветви:
Rконв = ¾¾¾,
aк* S
где:
t1 - t2
aк = к A2(t1,t2) (¾¾¾)m,
L0
S - площадь поверхности,
aк - конвективный коэффициент теплообмена,
к - коэффициент ориентации поверхности в пространстве,
A2 - коэффициент, зависящий от температуры поверхности (t1) и температуры среды (t2),
L0 - определяющий (минимальный) размер поверхности в плане,
m – показатель степени (закон степени 1/8, 1/3 или 1/4).
Закон степени 1/8 - при охлаждении тонких, длинных стержней, режим - ламинарный, теплообмен незначительный.
Закон степени 1/4 - интенсивное ламинарное движение теплоносителя, теплообмен выше, чем в предыдущем случае.
Закон степени 1/3 - вихревое движение теплоносителя, теплообмен наиболее интенсивный из рассмотренных случаев.
Rконв рассчитывается в программе итерационным методом: задаемся Rконв, подставляем, рассчитываем тепловой режим (t1), уточняем значение Rконв и т. д. до необходимой точности.
Задание для моделирования
Произвести моделирование теплового режима прямоугольной текстолитовой платы с заданными (по вариантам) размерами, выделяемой тепловой мощностью и температурой окружающей среды. Ориентация платы – горизонтальная. Источник тепловой мощности находится в центре платы. В результате моделирования найти распределение температурного поля по плате (в узлах модели).
При построении модели используются типы элементов, приведенные на рис.3.1. Буква и цифры до тире обозначают тип элемента, а цифра после тире обозначает номер ветви тепловой модели.

Рис. 3.1. Элементы тепловой модели.
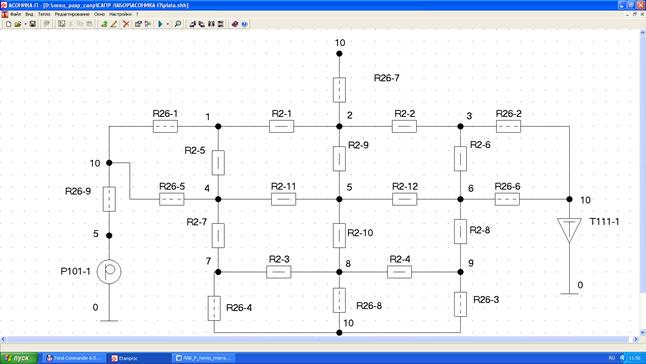
Рис. 2.8. Тепловая модель.
Назначение типов элементов тепловой модели, приведенных на рис. 2.7:
0-базовый (нулевой узел); 1- узел, моделирующий температуру электронного элемента или окружающей среды; R2-2 – кондуктивное тепловое сопротивление элемента платы; P101-1- источник тепловой мощности; T – источник постоянной температуры окружающей среды; R26-1 тепловое сопротивление конвективной ветви плата-окружающая среда.






