1. Ползун. Предположим, что тело (ползун) имеет вертикальную плоскость симметрии; пусть сечение этого тела этой плоскостью представляет собой прямоугольник со сторонами 
и 
.
|
|
|
|
Рис.12.5
К ползуну приложены вертикальная нагрузка 
и горизонтальная сила 
, линия действия которых будем считать пересекающимися в центре С прямоугольника. Реакция плоскости основания на ползун приводится к нормальной реакции 
и силы трения 
, причем линия действия неизвестна; ее расстояние от точки С обозначим через 
. Очевидно, что 
.
Составим уравнения равновесия плоской системы сил 
, .
, 
, 
.
Отсюда 
; 
; 
. →
Так как для равновесия 
, то 
.
Так как 
то 
.
Будем постепенно увеличивать 
. Если 
, то равновесие будет иметь место до тех пор, пока сила трения не достигнет предельной величины, после чего начнется скольжение ползуна, если же 
, то как только станет больше чем 
тело, раньше чем начнется скольжение, опрокинется вокруг ребра А.
2. Наклонная плоскость.
Рассмотрим ту же задачу, что и в предыдущем примере, но в предположении, что ползун положен на плоскость, наклоненную к горизонту под углом 
.
 |
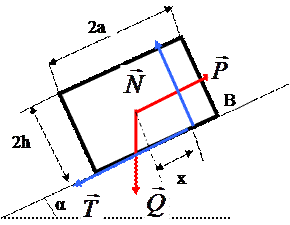Рис.12.6
Усилие, стремящееся сдвинуть тело вдоль наклонной плоскости, равно по величине
и направлено
а) вверх, если 
,
б) вниз, если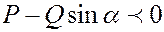 
.
В случае а) сила трения при покое направлена противоположно . Уравнения равновесия дают
; .
Для равновесия . То есть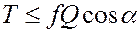 
или 
и 
.
Если постепенно увеличивать силу от значения 
, то при 
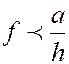равновесие будет иметь место до тех пор, пока не достигает значения, даваемого первым из этих неравенств; когда это значение будет превзойдено, тело начнет скользить вверх по плоскости. Если же 
и достигнет и превзойдет значение, даваемое вторым неравенством, то до наступления скольжения тело начнет опрокидываться вокруг правого ребра B.
В случае б) сила трения будет иметь направление силы . Как и выше, получим
, 
.
Рис.12.7
Если 
, то при постепенном уменьшении от значения равновесие будет иметь место, пока будет удовлетворено первое неравенство (в противном случае тело станет скользить вниз по наклонной плоскости). Наконец, при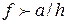 
равновесие имеет место если соблюдено второе неравенство (в противном случае произойдет опрокидывание вокруг левого ребра А).
В итоге можно сказать, что при равновесии сила P должна удовлетворять (при 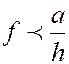) неравенствам
.
Если ввести в рассмотрение угол трения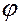 
, то это соотношение можно записать так:
.
Заметим, что при 
тело будет оставаться в равновесии при любом значении 
и при отсутствии силы (самоторможение на наклонной плоскости).
Равновесие тела при наличии трения качения
Рассмотрим цилиндр (каток), покоящийся на горизонтальной плоскости, когда на него действует горизонтальная активная сила 
; кроме нее, действуют сила тяжести , а также нормальная реакция и сила трения (рис.12.8(а)).
Как показывает опыт, при достаточно малой величины силы 
цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис.12.8(а). Согласно этой схеме, т.к. равновесие невозможно главный момент всех сил, действующих на цилиндр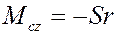 
, отличен от нуля и одно из условий равновесия не выполняется.
Причина выявившего-
ся несоответствия сос-
тоит в том, что в на-
ших рассуждениях
мы продолжаем поль-
зоваться представле-
Рис.12.8 (а) нием об абсолютно
твердом теле и предполагаем касание цилиндра с поверхностью, происходящим по образующей. Для устранения отмеченного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилиндр прижимается сильнее, чем в левой, и полная реакция 
приложена правее точки С (рис.12.8 (б)).
 |
|
Полученная теперь схема действующих сил статически удовлетворительна, т.к. момент пары (
) может уравновеситься моментом пары 
. Считая деформацию малой, заменим эту систему сил системой, изображенной на рис.12.8 (в). В отличие от первой схемы к цилиндру приложена пара сил с моментом 
.
Этот момент называется моментом трения качения. Составим уравнения равновесия цилиндра:
,
,
.
Первые два уравнения дают 
, 
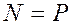, а из третьего уравнения можно найти 
.
Тогда 
. Как видно, с увеличением модуля активной силы растет расстояние 
. Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличиваться. Это значит, что наступает такое состояние, когда увеличение силы приведет к нарушению равновесия. Обозначим максимально возможную величину буквой 
(рис.12.8б). Экспериментально установлено, что величина пропорциональна радиусу цилиндра и различна для разных материалов.
=
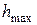Следовательно, если имеет место равновесие, то выполняется 
. (12.4)
Величина называется коэффициентом трения качения. Она имеет размерность длины.
Условие (12.4) можно также записать в виде 
. Учитывая, что 
, получим
.
Очевидно, что максимальный момент трения качения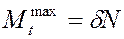 
пропорционален силе нормального давления.
В справочных таблицах приводится отношение коэффициента качения к радиусу цилиндра (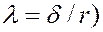
для различных материалов.
Задача. 
На наклонной плоскости находится цилиндр. Найти, при каких углах наклона плоскости к горизонту цилиндр будет находится в равновесии, если 
- радиус цилиндра, 
- коэффициент трения скольжения, - коэффициент трения качения.
Решение
Составим уравнения равновесия:
 |
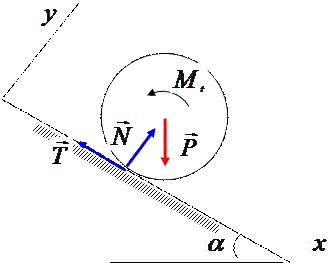Рис.12.9
,
,
.
Кроме того, должно выполняться:
;
Из первых трех уравнений мы можем определить 
, 
, . Подставим эти величины в последние два неравенства, получим
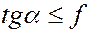; (12.5)
. (12.6)
Эти неравенства должны удовлетворяться одновременно. В тех случаях, когда 
, потеря равновесия происходит путем перехода к качению, так как сначала нарушится неравенство (12.6), если же 
, то нарушается неравенство (12.5) и цилиндр начнет скользить.
