Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо: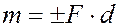 
Теорема Алгебраическая сумма моментов сил пары относительно любого центра, лежащего в плоскости ее действия, не зависит от выбора этого центра и равна моменту пары.
В самом деле. Возьмем в плоскости действия пары любую точку О. Найдем
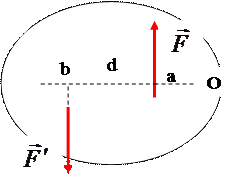
Рис.8.5
Сложим эти два выражения, получим
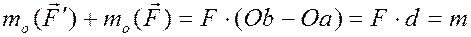
8.2.3. Эквивалентность пар
Не изменяя оказываемого на тело действия, можно пару сил, приложенную к абсолютно твердому телу, заменить любой другой парой, лежащей в той же плоскости и имеющей тот же момент.
док- во
Пусть на твердое тело действует пара сил (
с плечом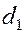 
. Проведем в плоскости действия пары через произвольные точки
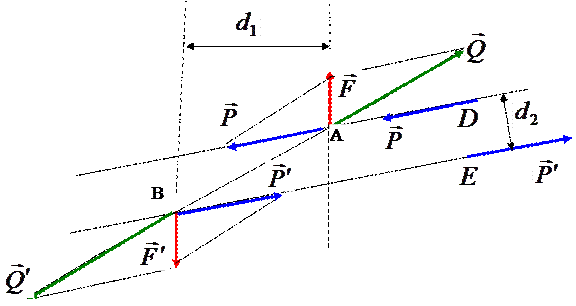
Рис.8.6
D и E две параллельные прямые до пересечения их с линиями действия сил пары (
) в точках А и В и приложим силы 
и 
в этих точках. Расстояние между прямыми AD и BE обозначим 
. Разложим теперь силу по направлениям ВА и DA на силы 
и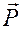 
, а силу - по направлениям АВ и BE на силы 
и 
. Очевидно, при этом 
, 
. Силы и , как уравновешенные, можно отбросить.
В результате пара сил 
будет заменена парой (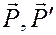
) с другим плечом и другими силами, которые можно, очевидно, приложить в точках D и E на их линиях действия. При этом, в силу произвола в выборе точек D и E, и направлений прямых AD и BE, пара 
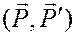может оказаться расположенной в плоскости ее действия, где угодно.
Покажем, что моменты пар (
и (
равны. В самом деле, так как сила является равнодействующей сил 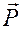и , то по теореме Вариньона
.
Но 
, 
, 
Следовательно, 
, т.е. моменты пар равны друг другу.
Из доказанной теоремы вытекают следующие свойства пары сил:
1) данную пару, не изменяя оказываемого ею на тело действия, можно переносить куда угодно в плоскости действия пары;
2) у данной пары, не изменяя оказываемого ею на тело действия, можно произвольно менять модули сил или длину плеча, сохраняя неизменным ее момент.
Отсюда следует, что две пары, лежащие в одной плоскости и имеющие одинаковые моменты, эквивалентны, т.к. указанными операциями (т.е. путем изменения плеча и перемещения в плоскости действия) они могут преобразованы одна в другую.
По доказанному следует, чтобы задать пару, лежащую в данной плоскости, достаточно задать ее момент; чему при этом равны силы пары или ее плечо и где пара расположена в плоскости действия - не существенно. Поэтому, особенно в технике, пару сил часто изображают круговой стрелкой, указывающей направление поворота, не изображая сами силы (рис.8.7)
Рис. 8.7
Сложение пар, лежащих в одной плоскости. Условие равновесия пар.
Теорема. Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.
док-во:
Пусть для определенности на тело действуют три пары с моментами 
, 
(рис.8.8). На основании теоремы об эквивалентности пар мы можем заменить эти пары тремя парами (
), (
),
(
имеющими общее плечо d и такие же моменты:
, - 
, 
|
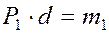Рис.8.8
Сложив теперь отдельно силы, приложенные в точках А и В, получим в точке В силу 
, а в точке А - силу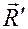 
, которые по модулю будут равны
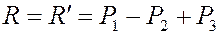
В результате вся система пар заменяется одной парой (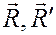
) с моментом 
Аналогично можно показать, что система, состоящая из n пар с моментами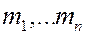 
заменяется одной парой с моментом 
.
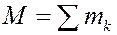Из этой теоремы вытекает, что для равновесие плоской системы пар
|
ПРИМЕР. На шестерню 1 радиуса 
действует пара сил с моментом 
. Определить момент пары, которую надо приложить к шестерне 2 радиуса 
чтобы сохранить равновесие.
Рис.8.9
Рассмотрим равновесие шестерни 1. На неё действует пара с моментом 
, которая может быть уравновешена только действием другой пары, в данном случае пары (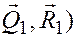
. Условие равновесия:
или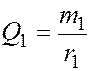 
.
Рассмотрим условия равновесия шестерни 2. На неё со стороны шестерни 1 действует сила 
, которая перпендикулярна к радиусу и образует с реакцией шарнира В пару 
с моментом 
. Эта пара и должна уравновеситься приложенной к шестерне 2 парой с моментом 
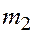. Условие равновесия 
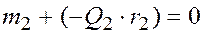. Так как 
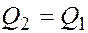, то получим 
.
