ЛЕКЦИЯ 2
8.1 С ложение и разложение параллельных сил
Найдем равнодействующую двух действующих на твердое тело параллельных сил. Возможны два случая:
1) силы направлены в одну сторону,
2) силы направлены в разные стороны.
Рассмотрим 1-й случай. На тело действуют две параллельные силы 
и 
(Рис.8.1).
Рис. 8.1
Приложим в точках А и В две уравновешенные силы 
и 
(
), направленные вдоль АВ, и сложим их с силами и по правилу параллелограмма.
Полученные силы 
и 
перенесем в точку О, где пересекаются их линии действия, и разложим на первоначальные составляющие. Силы и , как уравновешенные, можно отбросить. В точке О остаются две силы и , направленные вдоль одной прямой. Эти силы перенесем в точку С и заменим их равнодействующей 
, модуль которой равен 
.
Положение точки С определяется из соотношений
, (8.1)
которое получается из подобия соответствующих треугольников.
Итак: равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в ту же сторону; линия действия равнодействующей проходит между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных силам.
2- ой случай. Сложение двух сил, направленных в разные стороны
Рис.8.2
Пусть для определенности 
(рис.8.2). К точке С, лежащей на продолжении прямой BA, приложим уравновешенные силы и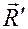 
, параллельные силам , . При этом модули сил и положение точки С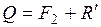 
выбираем так, чтобы удовлетворяли равенства
, (8.2)
Сложив силы и 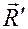, по формуле (8.1) найдем, что их равнодействующая 
будет по модулю равна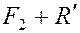 
, т.е. равна 
и приложена в точке А.
Силы и , как уравновешенные, можно отбросить. 
Окончательно, заданные силы и будут заменены одной силой , которая и является их равнодействующей. Модуль этой равнодействующей и ее точка приложения определяется формулами (8.2).
Таким образом: Равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в разные стороны, равна по модулю разности модулей слагаемых сил, им параллельна и направлена в сторону большей силы; линия действия равнодействующей проходит вне отрезка, соединяющего точки приложения слагаемых сил, на расстояниях от этих точек, обратно пропорциональных силам.
Заметим, что с помощью полученных формул можно решать задачу о разложении данной силы на две ей параллельных, направленных в одну или разные стороны.
8.2. Моменты и пары сил.
8.2.1 Момент силы относительно центра
Для оценки вращательного эффекта силы вводится понятие ее момента. Рассмотрим силу 
, приложенную в точке А твердого тела (Рис.8.3).
 | |||
 | |||
Рис.8.3
Перпендикуляр h, опущенный из центра О на линию действия силы, называется плечом силы относительно центра О.
Так как вектор силы можно перемещать вдоль линии ее действия, то вращательный эффект силы будет зависеть:
1) от модуля силы F и длины плеча h;
2) от положения плоскости поворота OAB, проходящей через центр О и силу ;
3) от направления поворота в этой плоскости.
Пусть все силы лежат в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается. Направление поворота можно охарактеризовать знаком, считая условно поворот в каком-нибудь одном направлении положительным, а в противоположном - отрицательным.
Для количественного измерения вращательного эффекта вводится следующее понятие о моменте силы:
Моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.
Обозначать момент силы относительно центра О будем символом 
. Следовательно: 
(8.3)
Если сила стремится повернуть тело вокруг центра О против хода часовой стрелки, то будем считать момент положительным, а если по ходу часовой стрелки -момент отрицательный.
Отметим следующие свойства момента силы:
1) момент силы не изменяется при переносе точки приложения силы вдоль линии действия;
2) момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю);
3) момент силы численно выражается удвоенной площадью 
.
8.2.2. Пара сил. Момент пары сил.
Парой сил называется система из двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рис. 8.4).
Рис.8.4
