ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
Лекция 1
Матрицы, определители. Системы линейных уравнений.
МАТРИЦЫ
Матрицей называется таблица чисел. Обозначается А или с указанием размерности 
, где 
– размерность: m – количество строк матрицы, а п – количество столбцов.
Элементы матрицы обозначаются 
, где i показывает номер строки, в которой находится элемент, а j – номер столбца.
Общий вид матрицы 
: 
.
Если количество строк матрицы совпадает с количеством столбцов и равно п, то матрица называется квадратной матрицей п-го порядка. Элементы квадратной матрицы, индексы которых одинаковы – 
, называются лежащими на главной диагонали или главной диагональю. Другая диагональ квадратной матрицы называется побочной.
ТРАНСПОНИРОВАНИЕ МАТРИЦ
Транспонированной по отношению к матрице А называется матрица 
, полученная из А записыванием элементов строк в столбцы и наоборот:
.
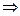
УМНОЖЕНИЕ МАТРИЦЫ НА ЧИСЛО И СЛОЖЕНИЕ МАТРИЦ
Чтобы умножить матрицу на число нужно каждый её элемент умножить на это число.
Сумма матриц одинаковой размерности есть матрица той же размерности, элементы которой равны суммам соответствующих элементов суммируемых матриц.
УМНОЖЕНИЕ МАТРИЦ
Действие выполнимо, если количество столбцов матрицы слева совпадает с количеством строк матрицы справа: 
, в результате получается матрица, у которой строк столько сколько у матрицы слева, а столбцов столько сколько у матрицы справа. Каждый элемент 
итоговой матрицы равен сумме произведений одноимённых элементов i -й строки матрицы слева и j -го столбца матрицы справа:
.
ОПРЕДЕЛИТЕЛИ МАТРИЦ
Определителем матрицы А второго порядка является число, равное разности произведений элементов главной и побочной диагоналей: 
, 
.
Определителем матрицы А третьего порядка называется число, найденное по формуле:
= 
Свойства определителей (на примерах определителей 2-го порядка):
Величина определителя:
1) не меняется, если матрицу A транспонировать, то есть строки заменить соответствующими столбцами:
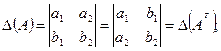
2) меняет знак, если у него переменить местами две строки (столбца):
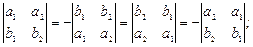
3) умножается на число k, если элементы строки (столбца) умножить на k:
то есть общий множитель в строке (столбце) можно выносить за знак определителя;
4) равна нулю, если элементы любого столбца (строки) равны нулю:
0× b 2-0× b 1= 0;
5) равна нулю, если имеются равные строки (столбцы):
a 1× a 2- a 2× a 2= 0;
6) не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k:
,
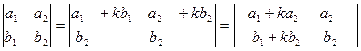(к I-й строке (столбцу) прибавить 2-ю строку (столбец), умноженную на число k
МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
Минором квадратной матрицы п -го порядка 
называется определитель матрицы п –1-го порядка, полученной вычёркиванием i -й строки и j -го столбца исходной матрицы.
Пусть дана матрица 
. Тогда 
, 
, 
.
Алгебраическим дополнением элемента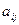 
квадратной матрицы называется число 
.
Для той же матрицы А: 
, 
, 
.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ РАЗЛОЖЕНИЕМ ПО ЛЮБОЙ СТРОКЕ И ЛЮБОМУ СТОЛБЦУ
Определитель квадратной матрицы п-го порядка есть число, равное сумме произведений элементов любой выбранной i -й строки или j-го столбца на их алгебраические дополнения.
.
Разложим определитель матрицы А по третьей строке:
Разложим определитель матрицы А по первой строке:
Разложить по 1 столбцу:
ОБРАТНЫЕ МАТРИЦЫ
Матрица 
называется обратной по отношению к квадратной матрице А если выполняется соотношение 
, где Е – единичная матрица – квадратная матрица на главной диагонали которой 1, а остальные элементы равны 0.
Обратные матрицы есть только у матриц, чей определитель не равен 0, в этом случае матрица называется невырожденной.
, где 
, а транспонированная матрица 
Найдём обратную матрицу по отношению к . 
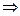
существует.
, 
, 
, 
, 
, 
, 
, 
, 
.
.
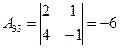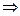
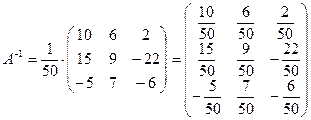Проверим по определению: 
.
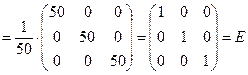Ранг матрицы.
Наибольший порядок отличных от нуля миноров матрицы А называется рангом матрицы А.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Общий вид системы линейных алгебраических уравнений из п уравнений с п неизвестными имеет вид: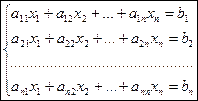 
, где 
– матрица системы, 
– вектор -столбец свободных членов системы, 
– вектор-столбец неизвестных.
Тогда систему уравнений можно записать в виде АХ=В
Решением системы является набор чисел х1=a1,х2=а2, …..хn=an, при подстановке которых в эту систему все уравнения превращаются в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение. Система, не имеющая ни одного решения, называется несовместной. Совместная система, имеющая единственное решение, называется определенной, если же система имеет более одного решения, она называется неопределенной. Решить систему-найти множество ее решений. Множество всех решений системы называется ее общим решением.
Определитель матрицы системы 
называется главным определителем системы. Определитель 
получается из главного заменой j- го столбцавектор-столбцом свободных членов системы В ( 
).
Для систем линейных алгебраических уравнений возможны следующие ситуации: система имеет единственное решение, система имеет бесконечное множество решений, система не имеет решений.
ПРАВИЛО КРАМЕРА
Если главный определитель системы 
, то система имеет единственное решение, которое находится по формулам: 
, 
,…, 
.
Решим систему методом Крамера.
, 
.
;
;
.
, 
, 
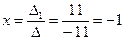. Проверка: 
Если главный определитель системы 
, то система либо имеет бесконечное множество решений, если 
; либо не имеет решений, если хотя бы один из определителей 
, .
МАТРИЧНЫЙ МЕТОД
Матричная форма записи системы линейных алгебраических уравнений имеет вид: 
. Если , у матрицы системы А существует обратная и справедливо равенство: 
. То есть, чтобы решить систему матричным методом нужно найти обратную матрицу к матрице А и умножить её на вектор-столбец свободных членов системы В.
Решим ту же систему матричным методом.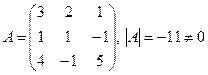 
.
, 
, 
, 
, 
, 
, 
, 
, 
.
.
.
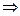
МЕТОД ЖОРДАНА-ГАУССА
| 
| … | 
| |
| 
| … | 
| 
|
| … | … | … | … | … |
| 
| … | 
| 
|
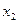
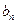
1. Записать систему в таблицу:
2. Среди коэффициентов при неизвестных, не равных нулю, выбрать ведущий элемент и обвести его в кружок. Строка, в которой он находится называется ведущей, а столбец – ведущим.
3. Новую таблицу получить по следующему алгоритму:
1) Ведущий элемент заменить единицей.
2) Остальные элементы ведущего столбца заменить нулями.
3) Остальные элементы ведущей строки разделить на ведущий элемент.
4) Оставшиеся элементы таблицы пересчитать по правилу прямоугольника: из элементов таблицы составляется прямоугольник так, чтобы пересчитываемый элемент с находился на диагонали с ведущим а. Тогда пересчитываемый элемент с изменяется по формуле: 
.
4. Для выполнения следующего шага в качестве ведущего элемента выбирается ненулевой коэффициент из тех строк и столбцов таблицы, которые не выступали в роли ведущих.
5. Преобразования Жордана-Гаусса проводятся до тех пор, пока есть возможность выбора ведущего элемента.
6. Из последней получившейся таблицы восстанавливается система уравнений в привычном виде, после чего делается вывод о наличии решений (нет противоречий) и выявляется само решение.
Пример
| x | y | z | |
 -1
| |||
| -1 | |||
| -5 |
|
|
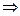
| x | y | z | |
  1
| -1 | ||
| -1 |
| x | y | z | |
| -1 | |||
| x | y | z | |
| -4 | -5 | ||
 3
| |||
| -11 | -22 |
