Лекция №8
Подземные объекты цилиндрической формы
Дифференциальные уравнения равновесия и движения среды при осесимметричных воздействиях
Рассмотрим элемент среды в цилиндрической системе координат (r,q, z), направив ось z вдоль оси симметрии. (Рис.8.1).
Рис.8.1. Элемент среды в цилиндрической системе координат
Объём элементарного элемента среды определяется выражением 
. Для осесимметричного поля деформаций справедливо предположение, что касательные напряжения, действующие на гранях элемента равны нулю, нормальные напряжения 
и 
не зависят от угловой координаты q. В таком случае можно записать единственное не тривиальное уравнение равновесия: 
(равенство нулю суммы проекций на ось r всех сил, действующих на элемент), которое после отбрасывания слагаемых высшего порядка малости и алгебраических преобразований можно представить в виде:
. (8.1)
Зависимость между напряжениями и деформациями определяется законом Гука. Для плоского деформированного состояния 
и закон Гука может быть представлен в форме:
, (8.2)
, (8.3)
где e – объёмная деформация
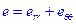, (8.4)
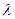и 
и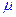 
характеристики упругой среды (параметры Лямэ).
Учитывая соотношения
, (8.5)
, (8.6)
представим уравнение равновесия (8.1) в перемещениях
. (8.7)
Следует отметить, что если граничные условия могут быть выражены в перемещениях, тогда решение не будет зависеть от упругих свойств материала, т.е. уравнение (8.7) можно записать в виде
. (8.8)
Добавляя в соответствие с принципом Даламбера в уравнение равновесия силы инерции элемента
, (8.9)
где 
плотность материала среды, получим
. (8.10)
Выражая напряжения через перемещения, получим уравнение движения
, (8.11)
где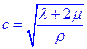 
скорость распространения продольных волн.
Уравнения (8.8) и (8.11) позволяют определять напряжёно деформированное состояние цилиндрических объектов, находящихся в упругой среде, так и самой среды при статическом и динамическом нагружении. Решение многих задач можно получить аналитически в замкнутом виде, используя метод разделения переменных, преобразование Фурье и другие интегральные преобразования. Во многих случаях интересно сравнить реакцию сооружения и среды на динамическое воздействие с реакцией при статическом нагружении. Поэтому в следующих параграфах рассматривается ряд решений, представляющих практический интерес в статической и динамической постановке.
8.2 Напряжённо деформированное состояние при статических воздействиях
Общее решение
Общее решение уравнения (8.8) можно представить в виде
, (8.12)
где A и B константы интегрирования, определяемые из граничных условий. Используя (8.5) и (8.6) можно получит интересное выражение для объёмной деформации
(8.13)
то есть объёмная деформация при таком виде деформированного состояния не зависит от координаты.
Напряжения определяются выражениями
, (8.14)
. (8.15)
Примеры
Сплошной цилиндр при действии равномерного внешнего давления
В центре цилиндра перемещения равны нулю. Граничные условия на внешней поверхности цилиндра определяются выражениями:
r = a: 
и (8.16)
отсюда следует:
(8.17)
В = 0 (8.18)
Напряжения внутри цилиндра
. (8.19)
Таким образом, поле напряжений однородное во всех точках цилиндра.
Поле деформаций определяется выражением
, (8.20)
т.е. перемещения линейно зависят от расстояния до центра цилиндра.
