Решение систем линейных уравнений методом Гаусса.

Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в по­следовательном исключении неизвестных.

Пусть дана система уравнений

,

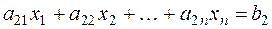, (3)

.

 

Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид

,

,

,

 

где k ≤ n, a_ii ≠ 0, . Коэффициенты a_ii называются главными элементами системы.

На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

Замечания: 1. Если ступенчатая система оказывается треугольной, т. е. k = n, то исходная система имеет единственное решение. Из последне­го уравнения находим х_n, из предпоследнего уравнения x_n-1, далее подни­маясь по системе вверх, найдем все остальные неизвестные (x_n-2,..., x₁).

2. На практике удобнее работать не с системой (3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строка­ми. Удобно, чтобы коэффициент а₁₁ был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a₁₁ ≠ 1).

Пример. Решить систему методом Гаусса:

,

,

.

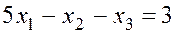Решение: Произведем элементарные преобразования над строчками расширенной матрицы системы:

~ ~ ~

 

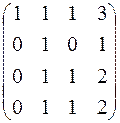Полученная матрица соответствует системе

x₁ + x₂ + x₃ = 3,

x₂ = 1,

x₃ = 1.

Осуществляя обратный ход, находим х_з = 1, х₂ = 1, х₁ = 1.

 

Системы линейных однородных уравнений.

Пусть дана система линейных однородных уравнений

,

,

.

 

Очевидно, что однородная система всегда совместна (r(А) = r()), она имеет нулевое (тривиальное) решение х₁ = х₂ =... = х_n = 0.

При каких условиях однородная система имеет и ненулевые решения?

Теорема 4. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа п неизвестных, т. е. r < п.

 

Теорема 5. Для того, чтобы однородная система п линейных уравнений с п не­известными имела ненулевые решения, необходимо и достаточно, чтобы ее опреде­литель Δ был равен нулю, т. е. Δ = 0.

 

Если система имеет ненулевые решения, то Δ = 0. Ибо при Δ ≠ 0 система имеет только единственное, нулевое решение. Если же Δ = 0, то ранг r основной матрицы системы меньше числа неизвестных, т. е. r < n. И, значит, система имеет бесконечное множество (ненулевых) решений.

 

Пример. Решить систему

x₁ – 2x₂ + 4x₃ = 0,

2x₁ – 3x₂ + 5x₃ = 0.

 

Решение: , r(A) = 2 (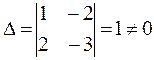), n = 3.

Так как r < n, то система имеет бесчисленное множество решений. Найдем

их.

x₁ – 2x₂ = – 4x₃,

2x₁ – 3x₂ = – 5x₃.

 

, . Стало быть,

, – общее решение.

Положив x₃ = 0, получаем одно частное решение: x₁ = 0, х₂ =0, x₃ = 0. Положив х₃ = 1, получаем второе частное решение: x₁ = 2, х₂ = 3, x₃ = 1 и т. д.