Дәріс мазмұны: сызықты ФЖС бар СИС сүзгілерінің типтері, олардың сипаттамалары, құрылымы мен қолданылуы.
Дәріс мақсаты: сызықтық ФЖС бар СИС сүзгілерінің төрт типін оқып үйрену, олардың құрылымы және Гильберт түрлендіргіші мен дифференциатор құру үшін сүзгінің белгілі-бір типін қолдану мүмкіндігі.
Рекурсивті емес сүзгілер практикалық тұрғыдан қарағанда үш маңызды қасиетке ие:
а) олар абсолютті тұрақты;
б) (2.7) айырымдылық функциясы немесе (2.8) беріліс фенкциясының 
коэффициенттері 
импульстік сипаттамасының санауы болып есептеледі
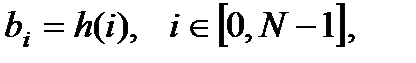
яғни т.е. импульстік сипаттамасының санауы мөлшері (
оның ұзындығы) мен оның соңғы ұзақтығы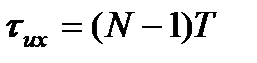 
;
в) тек СИС сүзгілері ғана сызықтық ФЖС қатаң түрде сақтай алады.
Соңғы сипаты импульстік сипаттама түрінен және келесі ережелермен анықталады:
СИС сүзгілері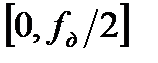 
жиілік диапазонында сызықты ФЖС болуы үшін жиіліктегі 
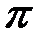радиан секірісінсіз, 
болған жағдайда оның импульстік сипаттамасының симметриалы болы қажет те жеткілікті
,
Немесе симметриялы емес
Бұл жағдайларда ФЖС еселенбеген нөлдері болғанда келесі формуламен есептеледі:
(4.1)
мұндағы 
– ИС ұзындығы;
- нормаланған жиілік;
– период частоты дискретизации;
– 
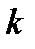жиілік нөмірі, және 
екендігі тек бөгелгеннен (басудан) кейін мүмкін, ал 
ИС симмертиялы болған жағдайында тек 0 мәнін қабылдайды және ИС симметриялы емес болғанда 1 мәнін қабылдайды;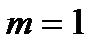 
теңдігі ФЖС 
радианында тұрақты жылжуды көрсетеді.
тақ немесе жұп және симметриялы немесе симметриялы емес болуына байланысты сызықты ФЖС бар СИС сүзгілерінің 2 кестеде келтірілгендей ИС төрт типі бар.
2 Кесте
ИС ұзындығы 
| Сүзгі реті
 =  -1
| Импульстік сипаттамасы | |
| симметриялы | симметриялы | ||
| Тақ | Жұп | 1ТипАЖС мінездемесі:
негізсіз; таңдалынатын кез-келген сүзгілер мен корректорлар синтезі, 
| 3 ТипАЖС мінездемесі:
Коэффициенттірден
тәуелсіз;
Гильберт
дифференциаторларының
түрлену синтезі,
|
| Жұп | Тақ | 2 ТипАЖС мінездемесі:
Коэффициенттерден тәуелсіз; ТЖ және жолақты сүзгілер синтезі,
| 4ТипАЖС мінездемесі:
 Коэффициенттірден тәуелсіз; Гильберт түрлендіргіші мен
дифференциаторлар
синтезі,
|
2 кесетеден көргеніміздей, СИС сүзгілерінің АЖС мен ФЖС әртүрлі ерекшеліктерге ие, бұл синтезделетін сүзгінің ерекшеліктерін алдын-ала білуге мүмкіндік береді.
СИС сүзгілерінің танымал түрлерінің бәрінен тәжірибеде көбінесе бұрылмалы сызықты кешігулері бар тура құрылымын қолданады, 4-Суретте көрсетілгендей аппаратты да, программалы да орындалуының жайы шарттастырылған. Бұндай құрылым үшін жадының 
ұяшықты көлемдегі буфер қажет, бірі мультиплексорлау режимінде жұмыс істейтін көбейткіш және екіншісі жинақтағыш сумматор. Дәл осы құрылымды сигналды процессордың ассебмлер тіліндегі программасы түрінде жүзеге асыруға болады, мысалы ТМS320С50.
| ) |
| ( |
| n |
| y |
| - |
| z |
| - |
| z |
| - |
| z |
| - |
| z |
| N-1 кешігу линиясы N11bvbf16h1111111NN.111111длиной N-1 |
| ) |
| ( |
| n |
| x |
| b |
| b |
| - |
| N |
| b |
| - |
| N |
| b |
| b |
| - |
| N |
| b |
4-Сурет
Сызықты ФЖС бар СИС сүзгілерінің коэффициенттер симметриясының коэффициенттер есебі 5-суретте көрсетілгендей қарастырылған құрылымды эквиваленттіге оңай түрлендіруге мүмкіндік береді.
5-Суретте Құрылымдар келтірілген (Nжұп және Nтақ үшін), олар тәжірибеде 2 есе аз көбейту (көбейткіш) талап етеді, сондықтан өш шуылы аз болады.
3 немесе 4 типті 
фазасының тұрақты жылжуы бар сызықты ФЖС бар СИС сүзгілері бірсызықты сигнал демодуляциясы негізінде 
төмен жиілікті, таржолақты сигнал айналымын алуға болатын сандық Гильберт түрлендіргішін (СГТ) құруға мүмкіндік береді, ол келесі формуламен анықталады:
(4.2)
мұндағы 
- жалған сигнал;
- заттық сигнал.
6 суретте 
иілетін 
сигналын есептеудің құрылымдық сұлбасы көрсетілген. Кідірудің келісілген сызығы (ККС) және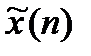 
сигналдардың уақыттық келісуін қамтамасыз етеді.
6 суретте көрсетілгендей, ККС мен ГЦТ фаза бойынша Из рисунка 6 видно, что СЛЗ и ЦПГ формируют пару сопряженных сигналов и 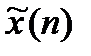, сдвинутых по фазе на 
.
На базе КИХ-фильтров типа 4 можно реализовать широкополосный дифференциатор, рабочая область которого составляет всю основную полосу нормированных частот, как показано на рисунке 7,а.
На рисунке 7,б показана реализация дифференциатора на базе КИХ-фильтров типа 3, АЧХ которыхдолжна обращаться в нуль на частоте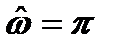 
.
Обычно цифровые дифференциаторы применяются в системах управления, где требуется линейное изменение коэффициента управления в зависимости от частоты воздействия.
