Вопросы: 1. Коммутативное кольцо с единицей. 2. Кольцо многочленов от одной переменной над коммутативным кольцом с единицей. 3. Степень многочлена. Свойства степеней многочленов. 4. Определение делимости многочленов нацело и с остатком. 5. Определение значения многочлена. Корень многочлена. 6. Теорема Безу. Схема Горнера. 7. Критерий корня. 8. Определение кратного корня многочлена. 9. Определение области целостности. 10. Определение и свойства производной многочленов. 11. Теорема о связи производной и кратности корня многочлена.
Пусть 
- коммутативное кольцо с единицей 1. Нуль этого кольца будем обозначать 0, элемент, противоположный к элементу 
, символом 
.
Кольцо многочленов от одной переменной с коэффициентами из кольца обозначается 
. Многочлен 
можно записать в стандартном виде: 
. Элементы из кольца являются многочленами, которые называют константами. Если 
, то многочлен имеет степень 
, которая обозначается 
. Степень константы, отличной от нуля, равна 0.
Степени многочленов обладают свойствами:
; 
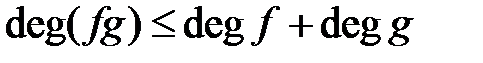
для любых многочленов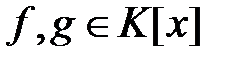 
.
Определение. Многочлен 
делится на многочлен 
в кольце , если найдется многочлен 
в этом кольце, что 
. Многочлен 
называется частным от деления.
Делимость многочлена на многочлен обозначается: 
.
Определение. Многочлен делится на многочлен 
в кольце с остатком, если найдутся многочлены 
и 
в этом кольце такие, что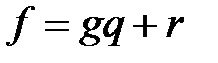 
, причем 
.
Разделить один многочлен на другой можно «уголком».
Пусть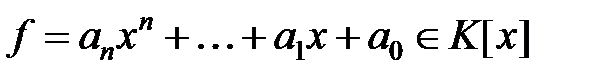 
, 
. Символом 
обозначается элемент кольца , который равен 
.
Определение. Элемент 
называется значением многочлена при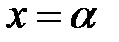 
.
Определение. Элемент 
называется корнем многочлена , если выполняется равенство: 
.
Следующая теорема названа в честь французского математика Этьенна Безу (1730-1783).
Теорема. Остаток от деления многочлена 
на многочлен 
, где 
, равен 
.
Деление многочлена 
на многочлен может быть осуществлено по схеме Горнера. (Метод назван в честь английского математика Уильяма Джорджа Горнера (1786-1837).) При этом находится частное от деления и остаток (значит, и значение функции ).
Схема Горнера: если
,
то
| 
| 
| … | 
| 
| |
| 
| 
| 
| … | 
| 
|
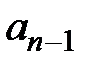
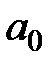
Из теоремы Безу получаем следующий критерий корня многочлена.
Теорема. Элемент является корнем многочлена тогда и только тогда, когда 
.
Определить, является ли элемент корнем многочлена можно, используя по схеме Горнера.
Определение. Корень 
многочлена называется корнем кратности 
, где 
, если 
и 
. Если 
, то корень называют простым корнем многочлена 
.
Определить кратность корня можно, используя схему Горнера.
Далее от кольца будет требовать большего, чем было заявлено раннее, а именно, 
- область целостности характеристики 0.
Определение. Коммутативное кольцо с единицей без делителей нуля называется областью целостностью.
Определение. Кольцо с единицей 1 называется кольцом характеристики 0, если для любого 
справедливо неравенство: 
.
Пусть 
.
Определение. Производной многочлена 
называется многочлен 
из кольца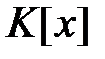 
такой, что 
.
Будем рассматривать кольца характеристики 0.
Очевидно, что 
.
-я производная многочлена определяется правилом: 
.
Верны равенства: 
; 
; 
; 
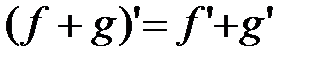для любых многочленов 
, 
и 
.
Теорема. Пусть 
- корень многочлена , кратности 
. Тогда - корень многочлена 
, кратности 
.
Используя эту теорему также можно определять кратность корня многочлена.
