Вопросы.1. Алгебраическое поле. 2. Кольцо многочленов от одной переменной над полем. 3. Степень многочлена. Свойства степеней многочленов. 4. Определение делимости многочленов нацело и с остатком. 5. Определение ассоциированных многочленов. 6. Определения приводимых и неприводимых многочленов. 7. Свойства неприводимых многочленов. 8. Определение нормированного многочлена. 9. Основная теорема о неприводимых многочленах.
Пусть 
- поле с единицей 1. Нуль этого поля будем обозначать 0, элементы, противоположный и обратный к элементу 
, соответственно символами 
и 
.
Кольцо многочленов от одной переменной с коэффициентами из поля 
обозначается 
. Многочлен 
можно записать в стандартном виде: 
. Элементы из кольца 
являются многочленами, которые называют константами. Если 
(старший коэффициент), то многочлен имеет степень 
, которая обозначается 
. Степень константы, отличной от нуля, равна 0.
Степени многочленов обладают свойствами:
; 
для любых многочленов 
.
Определение. Многочлен 
делится на многочлен 
в кольце 
, если найдется многочлен 
в этом кольце, что 
. Многочлен 
называется частным от деления.
Делимость многочлена на многочлен обозначается: 
.
Определение. Многочлен делится на многочлен 
в кольце 
с остатком, если найдутся многочлены 
и 
в этом кольце такие, что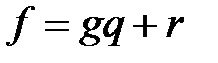 
, причем 
.
Разделить один многочлен на другой можно «уголком».
Определение. Многочлены 
называются ассоциированными, если выполняются условия: 
и 
.
Из определения следует, что если многочлены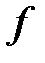 
и 
ассоциированы, то 
для некоторого ненулевого элемента 
.
Определение. Многочлен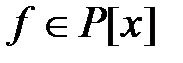 
, отличный от константы, называется неприводимым, если его делителями являются только константы и многочлены, ассоциированные с ним, в противном случае – приводимым.
Также используются следующее выражение: многочлен неприводим (приводим) над полем 
.
Свойства неприводимых многочленов над полем:
1) Если 
- многочлен первой степени, то он является неприводимым.
2) Если 
и 
- неприводимые многочлены и , то для некоторого ненулевого элемента .
3) Если 
- неприводимый многочлен и 
, то либо , любо многочлены и являются взаимно простыми.
4) Если - неприводимый многочлен и 
, то и многочлен 
является неприводимым.
5) Если - неприводимый многочлен, 
и 
, то хотя бы один из многочленов 
делится на многочлен .
Определение. Многочлен 
называется нормированным, если 
.
Следующая теорема называется основной теоремой о неприводимых многочленах.
Теорема. Любой многочлен, рассматриваемый над полем и отличный от константы, разлагается в произведение константы, отличной от нуля, и неприводимых нормированных многочленов, причем это разложение единственно с точностью до порядка следования множителей.
