Алгоритм кодирования методом Шеннона-Фано и Хаффмена.
Пример выполнения лабораторной работы:
Алгоритм метода Шенона - Фано:
1) Буквы алфавита сообщения записываются в таблицу в порядке убывания их вероятностей
2) Таблицу разделяют на две группы таким образом, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам из верхней группы таблицы ставится в соответствие в качестве первого символа символ 0, а всем буквам нижней – символ 1.
3) Каждая из полученных групп также разбивается на две подгруппы с приблизительно одинаковыми суммарными вероятностями. Всем буквам верхней подгруппы ставится в соответствие в качестве следующего символа символ 0, а всем символам нижней – символ 1.
4) Процесс повторяется до тех пор, пока в каждой подгруппе не останется по одной букве.
Теперь зашифруем такую поговорку:
У крошки Матрёшки пропали серёжки,
Нашёл на дорожке серёжки Серёжка.
У - 0010
Крошки - 10101 0000 10010 11001 10101 01010
Матрёшки - 111110 0110 1111110 0000 0100 11001 10101 01010
Пропали - 110000 0000 10010 110000 0110 111000 01010
Серёжки - 110001 10011 0000 0100 10001 10101 01010
Нашёл - 111001 0110 11001 0100 111000
На - 111001 0110
Дорожке - 1111011 1111110 0000 1111110 10001 10101 10011
Серёжки - 110001 10011 0000 0100 10001 10101 01010
Серёжка - 110001 10011 0000 0100 10001 10101 0110
Алгоритм метода Хаффмена:
1) Буквы алфавита сообщения записываются в таблицу в порядке убывания их вероятностей.
2) Две последние буквы (с наименьшими вероятностями) в этой таблице объединяются в одну вспомогательную, которой приписывается суммарная вероятность.
3) Все буквы, не участвовавшие в объединении с учетом вспомогательной упорядочиваются в порядке убывания вероятностей и записываются в дополнительный столбец. Две последние буквы снова объединяются во вспомогательную с суммарной вероятностью.
4) Процесс повторяется до тех пор, пока не будет получена одна единственная вспомогательная буква с вероятностью 1.
Зашифруем нашу поговорку:
У – 1110
Крошки – 11010 0000 01101 10101 11010 1001
Матрёшки – 0100011 00101 0011110 0000 10000 10101 11010 1001
Пропали – 101111 0000 01101 101111 00101 010110 1001
Серёжки – 10110 01100 0000 1000 01110 11010 1001
Нашел – 0101 00101 10101 1000 010110
На – 0101 00101
Дорожке – 0100010 01101 0000 01101 01110 11010 01100
Серёжки – 10110 01100 0000 1000 01110 11010 1001
Серёжка - 10110 01100 0000 1000 01110 11010 00101
Рассчитаем:
1.Энтропия источника сообщения есть величина, которая учитывает его вероятностные характеристики и вычисляется по формуле:
,
где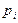 
- вероятность i-ой буквы алфавита сообщения;
n - число букв в алфавите сообщения.
Информацио́нная энтропи́я — мера неопределённости или непредсказуемости информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.
Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других.
Шеннон определил, что измерение энтропии, применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел.
2.Средняя длина кодовой комбинации является характеристикой эффективности оптимального кода и вычисляется по формуле:
,
где 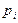- вероятность i-ой буквы алфавита сообщения;
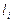- длина кодовой комбинации для і-ой буквы алфавита сообщения;
n - число букв в алфавите сообщения.
| Метод Шенона-Фано | Метод Хаффмена | ||||||
| pi | n | li | H | lср | li | lср | |
| р | 0,068966 | -0,26607 | 0,275864 | 0,275864 | |||
| ч | 0,068443 | ||||||
| у | 0,061621 | -0,24774 | 0,246484 | 0,246484 | |||
| й | 0,05479 | ||||||
| ё | 0,043103 | -0,19552 | 0,172412 | 0,172412 | |||
| и | 0,042103 | -0,19241 | 0,210515 | 0,168412 | |||
| я | 0,041878 | ||||||
| а | 0,041121 | -0,18932 | 0,164484 | 0,205605 | |||
| ъ | 0,039543 | ||||||
| щ | 0,036419 | ||||||
| в | 0,035143 | ||||||
| ж | 0,034483 | -0,16752 | 0,172415 | 0,172415 | |||
| о | 0,0344 | -0,16723 | 0,172 | 0,172 | |||
| е | 0,033276 | -0,16336 | 0,16638 | 0,16638 | |||
| ю | 0,031243 | ||||||
| к | 0,030345 | -0,15301 | 0,151725 | 0,151725 | |||
| г | 0,028429 | ||||||
| б | 0,027143 | ||||||
| п | 0,026841 | -0,14009 | 0,161046 | 0,161046 | |||
| с | 0,025862 | -0,13637 | 0,155172 | 0,155172 | |||
| ш | 0,025862 | -0,13637 | 0,12931 | 0,12931 | |||
| ц | 0,024729 | ||||||
| ь | 0,021529 | ||||||
| л | 0,021241 | -0,11804 | 0,127446 | 0,127446 | |||
| н | 0,017241 | -0,101 | 0,103446 | 0,068964 | |||
| х | 0,014929 | ||||||
| э | 0,014543 | ||||||
| ы | 0,011429 | ||||||
| з | 0,009343 | ||||||
| д | 0,008621 | -0,05912 | 0,060347 | 0,060347 | |||
| м | 0,008621 | -0,05912 | 0,051726 | 0,060347 | |||
| т | 0,008621 | -0,05912 | 0,060347 | 0,060347 | |||
| ф | 0,007143 | ||||||
| Итого: | 2,55142 | 2,581119 | 2,554276 |
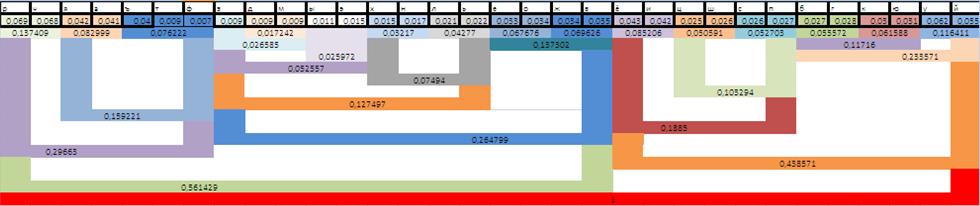
Вывод:
