Указания к выполнению индивидуальной работы №2

Костанайский филиал

Кафедра социально-гуманитарных и естественнонаучных дисциплин

 

 

УТВЕРЖДЕНО

заседанием кафедры СГЕНД

Протокол №__ от «___» _______ 2016 г.

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ

по изучению дисциплины

«Линейная алгебра»

Заочная форма обучения

 

 

Костанай, 2016 г.

Методические указания для студентов составлены:

Сизовой О.А., магистром математики, старшим преподавателем кафедры социально-гуманитарных и естественнонаучных дисциплин______________________________________

 

Методические указания для студентов обсуждены на заседании методической комиссии кафедры социально-гуманитарных и естественнонаучных дисциплин

Протокол №__ от «__» _________ 2016 г.

 

Председатель метод. комиссии __________________ И.А.Волошина

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ СРС

ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

СРС состоит из индивидуальных работ №1 и №2.

При оформлении и выполнении индивидуальной работы необходимо соблюдать следующие правила:

1. Задания выполняются в тонкой тетради в клеточку.
2. В начале работы (на обложке) должны быть ясно написаны фамилия студента и его инициалы, номер группы, предмет, вариант.
3. Индивидуальная работа выполняется синей пастой.
4. Решения задач необходимо сопровождать подробными пояснениями.
5. Индивидуальная работа, выполненная не по своему варианту, не зачитывается.

Указания к выполнению индивидуальной работы №1

Студенту необходимо выполнить индивидуальную работу №1 по варианту, номер которого определяется в соответствии с первой буквой фамилии студента. Индивидуальная работа состоит из двух заданий по темам «Матрицы и определители» и «Системы линейных алгебраических уравнений»

Примеры решения задач

Задача 1. Проверить совместность системы уравнений и в случае совместности решить ее: 1) по формуле Крамера; 2) с помощью обратной матрицы (матричным методом); 3) методом Гаусса.

Решение:

Проверяем совместность системы уравнений, для этого найдем ранг матрицы А и ранг расширенной матрицы В.

 

 

Найдем ранг матрицы А и ранг расширенной матрицы В.

В =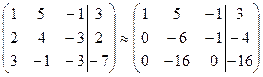

rang A = rang B = 3, значит система совместна

а) , ,

 

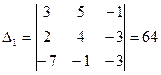, х₁= , х₂= , х₃= .

б) АХ= , Х=А^-1 ,

 

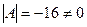
А₁₁= А₂₁= А₃₁=

 

А₁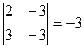₂=- А₂₂= А₃₂=

 

А₁₃= А₂₃=- А₃₃=

 

 

А^-1=

 

Задача 2. Для данного определителя найти миноры и алгебраический дополнения элементов . Вычислить определитель: 1) разложив его по элементам i-той строки; 2) разложив его по элементам j-го столбца.

Решение.

= = - 18 М₃₂= = - 20

 

А₁₂=(-1)¹⁺²М₁₂=-(-18)=18

 

А₃₂=(-1)³⁺²М₃₂=-(-20)=20

 

а) = а₁₁А₁₁+а₁₂А₁₂+а₁₃А₁₃+а₁₄А₁₄=

=-3 =-3*10-2*(-18)+1*32=38

 

б) 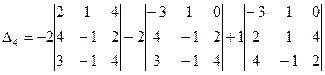=-2*(-18)-2(-4)+1*(-6)=38

 

в) Умножим третий столбец определителя на 3 и прибавим к первому, затем умножим на -2 и прибавим ко второму. Тогда в первой строке все элементы, кроме одного будут нулями.

 

=

 

=-(-56+18)=38

 

ИНДИВИДУАЛЬНАЯ РАБОТА №1

Первая буква фамилии	Вариант	Задание 1	Задание 2
		Для данного определителя найти миноры и алгебраический дополнения элементов . Вычислить определитель: 1) разложив его по элементам i -той строки; 2) разложив его по элементам j -го столбца.	Решить систему линейных алгебраических уравнений тремя способами: методом Гаусса, матричным методом и по правилу Крамера. Результаты сравнить.
А		i =4, j =1.
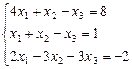
Б		i =3, j =3.
В		i =4, j =1
Г		i =1, j =3.
Д		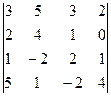i =2, j =4.
Е		i =1, j =2.
Ж		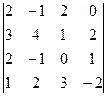i =2, j =3.
З		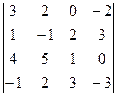i =3, j =1
И		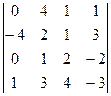i =4, j =3
К		i =4, j =2.
Л		i =4, j =1.
М		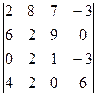i =3, j =3.
Н		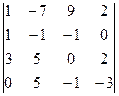i =4, j =1
О		i =1, j =3.
П		i =2, j =4.
Р		i =1, j =2.
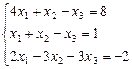
С		i =2, j =3.
Т		i =3, j =1.
У		i =4, j =3.
Ф		i =4, j =2.
Х		i =2, j =4.
Ц		i =1, j =2.
Ч		i =2, j =3.
Ш		i =3, j =1.
Щ		i =4, j =3.
Э		i =4, j =1.
Ю		i =3, j =3.
Я		i =4, j =1

 

Указания к выполнению индивидуальной работы №2

Студенту необходимо выполнить индивидуальную работу №2 по варианту, номер которого определяется в соответствии с первой буквой фамилии студента. Индивидуальная работа состоит из двух заданий по темам «Векторы на плоскости и в пространстве» и «Уравнение линии. Прямая и плоскость»

Примеры решения задач

Задача 1. Даны координаты вершин пирамиды

Методами векторной алгебры определить:

а) угол между ребрами А₁А₂ и А₁А₄,

б) площадь грани А₁А₂А₃

в) объем пирамиды

 

 

 

Решение:

а) угол между ребрами А₁А₂ и А₁А₄ найдем из скалярного произведения векторов и .

Для этого вычислим координаты и длины этих векторов, а также скалярное произведение векторов в координатной форме.

 

 

б) площадь грани А₁А₂А₃ найдем из геометрического смысла векторного произведения векторов и . Так как координаты вектора найдены в предыдущем пункте, то вычислим только координаты вектора и найдем координаты векторного произведения этих векторов.

 

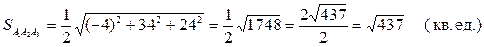
в) объем пирамиды найдем из геометрического смысла смешанного произведения векторов

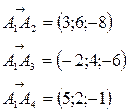
Координаты этих векторов были вычислены ранее. Смешанное произведение равно объему параллелограмма, построенного на приведенных к общему началу векторах.

Тогда, объем пирамиды вычислим по формуле

 

ИНДИВИДУАЛЬНАЯ РАБОТА №2

Первая буква фамилии	Вариант	Задание 1	Задание 2
Дана пирамида АВСD. Найти: а) объем пирамиды; б) площадь грани АВС; в) угол между ребром АВ и АС.	Даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) уравнение медианы АЕ; 4) уравнение и длину высоты СD; 5) уравнение прямой, проходящей через точку Е параллельно стороне АВ и определить координаты точки пересечения этой прямой с высотой СD. Сделать чертеж.
А		A(2,1,0); B(3,4,6); C(-2,1,5); D(1,4,5).	А (4; 0), В (7; 4), С (8; 2)
Б		A(1,5,-7); B(-3,6,3); C(-2,7,3); D(-4,8,-12).	А (2; 2), В (5; 6), С (6; 4)
В		A(-1,2,-3); B(4,-1,0); C(2,1,-2); D(3,4,5).	А (0; 2), В (3; 6), С (4; 4)
Г		A(1,2,0); B(3,0,-3); C(5,2,6); D(8,4,-9).	А (4; 1), В (7; 5), С (8; 3)
Д		A(0,-1,-1); B(-2,3,5); C(1,-5,-9); D(-1,-6,3).	А (3; 2), В (6; 6), С (7; 4)
Е		A(1,1,2); B(-1,1,3); C(2,-2,4); D(-1,0,-2).	А (-2; 1), В (1; 5), С (2; 3)
Ж		A(2,-4,-3); B(5,-6,0); C(-1,3,-3); D(-10,-8,7).	А (4; -3), В (7; 1), С (8; -1)
З		A(-1,2,4); B(-1,-2,-4); C(3,0,-1); D(7,-3,1).	А (-2; 2), В (1; 6), С (2; 4)
И		A(1,-5,-9); B(-1,-6,3); C(0,-1,-1); D(-2,3,5).	А (5; 0), В (8; 4), С (9; 2)
К		A(4,0,-1); B(2,3,8); C(-1,4,7); D(-3,4,-8).	А (2;3), В (5, 7), С (6; 5)
Л		A(5,8,-1); B(1,1,3); C(2,-3,2); D(7,1,9).	А(0,1); В(3,3); С(4,-1).
М		A(1,3,-3); B(-4,1,5); C(-2,1,6); D(-3,5,7).	А(-2,1); В(3,4); С(4,-3).
Н		A(1,4,2); B(1,-3,1); C(-1,1,0); D(-2,1,5).	А(0,3); В(4,0); С(-1,-2).
О		A(1,2,3);B(-2,3,-2);C(3,-4,-5); D(6,20,6).	А(5,1); В(2,-4); С(-1,3).
П		A(4,2,5); B(-3,5,6); C(2,-3,-2); D(9,4,18).	А(-1,-2); В(1,3); С(4,-1).
Р		A(1,2,4); B(1,-1,1); C(2,2,4); D(-1,-4,-2).	А(-2,3); В(4,1); С(5,-3).
С		A(3,2,2); B(2,3,1); C(1,1,3); D(5,1,11).	А(-3,1); В(1,6); С(2,-4).
Т		A(4,2,5); B(-3,5,6); C(2,-3,-2); D(9,4,18).	А(-1,-4); В(0,2); С(3,-1).
У		A(1,3,2); B(2,-5,7); C(1,3,-1); D(4,1,8).	А(3,4); В(-1,1); С(1,-2).
Ф		A(1,1,1); B(1,4,1); C(1,1,4); D(3,6,0).	А(2,-4); В(4,1); С(0,2).
Х		A(2,1,0); B(3,4,6); C(-2,1,5); D(1,4,5).	А(-2,-3); В(-1,4); С(1,2).
Ц		A(1,5,-7); B(-3,6,3); C(-2,7,3); D(-4,8,-12).	А(-1,-2); В(0,2); С(2,-2).
Ч		A(-1,2,-3); B(4,-1,0); C(2,1,-2); D(3,4,5).	А(1,-2); В(1,3); С(5,-2).
Ш		A(1,2,0); B(3,0,-3); C(5,2,6); D(8,4,-9).	А(0,5); В(7,0); С(-1,-2).
Щ		A(0,-1,-1); B(-2,3,5); C(1,-5,-9); D(-1,-6,3).	А(-1,2); В(1,3); С(3,-4).
Э		A(1,1,2); B(-1,1,3); C(2,-2,4); D(-1,0,-2).	А(0,3); В(1,-3); С(5,0).
Ю		A(2,-4,-3); B(5,-6,0); C(-1,3,-3); D(-10,-8,7).	А(-2,-4); В(-1,2); С(2,-1).
Я		A(-1,2,4); B(-1,-2,-4); C(3,0,-1); D(7,-3,1).	А(0,-1); В(2,2); С(-4,0).