Исходные данные к задаче - 6, 7, 8, 9

 

Вариант	Заданная нагрузка	Длины участков, м
F1, кН	F2, кН	q, кН/м	М, кНм	h	a	в	с
					2,0	1,6	1,2	0,5
					2,2	1,8	1,4	0,6
					2,4	2,0	1,6	0,7
					2,6	2,2	1,8	0,8
					2,8	2,4	2,0	0,9
					3,0	2,6	2,2	0,8
					3,2	2,8	2,0	0,7
					2,8	3,0	1,8	0,6
					2,6	2,8	1,6	0,5
					2,4	2,6	1,4	0,4

 

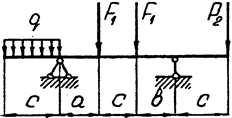
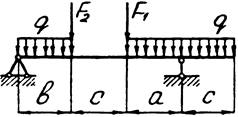
Задача 6. Двухопорная балка

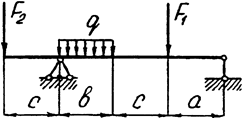
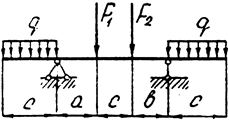
Задача 6 (продолжение)

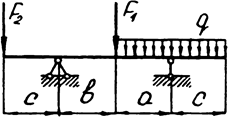
Задача 6 (окончание)

 

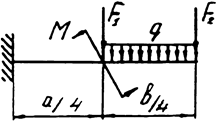
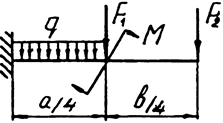
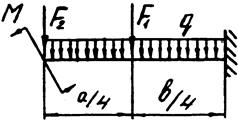
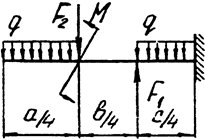
Задача 7. Консольная балка

Задача 7 (продолжение)

Задача 7 (окончание)

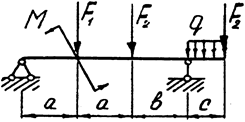
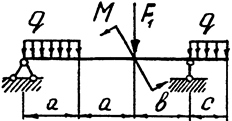
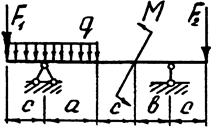
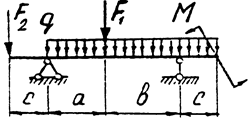
Задача 8. Двухопорная балка

Задача 8 (продолжение)

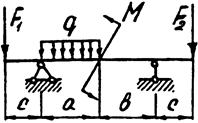
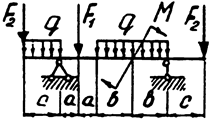
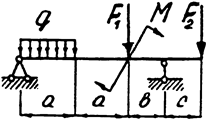
Задача 8 (окончание)

 

Приложение 1

 

ОБРАЗЕЦ ТИТУЛЬНОГО ЛИСТА

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ

ФЕДЕРАЦИИ

 

ФГБОУ ВПО

«УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

 

Кафедра ТМ ОЦБП

 

 

Курс «Сопротивление материалов»

 

 

РГР−1

Тема: Геометрические характеристики плоских сечений

 

Вариант - ___

 

Выполнил: студент_____________ (ФИО)

^{(подпись, дата)}

Проверил: преподаватель________ (ФИО)

^{(подпись, дата)}

 

 

Екатеринбург

Приложение 2

 

Пример решения задачи 1

 

 

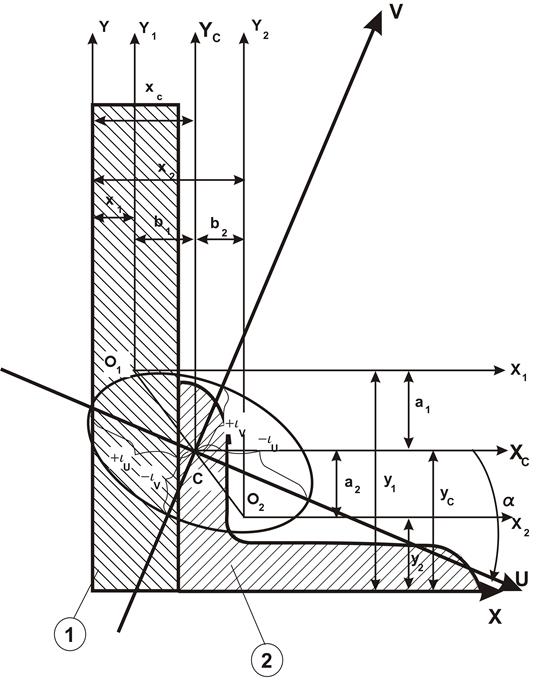
Дано: L

В=14 см, в=9 см, у₀=4,58, х₀=2,12, I_y=145,54 см⁴, I_x=444,45 см⁴, I_u=85,51 см⁴

I_xy=147 см⁴, tqa=0,409, А=22,24см²

Для прямоугольного сечения: h=2 см, в=15 см, А=30 см².

1. Определение координат центра тяжести все сложной фигуры (положение центральных осей)

_x

где х₁, у₁; х₂, у₂ – расстояние от центра тяжести каждого сортамента до

вспомогательных осей

 

 

2. Определение осевых моментов инерции относительно центральных осе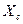й

и

,

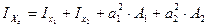
- расстояние от центра тяжести каждого сортамента до центральных осей.

Откладываем по оси

по оси

 

3. Определение центробежного момента инерции относительно центральных осе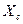й и :

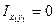, т.к. лист имеет горизонтальную ось симметрии, то собственные центральные оси листа являются главными

 

 

4. Определение моментов сопротивления относительно центральных осей 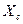и :

; , где

 

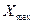, - расстояние от центра тяжести всей фигуры до наиболее удаленных точек по центральным осям

=

=

 

 

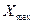5. Определение положения главных центральных осей угол наклона

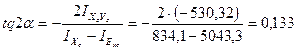
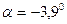, угол откладывается по часовой стрелке

Если угол имеет положительное значение, то откладывается против часовой стрелки.

6. Определение главных центральных моментов инерции относительно главных центральных осей:

 

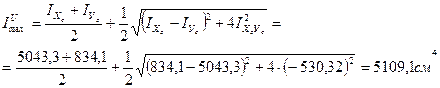
7. Определение моментов сопротивления относительно главных центральных осей :

 

 

8. Определение радиусов инерции относительно центра тяжести:

 

 

 

9. Проверка:

834,1+5043,3=5109,1+768,3

5877,4=5877,4(см⁴)

 

Пример решения задачи 2

 

1. Для определения внутренних усилий разбиваем стержень на отдельные участки, начиная от свободного конца.

Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечного сечения. Таким образом, заданный стержень имеет два участка.

Применяя метод сечения, будем оставлять нижнюю часть и отбрасывать верхнюю отсеченную часть стержня.

 

2. Определение реакции опоры в жесткой заделке в т.А:

 

3. Определение продольной силы в сечениях стержня методом сечения

Проведем произвольное сечение на участке I-I.

 

Сечение I-I

 

 

при

 

Сечение II-II

 

при

 

Построим эпюру, показывающую как меняется, по длине стержня. Для этого, проведя ось абсцисс графика параллельно оси стержня, откладываем в произвольном масштабе значения продольных сил по оси ординат. Полученный график принято штриховать, при этом штриховка должна быть перпендикулярна оси стержня.

 

4. Определение нормальных напряжений 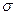, возникающих в сечениях стержня:

 

 

 

5. Определение удлинения (перемещения) сечений после деформации:

Эпюру перемещений следует строить от защемленного конца

 

6. Определение погрешности

 

Пример решения задачи 3

Дано:

Определить:

 

1. D l₁ – удлинение стержня 1

D l₂ – удлинение стержня 2

 

Из подобия треугольников D ОДД₁ и D ОСС₁

 

- уравнение совместности деформаций стержней. (1)

 

По закону Гука удлинения стержней определяются:

 

 

 

 

 

Выполним подстановки в уравнение (1), получим:

 

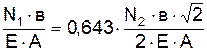, откуда

 

(2)

Заменим стержни 1 и 2 их реакциями ().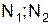

Составим уравнение статики:

 

 

Выполним подстановку в уравнение (2):

 

 

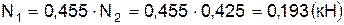
Проверка вычислений производим подстановкой в уравнения статики:

Расчет верен.

 

Расчет площади поперечного сечения стержня (№ 2):

 

Расчет площади поперечного сечения стержня (№1):

Расчет нормального напряжения в стержне (№1):

, т.е. 160 МПа – что допустимо.

Прочность обеспечена!

Пример решения задачи 4

 

Для данной схемы плоского напряженного состояния в элементе детали необходимо определить:

1. Главные напряжения и положение главных площадок.

2. Максимальное касательное напряжение.

3. Относительные деформации.

4. Удельную потенциальную энергию деформации.

Материал детали – сталь.

После определения главных площадок и главных напряжений их поло

жение и направление действия – нанести на заданную схему.

 

Дано:

 

1. Определение главных площадок и главных напряжений:

 

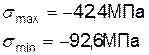
Максимальные касательные напряжения равны:

 

2. Относительные деформации заданной площадки определяются:

 

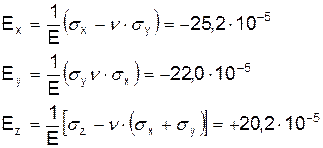
3. Удельная потенциальная энергия деформации заданной площадки:

 

4. Проверка вычислений:

 

Пример решения задачи 5

 

1. Определение реактивного момента в жесткой заделке в т. А:

 

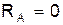
2. Определение внутренних крутящих моментов, возникающих в сечениях стержня:

 

	сечение I-I
	сечение II-II
	сечение III-III
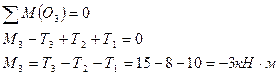
	сечение IV-IV

 

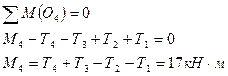
3. Определение диаметра вала из условия прочности при кручении:

 

3. Определение углов закручивания, возникающих в сечениях стержня:

, где

 

4. Определение относительного угла закручивания, возникающего на валу:

 

 

Пример решения задачи 6

 

 

Определить и построить эпюры:крутящих моментов - М_кр, поперечных сил Q, подобрать сечение двутавра.

1. Определение опорных реакций

 

 

Проверка

 

 

2. Определение внутренних силовых факторов методом сечений

 

		Сечение I-I
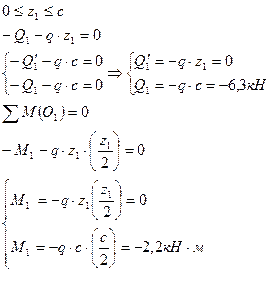
		Сечение II-II
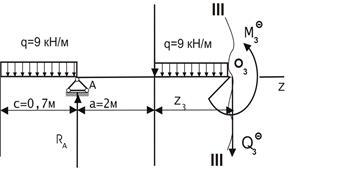
		Сечение III – III
	Сечение IV-IV
		Сечение V-V

3. Подбор сечения двутавровой балки

,

 

№ 16

 

 

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ

Система СИ

 

F —сосредоточенная сила (условно как бы приложенная в одной точке);

q — интенсивность распределенной нагрузки, сила на единицу длины (Н/м, МН/м);

М — внешний момент, действующий на элемент конструкции (изгибающий или крутящий);

g — удельный вес материала;

s — нормальное напряжение (сигма s);

t — касательное напряжение (тау t);

[s] — допускаемое нормальное напряжение;

[s]_р — допускаемое нормальное напряжение при растяжении;

[s]_сж — допускаемое нормальное напряжение при сжатии;

[t] — допускаемое касательное напряжение [t]» (0,5…0,6);

s₁, s₂, s₃ — главные напряжения (экстремальные нормальные);

s_max, t_max — максимальные напряжения;

s_а, t_a — напряжения по произвольной наклонной площадке;

n, n_у — коэффициенты запаса прочности и устойчивости;

N — продольная сила;

Q_x, Q_y — поперечные силы;

М_х, М_у – изгибающие моменты относительно осе Х и У;

М_кр — крутящий момент (относительно продольной оси Z);

Е — модуль упругости Юнга для широкого круга материалов (Е = 2∙10⁵ МПа);

G — модуль сдвига (G=8×10⁴ МПа);

m — коэффициент Пуассона;

s_t — предел текучести;

s_в — предел прочности;

s_пп — предел пропорциональности;

S_к — истинное сопротивление разрыву;

d — относительное продольное удлинение;

y — относительное поперечное сужение;

u — удельная потенциальная энергия деформации;

W — работа внешней силы;

g_ху, g_zx, g_уz — угловые сдвиговые деформации в разных плоскостях;

Dl — абсолютное продольное удлинение (или укорочение);

e₁, e₂, e₃ — главные относительные деформации;

e — относительное продольное удлинение (или укорочение);

j — угол закручивания поперечного сечения вала при кручении;

d — диаметр круглого стержня;

у — прогиб балки при изгибе;

z — координата произвольной точки сечения при рассечении по методу РОЗУ;

S_х, S_у — статические моменты площади сечения относительно осей Х и У;

А — площадь поперечного сечения стержней, балок и валов;

А₀ — первоначальная (до нагружения) площадь поперечного сечения образца растяжения;

х_с, у_с — координаты центра тяжести сечения;

х_i, у_i — координаты центров тяжести отдельных фигур сечения;

I_x, I_y — относительные моменты инерции относительно осей Х и У;

I_ху — центробежный момент инерции сечения относительно осей Х и У;

I_Р — полярный момент инерции сечения относительно координат;

i_х, i_у — главные радиусы инерции;

I_max,I_min — главные моменты инерции сечения;

W_х, W_у — осевые моменты сопротивления сечения (использются при расчете на прочность при изгибе)

W_Р — полярный момент сопротивления сечения (используется при расчете на кручение);

 

 

1 МПа = 1000 кН/м²

1 кН = 100 кг

Е = 2×10⁵ МПа = 2×10⁸ кН/м²

[s] = 160 МПа = 160000 кН/м²

А = 2 см² = 0,0002 м²