Рассмотрим многомерную линейную систему, описываемую уравнениями состояния и выхода:
 ,
,  ,
,
 .
.
Для линейных систем справедлив принцип суперпозиции: эффект, вызываемый суммой нескольких воздействий, равен сумме эффектов от каждого из воздействий в отдельности. Закон изменения вектора состояния линейной системы представляется в виде суммы свободного и вынужденного движений:  . Аналогичное соотношение справедливо и для вектора выхода:
. Аналогичное соотношение справедливо и для вектора выхода:  в силу связи (1.37).
в силу связи (1.37).
Свободное движение 
 происходит при отсутствии внешнего воздействия
происходит при отсутствии внешнего воздействия  вследствие ненулевых начальных условий (1.36). Оно определяется решением однородной системы уравнений, соответствующей исходному уравнению состояния (1.35):
вследствие ненулевых начальных условий (1.36). Оно определяется решением однородной системы уравнений, соответствующей исходному уравнению состояния (1.35):
 (1.43)
(1.43)
с начальными условиями  . Если начальные условия нулевые, свободное движение в системе отсутствует, т.е.
. Если начальные условия нулевые, свободное движение в системе отсутствует, т.е.  .
.
Вынужденное движение 
 — это реакция системы на внешнее воздействие
— это реакция системы на внешнее воздействие 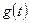 при нулевых начальных условиях. Оно определяется решением неоднородного уравнения (1.35) при нулевых начальных условиях.
при нулевых начальных условиях. Оно определяется решением неоднородного уравнения (1.35) при нулевых начальных условиях.
Для многомерных нестационарных систем, описываемых соотношениями (1.35) — (1.37), законы изменения векторов состояния и выхода определяются по формулам
 , (1.44)
, (1.44)
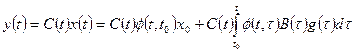 , (1.45)
, (1.45)
где  — переходная матрица, или матрица Коши, являющаяся решением уравнения
— переходная матрица, или матрица Коши, являющаяся решением уравнения
 (1.46)
(1.46)
начальным условием
 . (1.47)
. (1.47)
Первые слагаемые в (1.44), (1.45) описывают свободное движение, а вторые вынужденное.
Формулы (1.43) — (1.46) следуют из общего алгоритма решения линейных систем обыкновенных дифференциальных уравнений [40], включающего три этапа.
Первый этап. Решается однородная система дифференциальных уравнений
 ,
,
соответствующая исходной неоднородной системе
 .
.
Ее общее решение записывается в форме
 ,
,
где  вектор произвольных постоянных,
вектор произвольных постоянных,  — фундаментальная матрица,
— фундаментальная матрица,  линейно независимые решения однородной системы. Каждый столбец
линейно независимые решения однородной системы. Каждый столбец  (фундаментальной матрицы удовлетворяет однородной системе, т.е. справедливы равенства
(фундаментальной матрицы удовлетворяет однородной системе, т.е. справедливы равенства  ,
,  или
или  .
.
Второй этап. Ищется общее решение неоднородной системы методом вариации произвольных постоянных:
 ,
,
где вектор-функция  подлежит определению. Подставляя
подлежит определению. Подставляя  в неоднородную систему, получаем
в неоднородную систему, получаем
 .
.
С учетом  имеем
имеем
 или
или  .
.
Обратная матрица  существует, поскольку
существует, поскольку  как определитель Вронского. Интегрируя последнее соотношение, находим
как определитель Вронского. Интегрируя последнее соотношение, находим
 ,
,
где  — вектор произвольных постоянных. В результате искомое общее решение имеет вид
— вектор произвольных постоянных. В результате искомое общее решение имеет вид
 .
.
Третий этап. Ищется частное решение неоднородной системы, удовлетворяющее начальным условиям  :
:
 .
.
Отсюда  и
и
 .
.
Обозначая  , получаем формулу (1.44). При
, получаем формулу (1.44). При  получаем начальное условие (1.47). Умножая уравнение
получаем начальное условие (1.47). Умножая уравнение  справа на матрицу
справа на матрицу 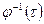 , имеем
, имеем  , т.е. уравнение (1.46).
, т.е. уравнение (1.46).
З а м е ч а н и е. Для многомерных стационарных систем, описываемых уравнениями
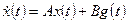 , (1.48)
, (1.48)
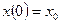 , (1.49)
, (1.49)
 , (1.50)
, (1.50)
законы изменения вектора состояния и вектора выхода находятся по формулам
 , (1.51)
, (1.51)
 , (1.52)
, (1.52)
где  — переходная матрица стационарной системы, зависящая от разности
— переходная матрица стационарной системы, зависящая от разности  . В данном случае решение уравнения (1.46) имеет вид
. В данном случае решение уравнения (1.46) имеет вид
 .
.
Анализ выходных процессов
ПОСТАНОВКА ЗАДАЧИ
Пусть известны:
а) входной сигнал 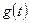 (см. разд. 1.2.1);
(см. разд. 1.2.1);
б) система, описываемая уравнениями состояния и выхода
 ,
,  ,
,
 ;
;
в) вектор начальных состояний  (см. разд. 1.2.1).
(см. разд. 1.2.1).
Требуется найти законы изменения вектора состояния  и вектора выхода
и вектора выхода 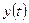 .
.
З а м е ч а н и е. Если система образована соединениями подсистем, то она заменяется эквивалентной системой так, как показано в разд. 1.2.2.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1. Найти переходную матрицу (одним из трех способов, рассмотренных далее).
2. Используя соотношения (1.44), (1.45) или (1.51), (1.52) в зависимости от типа системы, определить законы изменения векторов состояния и выхода.
Рассмотрим различные способы нахождения переходной матрицы.
Первый способ. Если фундоменальная матрица  , столбцы которой образуют фундаментальную систему решений однородной системы дифференциальных ураннений (1.43), известна, то переходная матрица находится по формуле
, столбцы которой образуют фундаментальную систему решений однородной системы дифференциальных ураннений (1.43), известна, то переходная матрица находится по формуле
 , (1.53)
, (1.53)
З а м е ч а н и е. Общее решение однородной системы (1.43) можно записать в виде
 , (1.54)
, (1.54)
где  — произвольные постоянные
— произвольные постоянные
Для стационарных систем следует выполнить действия:
1. Найти корни характеристического уравнения
 , (1.55)
, (1.55)
где  — единичная матрица.
— единичная матрица.
2. Выписать выражение общего решения (1.54) для каждой компоненты вектора х, следуя известным правилам в зависимости от типа корней (см. разд. 1.1.4). При этом произвольные постоянные в выражениях различны.
3. Полученные выражения подставить в однородную систему. Во многих случаях достаточно подставить в первые 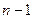 уравнений системы, что облегчает решение задачи.
уравнений системы, что облегчает решение задачи.
4. Приравнять коэффициенты при одинаковых функциях аргумента t и решить полученную систему уравнений.
5. Выписать общее решение, зависящее от n произвольных постоянных в форме (1.54). В результате находится фундаментальная матрица, а по формуле (1.53) — переходная.
Пример 1.21. Найти переходную матрицу системы, описываемой дифференциальными уравнениями
 ,
,
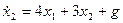 .
.
□ Составим матрицу системы  . Используем приведенный выше
. Используем приведенный выше
алгоритм.
1. Корни характеристического уравнения  ,
,  действительные разные:
действительные разные:  ,
,  .
.
2. Запишем выражения общего решения для каждой компоненты:
 ,
,
 .
.
3. Подставим полученные соотношения в первое уравнение системы:
 .
.
4. Приравняв коэффициенты при  и
и  , получим
, получим
 , или
, или  ,
,
 ,
,  .
.
5. Из пп. 2, 4 имеем
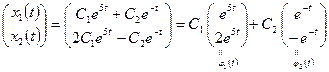 .
.
Отсюда
 ,
, 
и по формуле (1.53)

 .
.
Пример 1.22. Найти переходную матрицу системы, описываемой дифференциальными уравнениями
 ,
,
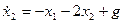 .
.
□ Составим матрицу системы  . Используем приведенный выше алгоритм.
. Используем приведенный выше алгоритм.
1. Корень характеристического уравнения  ,
,  действительный кратный:
действительный кратный:  ,
,  .
.
2. Выражения общего решения для каждой компоненты имеют вид
 ,
,
 .
.
3. Подставим полученные соотношения в первое уравнение системы:
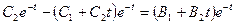 .
.
4. Приравняв коэффициенты при  и
и  , получим
, получим
 ,
,
 .
.
5. Из пп. 2, 4 имеем
 .
.
Отсюда находится фундаментальная матрица
 ,
, 
и по формуле (1.53)

 .
.
В случае нестационарных систем для определения фундаментальной матрицы можно воспользоваться следующим приемом, позволяющим уменьшить порядок системы, если известно ее решение  и
и  при
при  .
.
Тогда вектор-функции  ,
,  , образующие вместе с функцией
, образующие вместе с функцией  фундаментальную систему решений для (1.43), можно найти по формулам
фундаментальную систему решений для (1.43), можно найти по формулам
 ,
,
…
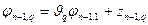 ,
,  , (1.56)
, (1.56)
 ,
,
где
 ,
,
а функции  ,
,  являются линейно независимыми решениями системы
являются линейно независимыми решениями системы  порядка
порядка
 ,
,  . (1.57)
. (1.57)
Пример 1.23. Найти переходную матрицу системы, описываемой дифференциальными уравнениями
 ,
,
 .
.
□ Для определения переходной матрицы  нужно найти два линейно независимых решения заданной системы. Первое решение будем искать с помощью рядов, представляя функции
нужно найти два линейно независимых решения заданной системы. Первое решение будем искать с помощью рядов, представляя функции  ,
,  в виде
в виде
 ,
, 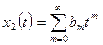 .
.
Подставив эти функции в систему, предварительно умножив первое уравнение на  , а второе — на
, а второе — на  , имеем
, имеем
 ,
,
 .
.
Приравнивая коэффициенты при одинаковых степенях  , получаем
, получаем


 ,
,  ,
,
 .
.
Данной системе уравнений удовлетворяют коэффициенты:
 ,
,  ,
, 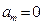 ,
,  ;
;
 ,
,  ,
, 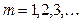 .
.
Таким образом, вектор-функция  является решением системы.
является решением системы.
Обозначим это решение  . Так как
. Так как  при всех
при всех  , можно понизить порядок системы. Согласно (1.56) второе решение
, можно понизить порядок системы. Согласно (1.56) второе решение  ищется в виде
ищется в виде
 ,
,  ,
,
где  , а
, а  - решение системы (1.57), которая в данном случае состоит из одного уравнения
- решение системы (1.57), которая в данном случае состоит из одного уравнения  :
:
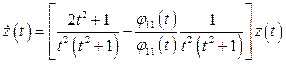 .
.
Подставляя  и
и  , получаем уравнение
, получаем уравнение
 ,
,
решение которого находится с помощью разделения переменных, т.е.  . В результате
. В результате  . Тогда
. Тогда  и, следовательно,
и, следовательно,  ,
,  .
.
По найденным решениям 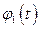 и
и  составляем фундаментальную матрицу
составляем фундаментальную матрицу
 и
и  .
.
По формуле (1.53) имеем

Второй способ. Применение теоремы разложения Сильвестра [60]. Переходная матрица стационарной системы определяется по формуле
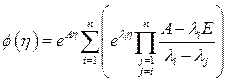 , (1.58)
, (1.58)
Где 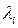 - собственные значения матрицы
- собственные значения матрицы  (здесь предполагается, что они различны), a
(здесь предполагается, что они различны), a  - единичная матрица.
- единичная матрица.
Пример 1.24. Найти законы изменения векторов состояния и выхода многомерной системы:
 ,
, 
с начальными условиями  ,
,  , при входном сигнале
, при входном сигнале

1. Перепишем уравнения системы в матричной форме:
 ,
,  .
.
2. Найдем переходную матрицу. Для этого определим собственные значения матрицы  . Получим
. Получим
 ,
,  .
.
Отсюда  ,
,  . По формуле (1.58) имеем
. По формуле (1.58) имеем

 .
.
3. По формулам (1.51), (1.52) найдем законы изменения векторов состояния и выхода:

 ,
,

 .
.
Пример 1.25. Найти законы изменения векторов состояния и выхода многомерной системы:


с начальными условиями  ,
,  при входном сигнале
при входном сигнале
 ,
,  .
.
1. Перепишем уравнения системы в матричной форме:
 ,
,  .
.
2. Найдем переходную матрицу. Для этого определим собственные значения матрицы  . Получим
. Получим
 ,
,  .
.
Отсюда  ,
,  . По формуле (1.58) имеем
. По формуле (1.58) имеем

 ,
,
так как  ,
,  .
.
3. Mo формулам (1.51), (1.52) найдем законы изменения векторов состояния и выхода:

 ,
,
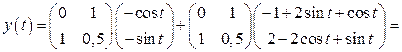
 .
.
Третий способ. Использование теоремы Кели-Гамильтона [60].
Рассмотрим два случая ее применения.
1. В случае различных собственных значений матрицы  :
:
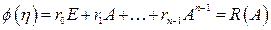 (1.59)
(1.59)
где  — число строк матрицы
— число строк матрицы  ;
;  —
—  — я степень матрицы
— я степень матрицы  ; коэффициенты
; коэффициенты  многочлена
многочлена  находятся из системы уравнений
находятся из системы уравнений
 ,
,  . (1.60)
. (1.60)
2. В случае кратных собственных значений матрицы  формула (1.59) также справедлива. Корню
формула (1.59) также справедлива. Корню  кратности
кратности  в системе
в системе  уравнений (1.60) соответствуют соотношения
уравнений (1.60) соответствуют соотношения
 ,
,  . (1.61)
. (1.61)
Пример 1.26. Найти переходную матрицу системы, если матрица  в уравнении состояния имеет вид
в уравнении состояния имеет вид  (см. пример 1.24).
(см. пример 1.24).
□ Собственные значения матрицы  :
:  ,
,  различны,
различны,  . Поэтому составим систему уравнений (1.60):
. Поэтому составим систему уравнений (1.60):
 .
.
Отсюда  ,
,  . По формуле (1.59) имеем
. По формуле (1.59) имеем

 .
.
Результат совпадает с полученным ранее.■
Пример 1.27. Найти законы изменения векторов состояния и выхода многомерной системы:


с начальными условиями 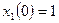 ,
,  при входном сигнале
при входном сигнале

□ Перепишем уравнения системы в матричной форме:
 ,
,  ,
,
где  ,
,  ,
,  .
.
2. Найдем переходную матрицу. Для этого определим собственные шачения матрицы  . Получим
. Получим
 ,
,  .
.
Отсюда  (корень действительный кратный). По формуле (1.61) имеем
(корень действительный кратный). По формуле (1.61) имеем
 т.е.
т.е. 
Отсюда  ,
,  . По формуле (1.59) получаем
. По формуле (1.59) получаем

 .
.
3. По формулам (1.51), (1.52) найдем законы изменения векторои состоя ния и выхода:

 ,
,

 .
.






