Лекция №9
Тема: Уравнение прямой и плоскости в пространстве. Условие параллельности и перпендикулярности прямых и плоскостей.
План.
1. Угол между двумя прямыми.
2. Условие параллельности.
3. Условие перпендикулярности.
4. Общее уравнение прямой.
Пусть заданы две прямые 
и 
(рис. 17). Тогда
, 
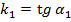, и угол между этими прямыми 
равен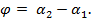 
Тогда 
= 
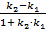иформула угла между прямыми имеет вид
Условие параллельности двух прямых.
Если две прямые и параллельны, то угол между ними равен нулю и тогда
Следовательно, 
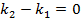, или 
.
Таким образом, необходимым и достаточным условием параллельности прямых является равенство их угловых коэффициентов 
(рис. 18).
Пример 8. Прямые 
и 
являются параллельными т.к. 
Условие перпендикулярности двух прямых.
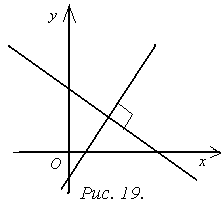Если две прямые и взаимно перпендикулярны (рис. 19), то угол между ними равен 
и 
не существует. А так как
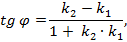и дробь
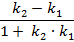
не существует тогда и только тогда, когда её знаменатель равен нулю, т.е. тогда, когда выполняется равенство 
. Это и есть условие перпендикулярности двух прямых. Выразив один угловой коэффициент через другой, получим
Пример 9. Прямые
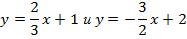
перпендикулярны, так как
Общее уравнение прямой.
Уравнение вида 
называется общим уравнением прямой.
а) Если 
,то уравнение будет иметь вид 
. Прямая, определяемая этим уравнением, проходит через начало координат, так как координаты 
удовлетворяют этому уравнению.
б) Если 
,то уравнение примет вид 
или
Уравнение не содержит переменной 
, а определяемая этим уравнением прямая, параллельна оси 
.
в) Если 
, то уравнение примет вид 
, откуда
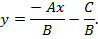
Обозначим
получим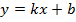 
- уравнение прямой через угловой коэффициент 
.
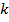Уравнение прямой в полярных координатах.
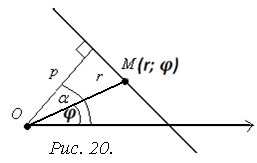Пусть дана система полярных координат 
с полюсом в точке 
и прямая, проходящая на расстоянии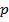 
от полюса (рис. 20).Выберем на прямой произвольную точку 
с текущими координатами . Тогдаиз прямоугольного треугольника получим равенство 
или ввиду четности функции косинуса
Это и есть уравнение прямой в полярных координатах.
Нормальное уравнение прямой.
Так как уравнение прямой в полярных координатах имеет вид
где 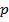- расстояние от полюса до прямой, то разложив косинус, получим
Учитывая формулы перехода от полярных координат к декартовым 
, 
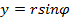, получим уравнение прямой в виде
которое и называется нормальным (рис. 21).
Замечание. Чтобы общее уравнение прямой записать в нормальном виде необходимо его разделить на выражение 
. Тогда оно примет вид
Заменив
получим уравнение в нормальном виде.
Пример 10. Записать уравнение прямой линии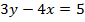 
в нормальном виде.
Решение. Запишем уравнение в общем виде, перенеся все слагаемые в одну сторону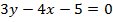 
. Разделим обе части уравнения на выражение 
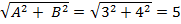. Получим
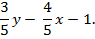
Так как
то это и есть нормальное уравнение прямой.
