Метод сил в расчетах статически неопределимых систем

Общие сведения о статически неопределимых системах. Степень статической неопределимости

 

При изучении курса сопротивления материалов уже приходи­лось встречаться с расчетом статически неопределимых систем, т. е. та­ких, для определения внутренних усилий в которых недостаточно одних лишь уравнений статики: требовалось еще составлять дополнительные уравнения — уравнения деформаций (перемещений).

Характерной особенностью статически неопределимых систем (в отличие от статически определимых) является то, что распределение усилий в них зависит не только от внешних сил, но и от соотношений между поперечными размерами отдельных элементов. Если элементы системы изготовлены из различных материалов, то распределение усилий зависит также от модулей упругости этих материалов. Другая особенность — смещение опор, тем­пературные воздействия и неточность сборки конструкции обычно вызывают появление в таких системах дополнительных усилий, чего не происходит в статически определимых системах.

Расчет статически неопределимой системы начинается с анализа ее схемы. Анализ необходим, прежде всего, для того, чтобы установить сте­пень статической неопределимости.

Степень статической неопределимости равна числу так называемых лиш­них связей, удаление которых превращает статически неопределимую сис­тему в определимую геометрически неизменяемую систему.

Связью в строительной механике называется всякое препятствие, не допускаю­щее изменения взаимного положения точек или сечений системы. Термин «лишняя связь» следует понимать как «избыточная связь», а не как «ненужная связь».

Геометри­чески неизменяемой называется такая система, изменение фор­мы которой возможно лишь в связи с деформациями ее элементов.

Статически определимая система не имеет лишних связей; удаление из нее хотя бы одной связи превращает ее в геометрически изменяемую систему, т.е. в механизм. Балка является системой статически неопределимой один раз (или однажды), если один из опорных стержень­ков представляет собой лишнюю (избыточную) связь ее с землей (с основани­ем). Отбросив один опорный стержень или включив в балку один шарнир, получим статически определимую, геометрически неиз­меняемую систему.

Прямоугольная замкнутая рама является системой трижды статически неопределимой, так как для превращения ее в статически определимую необходимо, например, перерезать один из ее элементов и тем самым устранить три лишние внутренние связи.

Реакциями этих внутренних связей являются: продольная сила, поперечная сила и изгибающий момент, действующие в месте разреза. Эти реакции при помощи уравнений статики не могут быть найдены. В аналогичных условиях в смысле статической неопределимости находится любая система, представ­ляющая замкнутый контур, который всегда трижды статически неопределим.

Примером сооружения с одним замкнутым контуром является система, изобра­женная на рис. 1. Бесшарнирная рама также представляет собой замк­нутый контур; он ограничен снизу землей, которую можно рассматривать как бесконечно жесткий стержень.

 

 

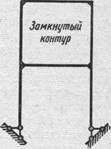
Рис. 1

Рис.2 2

В рамной конструкции, представленной на рис. 2, а, верхний контур снабжен шарниром; в разрезе, проведенном по этому шарниру, действуют только два внутренних усилия: N и Q (рис. 2, 6). Такой контур дважды ста­тически неопределим. Если рассматривать всю систему в целом, то она пять раз статически неопределима, так как нижний контур рамы замкнутый и, следовательно, неопределим трижды. Систему, освобожденную от внутренних лишних связей, можно представить в виде двух защемленных внизу стержней с горизонтальными консолями (рис. 2, 6).

К выяснению степени статической неопределимости этой системы можно подойти и несколько иначе. Верхний контур рамы, имеющий один внутрен­ний шарнир, дважды статически неопределим (имеет две лишние связи). Кроме того, каждая из заделок дает три составляющих опорной реакции (две силы и момент), т. е. на раму наложено шесть внешних связей, а урав­нений статики для плоской системы можно составить лишь три. Следова­тельно, три внешние связи являются лишними, а всего имеется пять лишних связей, т. е. система пять раз статически неопределима.

Необходимо заметить, что исключение лишних связей для превращения одной и той же статически неопределимой конструкции в статически опре­делимую, может быть произведено различными способами, однако число отбрасываемых связей всегда будет одно и то же.

Включение шарнира в узел рамы, в котором сходятся два стержня, или же постановка его в любое место на оси стержня нарушает (снимает) одну связь и снижает общую степень статической неопределимости системы на единицу. Такой шарнир будем называть одиночным, или простым.

При удалении связей системы необходимо следить за тем, чтобы получае­мая конструкция была геометрически неизменяема. С этой точки зрения в раме, показанной на рис. 3, имеющей одно лишнее опорное закрепление, было бы ошибочным удаление вертикального стерженька, так как оставшиеся три опорных стерженька пересекались бы в точке А и, сле­довательно, не могли бы препятствовать повороту рамы вокруг этой точки. Правильным будет вариант удаления лишнего горизонтального стерженька.

 

 

Рис. 3

 

Для конструкций со сложным внутренним образованием можно указать на следующий общий прием определения степени статической неопредели­мости. В его основу кладется то соображение, что каждый шарнир, включен­ный в узел, соединяющий К стержней, снижает степень статической неопре­делимости на К — 1, так как такой шарнир заменяет К — 1 одиночных шарниров. Поэтому для определения степени статической неоп­ределимости конструкции необходимо взять утроенное количество замкну­тых контуров (предполагая, что все шарниры, в том числе и опорные, заме­нены жесткими соединениями) и затем уменьшить его на число включенных в конструкцию одиночных шарниров, учитывая при этом, что один общий шарнир эквивалентен К — 1 одиночным шарнирам. Представив это правило в виде формулы, получим:

n = 3m — Ш.

Здесь n — степень статической неопределимости системы; m — число замкнутых контуров в конструкции в предположении отсутствия шарнир­ных соединений; Ш — число одиночных шарниров; шарнир, соединяющий два стержня, считается за один (одиночный шарнир), соединяющий три стержня — за два одиночных шарнира (двойной шарнир) и т. д_.

Плоскую статически неопределимую систему, имеющую более трех опорных стержней, можно рассматривать как внешне, как внутренне или как одновременно внешне и внутренне статически неопределимую — в зависимости от того, какие связи этой системы считать лиш­ними. Так, например, один раз статически неопределимую раму, изображен­ную на рис. 3, можно рассматривать как внешне статически неопредели­мую, если за лишнюю связь считать правый горизонтальный опорный стер­жень, т. е. если превратить ее в статически определимую систему путем удаления этого стержня. Если же лишней считать связь, препятст­вующую повороту одной части ригеля рамы относительно другой, т. е. пре­вратить раму в статически определимую систему путем постановки шарнира в ригеле, то тогда раму надо рассматривать как внутренне стати­чески неопределимую.

 

ОСНОВНАЯ СИСТЕМА МЕТОДА СИЛ

 

Расчет статически неопределимой системы методом сил начинается с определения степени статической неопределимости. Далее нужно выбрать основную систему.

Основная система получается из заданной путем отбрасывания лишних связей. Вместо отброшенных связей прикладываются реакции этих связей. Они называются лишними неизвестными и определяются в процессе расчета статически неопределимой системы.

Основное требование, предъявляемое к основной системе: она должна быть геометрически неизменяемой и статически определимой.

Обычно для заданной системы можно образовать несколько вариантов основной системы. Для расчета выбирают наиболее удобный вариант.

 

КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ

 

Как было указано выше, определение усилий в стати­чески неопределимой системе связано с необходимостью составления до­полнительных уравнений — уравнений деформаций (перемещений) системы. Для этого прежде всего следует превратить заданную п раз стати­чески неопределимую систему в статически определимую, устранив из нее лишние связи. Полученная таким путем статически определимая система называется основной.

Устранение каких-либо связей не изменяет внутренних усилий, возни­кающих в системе, и ее деформаций, если к ней прикладываются дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Поэтому, если к основной системе, кроме заданной нагрузки, приложить реакции устраненных связей, то основная и заданная системы станут эквивалентными.

В заданной системе в направлениях имеющихся жестких связей (в то числе и тех связей, которые отброшены при переходе к основной системе) перемещений быть не может. Поэтому в основной системе перемещения по направлениям отброшенных связей должны быть равны нулю. Следовательно реакции отброшенных связей должны иметь такие значения, при ксторых перемещения по их направлениям равнялись бы нулю.

Условие равенства нулю перемещения по направлению любой из отброшенных связей на основании закона независимости действия сил может быть представлено в следующем виде:

Δ_i = Δ_i1 + Δ_i2 +... +Δ_{i , n-1} + Δ_{i n} + Δ_{i p} = 0.

Здесь первые индексы означают направление перемещения (и одновременно номер отброшенной связи), а вторые указывают на причины, вызвавшие перемещение. Таким образом, слагаемое Δ_ik следует читать: «перемещение по направлению связи i, вызванное действием реакции связи k» Слагаемое Δ_ip означает перемещение по направлению связи i, вызванное действием заданной нагрузки.

Обозначив величину реакции связи k (в виде силы или момента) через X_k и выразив перемещения Δ_ik через единичные перемещения с помощью равенства Δ_ik = X_kδ_ik, представим условие так:

Δ_i = X₁ δ_{i 1} + X₂ δ_{i 2} + … + X_n δ_{i n} + Δ_{i p} = 0.

Таким образом, условие эквивалентности основной и заданной систем математически сводится к удовлетворению системы n линейных уравнений.

 

Главная Побочные диагонали

 

Эти уравнения являются теми дополнительными уравнениями деформаций (перемещений), которые позволяют раскрыть статическую неопределимость заданной системы. Первое из этих уравнений выражает мысль о равенстве нулю перемещения в основной системе по направлению первой отброшенной связи (по направлению силы или момента), второе — по направлению второй отброшенной связи и т. д.

Уравнения называются каноническими уравнениями метода сил. Такое название указывает, во-первых, на то, что уравнения составляются по определенному правилу (канону), и, во-вторых, на то, что неизвестными в уравнениях являются силы, представляющие собой реакции отброшенных связей. Число уравнений равно числу отброшенных связей, т.е. степени статической неопределимости заданной системы.

Следует заметить, что вид канонических уравнений, т. е. количество слагаемых в каждом из них и общее число этих уравнений, определяется лишь степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

Можно установить следующий порядок расчета статически неопределимых систем:

1. Выбирается основная статически оп­ределимая система путем отбрасывания в заданной системе лишних связей.

2. Действие отброшенных связей возме­щается приложением к основной системе неизвестных усилий (сил или моментов).

3. Составляются канонические уравне­ния, выражающие ту мысль, что пол­ные перемещения в основной системе, возникающие по направлениям неизвестных усилий под влиянием этих усилий и нагрузки, равны нулю.

4. Основная система поочередно нагружается единичными усилиями X₁ = 1, Х₂ = 1, …, Х_п = 1 и от каждого из них отдельно строятся еди­ничные эпюры изгибающих моментов M_i. Помимо этого, строится грузовая эпюра изгибающих моментов М_р в основной системе метода сил.

5. Перемножением единичных эпюр вычисляются все коэффициенты δ_ik системы канонических уравнений.

6. Перемножением единичных и грузовой эпюр определяются грузовые члены Δ _ip системы канонических уравнений.

7. Решается система канонических уравнений, в результате чего находятся значения неизвестных Х₁, Х₂, …, Х_n.

8. Для получения окончательной (суммарной) эпюры изгибающих моментов ординаты каждой из единичных эпюр умножаются на найденное значение соответствующего неизвестного и все результаты суммируются (по отдельным точкам осей системы) с добавлением к ним ординат грузовой эпюры моментов. В ходе расчета выполняются проверки.

 

МАТРИЧНАЯ ФОРМА МЕТОДА СИЛ

 

Запишем канонические уравнения метода сил для n раз статически неопределимой системы:

δ₁₁ X₁ + δ₁₂ X₂ + … +δ_1n X_n + Δ_1p = 0

δ₂₁ X₁ + δ₂₂ X₂ + … +δ_2n X_n + Δ_2p = 0

.

.

.

δ_n1 X₁ + δ_n2 X₂ + … +δ_nn X_n + Δ_np = 0

Эту систему уравнений можно записать в виде одного матричного уравнения:

δ₁₁ δ₁₂ … +δ_1n X₁ Δ_1p

δ₂₁ δ₂₂ … +δ_2n X₂ Δ_2p

... +. = 0

...

...

δ_n1 δ_n2 … +δ_nn X _n Δ_np

 

Введем обозначения:

δ₁₁ δ₁₂ … δ_1n

δ₂₁ δ₂₂ … δ_2n – матрица коэффициентов

А_δ =... канонических уравнений

δ_n1 δ_n2 … δ_nn

 

Ее свойства:

1. Является квадратной симметричной.

2. Все элементы, стоящие на главной диагонали, являются положительными величинами.

Х₁

₌ Х₂ – матрица-столбец (вектор) лишних неизвестных

…

Х_n

 

Δ_1р

_р = Δ_2р – матрица-столбец (вектор) свободных членов

… канонических уравнений

Δ_np

 

 

А_δ × + 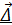_р = 0 (*) – матричная форма записи канонических уравнений

метода сил

Умножим равенство (*) на обратную матрицуА_δ^-1:

А_δ^-1 × А_δ × + А_δ^-1 × _р = 0

А_δ^-1 × А_δ – единичная матрица

Е =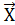

Отсюда вектор лишних неизвестных:

= – А_δ^-1 × _р

Элементами матрицы А_δ являются перемещения. Эту матрицу можно найти по следующей формуле:

А_δ = L_x^T BL_x,

где L_x – матрица изгибающих моментов в основной системе от единичных значений лишних неизвестных, т.е. от сил X₁ = 1, Х₂ = 1, …, Х_п = 1;

L_x^T – транспонированная по отношению к L_x матрица;

В – матрица податливости системы.

Вектор _р также можно определить по матричной формуле:

_р = L_xВ _р,

где _р – вектор изгибающих моментов в основной системе от внешней нагрузки.

Тогда:

= – (L_x^T BL_x)^-1×L_x^T B _р.

После определения вектора можно найти изгибающие моменты для заданной системы по следующей формуле:

= _р + L_x× ,

где – изгибающий момент для заданной системы.

Полученные формулы применяются при расчете рам методом сил с помощью ЭВМ.

Исходными для расчета являются следующие три матрицы: L_x, В, _р.

 

РАСЧЕТ РАМ МЕТОДОМ СИЛ С ПОМОЩЬЮ ЭВМ

 

Порядок расчета:

1. Определить степень статической неопределимости и выбрать основную систему.

2. Разбить раму на участки, нанести и пронумеровать сечения и выбрать правило знаков изгибающих моментов.

3. Построить эпюры изгибающих моментов в единичных и грузовом состояниях основной системы.

4. По единичным эпюрам составить матрицу L_x. Число строк в этой матрице равно числу сечений, а число столбцов равно числу единичных состояний основной системы.

5. По грузовой эпюре составить вектор _р.

6. Составить матрицы податливости для отдельных участков рамы, а затем для рамы в целом (матрица В).

7. С помощью ЭВМ (программа RAMS) найти вектор и построить эпюру изгибающих моментов для заданной системы.

8. Выполнить первую статическую проверку (SМ_уз = 0).

9. Построить эпюры поперечных сил Q и продольных сил N.

10. Выполнить вторую статическую проверку, т.е. проверку равновесия рамы в целом (SХ = 0; SУ = 0).

Примечание. Кинематическая проверка (проверка отсутствия перемещений по тем направлениям, где они заведомо отсутствуют) выполняется в процессе расчета самой ЭВМ.