Мосты для измерения индуктивности. Измерение емкости и индуктивности в основном производится с помощью мостов переменного тока. Они обеспечивают высокую точность чувствительности при относительной простоте.
Для измерения индуктивности и добротности катушек применяются схемы, показанные на (рис. 7.7). Схема (рис. 7.7 а) используется при малых добротностях (Q < 30), а схема (рис. 7.7 б) — при больших добротностях (Q > 30). Измеряемая катушка с индуктивностью Lx и сопротивлением Rx включается в первое плечо моста, образцовый конденсатор C 4 и переменный резистор R 4 — в противоположное плечо. Еще одним переменным элементом является резистор R 3. Резистор R 4 может быть включен либо параллельно (см. рис. 7.7 а), либо последовательно (см. рис. 7.7 б) с образцовым конденсатором C 4. Питание осуществляется от источника переменного тока G. В соответствии с равенством комплексных сопротивлений плеч (Z1Z4 = Z2Z3) запишем условие равновесия моста для (рис. 7.7 а):
(Rx + j ω Lx)[1 / (1 / R 4 + j ω C 4)] = R 2 R 3, (7.6)
где ω — частота напряжения питания; j — показатель мнимой составляющей комплексного сопротивления; R 2, R 3 и R 4 — плечи моста.
Разделение действительных и мнимых составляющих уравнения приводит к соотношениям
Rx = R 2 R 3/ R 4; (7.7)
и
Lx = C 4 R 2/ R 3. (7.8)
В уравнения (7.7) и (7.8) не входит частота, следовательно, мост может быть уравновешен, даже если форма кривой питающего напряжения не чисто синусоидальная. Добротность катушки определяется по формуле
Qx = ω Lx / Rx = ω C 4 R 4.
При фиксированной частоте напряжения питания ω и постоянной емкости C 4 шкалу переменного тока резистора R 4 можно проградуировать в значениях добротности Qx.
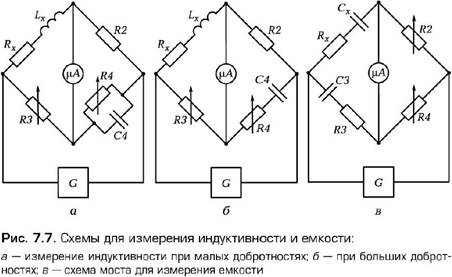
Схеме моста, представленной на (рис. 7.7 б), соответствует следующее условие равновесия:
(Rx + j ω Lx)[ R 4 + 1 / (j ω C 4)] R 2 R 3. (7.9)
Условие равновесия (7.9) соответствует системе уравнений
RxR 4 + Lx / C 4 = R 2 R 3;
ω Lx + R 4 = R 4/ (ω C 4),
решение которой относительно Rx и Lx имеет следующий вид:
Rx = ω2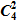 
R 2 R 3 R 4/ [1 + (ω C 4 R 4) 2 ]; (7.10)
Lx = C 4 R 2 R 3/ [1 + (ω C 4 R 4) 2 ] (7.11)
и
Qx = ω Lx / Rx = 1 / (ω C 4 R 4).
Итак, шкала переменного резистора R 4 снова может быть отградуирована в значениях добротностиQx.
В отношения (7.10) и (7.11) для Rx и Lx входит частота, поэтому мост является частотнозависимым. Равновесие имеет место только при некоторой частоте ω питающего напряжения. Если ее изменить, то равновесие нарушится.
Мосты для измерения емкости. При измерении емкости используется схема с образцовым конденсатором C 3 и переменными резисторами R 2 и R 4 (см. рис. 7.7 в). Исследуемый конденсатор в этой схеме представлен (замещен) последовательным соединением емкости Cx и активного сопротивления Rx. Введение Rx необходимо в связи с наличием потерь в конденсаторе. Питание осуществляется от источника переменного тока G. Условие равновесия имеет вид
Rx = R 2 R 3/ R 4, (7.12)
и
Cx = C 3 R 4/ R 2. (7.13)
Принято характеризовать потери в конденсаторе значением тангенса угла потерь tgδ, который в случае последовательной схемы замещения связан с Rx соотношением
tgδ = ω CxRx.
С учетом условий (7.12) и (7.13) это соотношение можно записать следующим образом:
tgδ = ω R 3 C 3.
Контрольные вопросы
1 Каким способом измеряется индуктивность катушек?
2 Чем различаются мосты для измерения малых и больших значений добротности катушек?
3 Как измерить добротность катушек?
4 Каким прибором можно измерить тангенс угла потерь конденсатора?
5 Как измеряется добротность катушек?
6 Какова схема двойного моста и для каких измерений он применяется?
