Делимость и остатки
Введение
Принято считать, что арифметика предшествует алгебре, что это «более элементарная» часть математики. В школе арифметике учат, начиная с первого класса, а алгебре – только с пятого. Поскольку подавляющее большинство людей знает о математике главным образом то, что они услышали в школе на уроках, то мнение об элементарности арифметики глубоко укоренилось. Между тем, арифметика, если ее понимать как учение о свойствах целых чисел и о действиях над ними – трудный и далеко не элементарный раздел математики. Правда, в таком общем понимании этот раздел принято скорее называть «высшая арифметика» или, чаще, «теория чисел», чтобы своеобразно противопоставить его школьной, начальной арифметике. Но эти названия вовсе не должны заменять суть дела. А она состоит в том, что и школьная арифметика, и теория чисел относятся к одной и той же области знаний.
В качестве отправного пункта мы будем рассматривать так называемую основную теорему арифметики. Это несколько заумное название не должно отпугивать: все эту теорему хорошо знают и при арифметических вычислениях часто ею пользуются (например, при нахождении общего знаменателя дробей), не сознавая, что это – глубокая теорема, требующая, в действительности, внимательного и подробного доказательства и изучения. Этим мы с Вами понемногу и займемся.
Простые и составные числа
Вы, конечно, хорошо знаете, что среди натуральных чисел есть простые и составные. Дадим конкретные определения этим понятиям, дабы в дальнейшем придать четкости нашим рассуждениям.
Определение 1. Простым числом называется натуральное число, имеющее ровно два различных натуральных делителя: единицу и самого себя.
Определение 2. Составное число – это натуральное число, большее 1, которое не является простым. Каждое составное число является произведением двух натуральных чисел, больших 1.
Таким образом, все натуральные числа, большие единицы, разбиваются на простые и составные. Заметим, что с точки зрения данных определений единица не является ни простым, ни составным числом.
Упражнение. Докажите, что все простые числа (за исключением двойки) нечетны.
Делимость – одно из основных понятий арифметики и теории чисел, связанное с операцией деления. С точки зрения теории множеств, делимость является отношением, определённым на множестве целых чисел (подробнее об отношениях в теории множеств мы с Вами узнаем несколько позже).
Простые числа являются своего рода «кирпичиками», из которых можно построить все остальные числа. В каком же смысле? Рассмотрим число 420. Оно, без сомнения, составное. Его можно разложить на множители, например, так: 420 = 42 ∙ 10. Каждое из чисел 42 и 10 также составное: 42 = 6 ∙ 7, а 10 = 2 ∙ 5. Поскольку 6 = 2 ∙ 3, то можем записать такую цепочку равенств: 420 = 42 ∙ 10 = 6 ∙ 7 ∙ 2 ∙ 5 = 2 ∙ 3 ∙ 7 ∙ 2 ∙ 5 = 2 ∙ 2 ∙ 
3 ∙ 5 ∙ 7. Мы получили разложение нашего числа на простые сомножители.
Вряд ли у кого-то вызывает сомнения, что, действуя таким же образом, можно представить в виде произведения простых чисел любое натуральное число (кроме 1) – надо раскладывать получающиеся сомножители в произведение меньших, пока это удается. А что, если попробовать разложить число 420 на множители по-другому? Например, начав так: 420 = 15 ∙ 28. Вы, конечно, догадываетесь, что в результате получится то же самое разложение (если в конце простые сомножители расположить в порядке возрастания). Именно этот интуитивно очевидный, но совсем не просто доказываемый факт, и носит громкое название основной теоремы арифметики.
Основная теорема арифметики
Основная теорема арифметики:
Каждое натуральное число n, за исключением единицы, раскладывается в произведение простых сомножителей, причем единственным образом с точностью до порядка следования сомножителей:
,
где p 1, …, pk – простые числа.
Замечание. На самом деле, единицу можно считать произведением нулевого количества простых чисел, «пустым произведением».
Следствие. Каждое натуральное число n единственным образом представимо в виде
,
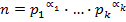где p 1 < p 2 < … < pk – простые числа, а α1, …, α k – некоторые натуральные числа.
Такое представление числа n называется его каноническим разложением на простые сомножители.
Доказательство основной теоремы арифметики заслуживает отдельного разговора. Однако пока что мы с Вами примем эту теорему без доказательства.
Теперь же, зная, что разложение любого натурального числа на произведение простых сомножителей единственно, мы можем рассмотреть следующую схему получения такого разложения.
Возьмем, к примеру, число 882. Перебираем последовательно простые числа, начиная с двойки. 882 делится на 2. Следовательно, в разложении числа 882 на произведение простых сомножителей будет двойка как минимум в первой степени. Разделим 882 на 2. Получим 441. Число 441 на 2 не делится, но делится на 3. Тогда мы можем утверждать, что в разложении числа 882 должна присутствовать и тройка (снова же – как минимум в первой степени). Разделив 441 на 3, получаем 147. Продолжаем этот процесс, пока не получим единицу. Кратко это записывается в таком виде:
Исходя из схемы, теперь несложно записать искомое разложение (записываем сомножители в порядке возрастания, сверху вниз): 882 = 2 ∙ 32 ∙ 72.
Рассмотрим несколько примеров составления такого разложения.
Примеры.
270 = 2 ∙ 33 ∙ 5 | 415 = 5 ∙ 83 | 549 = 32 ∙ 61 | 693 = 32 ∙ 7 ∙ 11 |
Следует отдельно обратить внимание на то, что свойства делимости практически полностью определяются разложением числа на простые множители. Таким образом, для того, чтобы сделать вывод о делимости одного числа на другое, следует разложить их на простые множители и убедиться, что степени множителей делителя не превышают степеней соответствующих множителей делимого.
К примеру, число 1323 = 33 ∙ 72 будет делиться нацело на 63 = 32 ∙ 7 (поскольку 2 < 3 и 1 < 2), но не будет делиться на 567 = 34 ∙ 7 (поскольку 4 > 3).
Задачи.
1. Делится ли 29 ∙ 3 на 2?
Решение. Да, так как 2 входит в разложение этого числа на простые множители.
2. Делится ли 29 ∙ 3 на 5?
Решение. Нет, потому что в разложении этого числа на простые множители нет простого числа 5.
3. Делится ли 29 ∙ 3 на 8?
Решение. Да, поскольку 8 = 23, а в разложение данного числа на простые множители двойка входит 9 раз (9 > 3).
4. Делится ли 29 ∙ 3 на 9?
Решение. Нет, так как в разложение данного числа на простые множители тройка входит лишь один раз, а в разложение числа 9 – дважды.
5. Делится ли 29 ∙ 3 на 6?
Решение. Да, потому что 6 = 2 ∙ 3, а 2 и 3 входят в разложение данного числа на простые.
6. Верно ли, что если натуральное число делится на 4 и на 3, то оно делится на 12?
Решение. Да. В разложение на простые множители числа, делящегося на 4, двойка входит по крайней мере 2 раза. Поскольку число делится и на 3, то в его разложение входит и тройка. Поэтому оно делится на 12.
7. Верно ли, что если натуральное число делится на 4 и на 6, то оно делится на 24?
Решение. Нет. Например, число 12. Дело в том, что если число делится на 4, то в его разложение на простые множители по крайней мере дважды входит число 2; из делимости числа на 6 следует, что в его разложении есть 2 и 3. Таким образом, заведомо в это разложение входят две (не три!) двойки и одна тройка, и можно утверждать лишь то, что число делится на 12.
8. Число a не делится на 3. Может ли на 3 делиться число 2 a?
Решение. Нет, поскольку тройка не входит в разложение на простые множители числа a, а значит, не входит и в разложение числа 2 a.
9. Число a – четно. Верно ли, что 3 a делится на 6?
Решение. Да, так как 2 и 3 входят в разложение числа 3 a на простые множители.
10. Число 5 a делится на 3. Верно ли, что a делится на 3?
Решение. Да, потому что в разложение числа 5 a на простые множители тройка входит, а в разложение простого числа 5 – нет.
11. Число 15 a делится на 6. Верно ли, что a делится на 6?
Решение. Нет. Например, a = 2. Дело в том, что тройка, входящая в разложение числа 6, входит и в разложение числа 15. Поэтому можно утверждать лишь то, что в разложении числа a обязательно есть двойка.
Определение 3. Два числа называются взаимно простыми, если у них нет общих делителей, отличных от единицы.
Упражнение. Докажите, что любые два разных простых числа всегда являются взаимно простыми.
Понятие делимости
Разобравшись с основной теоремой арифметики и примерами ее применения, теперь мы сделаем небольшое отступление к самому началу нашей темы. Мы с Вами введем вполне конкретные определения для тех понятий, которыми уже начали пользоваться давным-давно, попробуем их формализовать, а также обратим внимание на некоторые немаловажные свойства.
Определение 1. Пусть a и b – целые числа, причем b ≠ 0. Тогда число a делится нацело (чаще говорят просто «делится») на число b (или, что то же самое, число b является делителем числа a), если существует такое целое число q, что a = q ∙ b.
Обозначение. a 
b.
На самом деле, введенное нами определение содержит в себе одну из серьезных теорем теории чисел. Однако мы с Вами не будем вдаваться в дебри теории, а позволим себе в этом и некоторых следующих определениях небольшие неточности, наподобие этой, о которых зачастую многие даже не вспоминают.
Замечание. Нередко вместо фразы «число a делится на число b» говорят «число a кратно числу b» либо же «число b делит число a». Все эти выражения имеют один и тот же смысл. Мы будем пользоваться каждым из них.
Подчеркнем, что запись a b означает не какое-то действие, которое надлежит произвести над числами a и b, а некоторое утверждение, касающееся этих чисел. В зависимости от того, каковы числа a и b, утверждение a b может быть верным либо неверным. Так, например, 4 2 верно, а 4 3 – неверно.
Заметим, что введенное отношение делимости между числами a и b обладает довольно интересными свойствами:
1. Рефлексивность (возвратность).
Любое число a делится само на себя – a a.
2. Транзитивность (переходность).
Если a b и b c, то a c.
Доказательство. Поскольку a b, то, по определению, существует некоторое целое число q такое, что a = q ∙ b. Аналогично так как b c, то существует целое число p, причем b = p ∙ c. Тогда a = q ∙ b = q ∙ (p ∙ c) = (q ∙ p) ∙ c. Поскольку q ∙ p, очевидно, целое, то a c.
3. Антисимметричность.
Если a b и b a, то либо a = b, либо a = – b.
Упражнение. Докажите свойства 1 и 3.
Определение 2. Если a и b – два целых числа, отличных от нуля, и если число k таково, что a k и b k, то k называется общим делителем чисел a и b.
Заметим, что произвольные два числа всегда обладают общими делителями. Таковыми являются числа 1 и –1. Дабы избежать в дальнейшем лишних уточнений, далее мы будем считать, что все рассматриваемые числа являются натуральными (а не целыми, как мы предполагали в первых двух определениях), если не указано другое.
