Структурные средние величины

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены,в основном, модой и медианой.

где:

§ — значение моды

§ — нижняя граница модального интервала

§ — величина интервала

§ — частота модального интервала

§ — частота интервала, предшествующего модальному

§ — частота интервала, следующего за модальным

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

М_е = (n_{(число признаков в совокупности)} + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

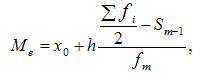
где:

§ — искомая медиана

§ — нижняя граница интервала, который содержит медиану

§ — величина интервала

§ — сумма частот или число членов ряда

§ - сумма накопленных частот интервалов, предшествующих медианному

§ — частота медианного интервала

Пример. Найти моду и медиану.

Возрастные группы	Число студентов	Сумма накопленных частот ΣS
До 20 лет
20 — 25
25 — 30
30 — 35
35 — 40
40 — 45
45 лет и более
Итого

Решение:
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).

Рассчитаем величину моды:

Это значит что модальный возраст студентов равен 27 годам.

Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σf_i/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:

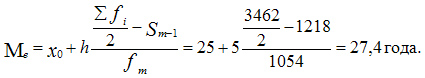
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.