· Щелкните в свободном месте рабочего документа и нажмите комбинацию клавиш [Shift]+7 (или щелкните на соответствующей кнопке палитры).
· Появится знак интеграла с пустыми полями для подинтегрального выражения, пределов интегрирования и переменной интегрирования.
· Заполните пустые поля. Пределы интегрирования должны быть вещественными.
· Кроме переменной интегрирования все переменные в подинтегральном выражении должны быть определены ранее в другом месте рабочего документа.
· Переменная интегрирования должна быть простой переменной без индекса.
· Если переменная интегрирования является размерной величиной, верхний и нижний пределы интегрирования должны иметь ту же самую размерность.
Если подинтегральное выражение имеет особенности, разрывы, численное решение, найденное MathСAD, может быть неточно.
Можно использовать интеграл совместно с дискретным аргументом, чтобы получить результаты для многих значений параметра.
Пример 2.4. Использование интеграла совместно с дискретнымаргументом:
 |
Чтобы вычислитьдвойной интеграл, необходимо:
· щелкнуть дважды мышью по символу интеграла на соответствующей палитре символов
· ввести подынтегральное выражение, пределы и переменные интегрирования для каждого интеграла
· нажать символ =
 |
Пример 2.5. Отыскание центра масс треугольника, задаваемого неравенствами
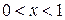 и
и  , плотность которого пропорциональна расстоянию от начала координат:
, плотность которого пропорциональна расстоянию от начала координат:
Неопределенный интеграл. Для вычисления неопределенного интеграла можно использовать палитру инструментов Calculus (Матанализ), а можно интегрировать выражение, не используя оператор вычисления неопределенного интеграла. Для этого используется комбинация клавиш [Ctrl]+I (или необходимо щелкнуть мышью на соответствующей кнопке палитры интегралов и производных). Чтобы вставить оператор неопределенного интеграла и поля ввода его параметров, нужно
1. заполнить поле ввода для подинтегрального выражения;
2. поместить переменную интегрирования в поле ввода, следующее за " d ", это может быть имя любой переменной;
3. охватить маркером ввода весь интеграл и нажать комбинацию клавиш [Shift]+F9
Команда символьного меню Variable-Integrate (Интегрировать по переменной) интегрирует выражение по выделенной переменной. Если не выделить переменную, команда меню будет записана серым. MathСAD не может интегрировать, не зная переменной интегрирования. Если символьный процессор не может найти неопределенный интеграл, он возвращает интеграл неизмененным. Следует помнить, что результат интегрирования неоднозначен. Если  – интеграл данной функции, то для любой константы С интегралом будет также
– интеграл данной функции, то для любой константы С интегралом будет также  . Ответ, получаемый MathСAD, может отличаться на константу от ответа, который можно найти в таблицах. Если продифференцировать функцию и затем проинтегрировать полученный результат, не обязательно получится в качестве ответа исходная функция.
. Ответ, получаемый MathСAD, может отличаться на константу от ответа, который можно найти в таблицах. Если продифференцировать функцию и затем проинтегрировать полученный результат, не обязательно получится в качестве ответа исходная функция.
Пример 2.6. Интегрирование выражений:
 |
Символьный знак равенствапозволяет MathСad выйти за рамки численного вычисления выражений. Для его использования необходимо
1. Убедиться, что режим Automatic Calculations (Автоматический режим)из меню Math (Математика) включен, в противном случае его можно включить из меню.
2. Ввести выражение, которое надо упростить.
3. Нажать комбинацию клавиш [Ctrl]-. (точка), MathСAD отобразит символ стрелки. Если щелкнуть мышью вне выражения, MathСAD отобразит упрощенную версию первоначального выражения. Если выражение не может быть упрощено, MathСAD просто повторяет его справа от стрелки.
 |
Пример 2.7.
Замечание 2.1. Символьный знак равенства является оператором, подобным любому оператору MathСAD. Применяется только ко всему выражению. Пример использования символьного знака равенства.
Встроенные функции. Это основной набор функций, которые поставляются вместе с пакетом MathСAD. Чтобы просмотреть список всех встроенных функций, выберите команду Function (Функция) из меню Insert (Вставка) или щелкните на f(x) на панели инструментов или нажмите комбинацию клавиш [Ctrl]+F. Имена встроенных функций чувствительны к регистру. Они должны быть напечатаны с использованием прописных или строчных букв (рис.2.2).
Чтобы задать встроенную функцию в рабочем документе, нужно:
1. щелкнуть мышью в свободном месте рабочего документа
2. дважды щелкнуть по имени функции, которую необходимо вставить (или пометить ее и щелкнуть по кнопке " OK " или набрать с клавиатуры).
Левый список диалогового окна показывает все встроенные функции наряду с их аргументами. Внизу описание выбранной функции.

Рис. 2.2. Встроенные функции
Порядок выполнения работы
Студенту рекомендуется изучить внимательно теоретический материал, проделать все примеры, в нем встречающиеся, и после этого приступать к выполнению своего варианта задания.
Содержание отчета
1. Краткий обзор по теоретической части.
2. Ответы на контрольные вопросы.
3. Файл MathCAD с выполненными заданиями своего варианта.
Контрольные вопросы
1. Какие операторы используются в Mathcad? Как их можно вводить?
2. Операторы вычисления сумм и произведений: способы задания, примеры.
3. Оператор производной: способ задания, дифференцирование в точке, символьное дифференцирование, примеры.
4. Определенный интеграл: способ задания, переменные пределы интегрирования. Двойной и тройной интегралы.
5. Неопределенный интеграл: способ задания, примеры.
6. Символьный знак равенства, способы его задания, примеры.
7. Встроенные функции.
Варианты заданий
Вариант 1
1. Вычислить  .
.
2. Вычислить пределы: а)  ; б)
; б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б) 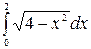 .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 2
1. Вычислить 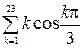 .
.
2. Вычислить пределы а)  ; б)
; б)  .
.
3. Продифференцировать функцию 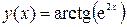 символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 3
1. Вычислить  .
.
2. Вычислить пределы а)  ; б)
; б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 4
1. Вычислить  .
.
2. Вычислить пределы а)  ; б)
; б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 5
1. Вычислить  .
.
2. Вычислить пределы а) 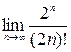 ; б)
; б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а) 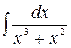 ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 6
1. Вычислить  .
.
2. Вычислить пределы а)  ; б)
; б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 7
1. Вычислить  .
.
2. Вычислить пределы: а)  ; б)
; б) 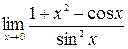 .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 8
1. Вычислить  .
.
2. Вычислить пределы: а)  ; б)
; б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б) 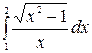 .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Вариант 9
1. Вычислить 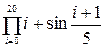 .
.
2. Вычислить пределы а)  ; б)
; б)  .
.
3. Продифференцировать функцию 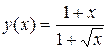 символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы
а)  ; б)
; б)  .
.
Вариант 10
1. Вычислить  .
.
2. Вычислить пределы: а)  , б)
, б)  .
.
3. Продифференцировать функцию  символьно и в точке
символьно и в точке  .
.
4. Вычислить частные производные первого и второго порядка для функции  .
.
5. Вычислить интегралы: а)  ; б)
; б)  .
.
6. Вычислить двойной и тройной интегралы:
а)  ; б)
; б)  .
.
Л а б о р а т о р н а я р а б о т а № 3
Графические возможности пакета инженерных расчетов MathCAD.
Цель работы: Изучение графических возможностей символьного пакета MathCAD. Приобретение навыков построения графиков функции и поверхностей. Знакомство с возможностями анимации.
Используемые программные средства: Пакет MathCAD.
Теоретические сведения
В пакете MathCAD встроено несколько различных типов графиков, которые можно разделить на двумерные (или графики на плоскости) и трехмерные (графики в пространстве) В свою очередь двумерные графики делятся на:
- XY (декартовый) график (XY Plot);
- полярный график (Polar Plot).
Среди трехмерных выделяют
- график трехмерной поверхности (Surface Plot);
- график линий уровня (Contour Plot);
- трехмерная гистограмма (3D Bar Plot);
- трехмерное множество точек (3D Scatter Plot);
- векторное поле (Vector Field Plot).
Деление графиков на типы несколько условно, так как управляя установками многочисленных параметров, можно создавать комбинации типов графиков, а также новые типы (например, двумерная гистограмма распределения является разновидностью простого XY -графика).
Все графики создаются аналогичным способом, с помощью панели инструментов Graph (График), различия обусловлены отображаемыми данными.
Некорректное определение данных приводит, вместо построения графика, к выдаче сообщения об ошибке.
Построение двумерного графика. К двумерным графикам относят графики в декартовой и полярной системах координат. Созданный однажды график одного типа нельзя переделать в график другого типа (в отличие от трехмерных графиков). Для построения XY -графика необходимы два ряда данных, откладываемых по осям ОХ и ОУ.
Для построения нужно:
· щелкнуть мышью в свободном месте рабочего документа;
· нажать комбинацию клавиш [shift] + 2, или щелкнуть мышью по палитре графических операторов, или выбрать пункт X - Y Plot из меню Insert (Вставка).
Появляется шаблон декартова графика с полями ввода для выражений, отображаемых по осям графика.
XY-график двух векторов.
Самый простой и наглядный способ получить декартов график – это сформировать два вектора данных, которые будут отложены вдоль осей ОХ и ОУ. Последовательность построения графика двух векторов х и у показана на рис. 3.1. В этом случае в шаблоны возле осей вводятся просто имена векторов. Также допускается откладывать по осям элементы векторов, т. е. вводить в шаблоны возле осей имена  и
и  соответственно. В результате получается график, на котором отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Образованная ими ломаная называется рядом данных, или кривой (trace).
соответственно. В результате получается график, на котором отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Образованная ими ломаная называется рядом данных, или кривой (trace).
Пример 3.1. Построение двумерного графика
 |
XY-график функции.
 |
График любой скалярной функции
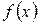 можно построить двумя способами. Первый заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора (рис. 3.2).
можно построить двумя способами. Первый заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора (рис. 3.2).
Второй способ, называемый быстрым построением графика, заключается во введении функции в один из шаблонов (например, у оси ординат), а имени аргумента – в шаблон у другой оси абсцисс (рис.3.3 – 3.5). В шаблоны слева и справа от аргумента необходимо ввести границы диапазона изменения значений аргумента. Если такой диапазон не задан, по умолчанию график будет построен в диапазоне значений аргумента от –10 до 10.
 |
Построение графиков в полярных координатах. Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) и вставить в появившиеся шаблоны имена переменных и функций, которые будут нарисованы в полярной системе координат: угол (нижний шаблон) и радиус-вектор (левый шаблон). Аналогично построению графика в декартовых координатах по осям могут быть отложены два вектора, элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции (рис.3.6, 3.7).
|

График функции в полярных координатах можно построить также с помощью преобразований полярных координат в декартовые.
На рис. 3.8 показан пример построения графика кардиоиды в полярных координатах, уравнение которого задано в виде  . Уравнения для
. Уравнения для  и
и 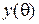 – обычное преобразование полярных координат в прямоугольные (декартовые).
– обычное преобразование полярных координат в прямоугольные (декартовые).

Рис. 3.8
Размещение нескольких графиков на чертеже. График может содержать несколько выражений по оси ординат в зависимости от одного выражения по оси абсцисс или несколько значений по оси ординат, согласованных с соответствующими выражениями по оси абсцисс. Чтобы представить графически несколько выражений по оси ординат относительно одного выражения по оси абсцисс, необходимо ввести первое выражение для оси ординат, а затем нажать клавишу [, ] (запятая). Непосредственно под первым выражением появится пустое поле (шаблон). В появившемся месте ввода записывается имя второй функции, сопровождаемое другой запятой и т.д. Все выражения должны использовать одну и ту же переменную (рис.3.9, 3.10).
|


Чтобы построить несколько независимых кривых на одном чертеже, введите два или более выражения, отделяемых запятыми на оси абсцисс, и то же самое число выражений на оси ординат (рис. 3.11). MathCAD согласует выражения попарно: первое выражение оси абсцисс с первым выражением оси ординат, второе со вторым и т.д.
 |
Можно построить до 16 функций на оси ординат в зависимости от одного аргумента на оси абсцисс. Если для каждой кривой используется свой аргумент, то можно отобразить только до 10 графиков.
Все графики на чертеже совместно используют одни границы на осях. Для каждой оси все выражения и границы должны иметь совместимые размерности.
Форматирование двумерных графиков. Изменение размеров графика. Чтобы изменить размеры графика, необходимо:
1. Заключить его в выделяющий прямоугольник с помощью щелчка мыши.
2. Переместить указатель мыши к левому нижнему краю выделяющего прямоугольника. Указатель превратится в двойную стрелку.
3. Переместить указатель при нажатой кнопке мыши, растягивая графическую область в желаемом направлении.
4. По достижении желаемого размера отпустить кнопку мыши.
Для отмены выделения щелкните мышью вне графической области.
При двойном щелчке мышью в области графика (либо выборе в контекстном меню команды Format) открывается окно форматирования графика с четырьмя вкладками.
1) На вкладке Trace (Трассировки) предоставляется возможность задать следующие параметры линий:
· Line (Линия) – стиль линии.
- solid – сплошная;
- dot – мелкий пунктир;
- dadot – штрих-пунктир;
- dash – крупный пунктир.
· Color (Цвет) цвет линии и точек данных,
· Weight (Толщина) – толщина линии и точек данных,
· Type (Тип) – тип представления ряда данных:
- line – линия;
- point – точка;
- bar – столбик гистограммы;
- solidbar – закрашенный столбик;
- step – ступенька;
- stem – палочка с кружочком;
- draw – рисованная линия;
- error – позволяет отложить на графике вычисленную ошибку
2) Сохранение установок по умолчанию.
На вкладке Defaults (По умолчанию) диалога Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) находятся два элемента управления:
- кнопка Change to Defaults (Вернуть установки по умолчанию) позволяет изменить все установки выделенного графика на установки по умолчанию, принятые для текущего документа;
- флажок проверки Use for Defaults (Использовать для установок по умолчанию) фиксирует установками по умолчанию для данного документа установки выбранного графика.
3) Создание заголовка графика с помощью вкладки Labels.
Чтобы создать заголовок графика, необходимо:
1. Дважды щелкнуть мышью в области графика.
2. В диалоге Formatting Currently Selected X-Y Plot (Форматирование выбранного графика) перейти на вкладку Labels (Метки).
3. В поле Title (Заголовок) ввести текст заголовка.
4. Установить флажок проверки Show Title (Показать заголовок).
5. Выбрать переключатель Above (Сверху) или Below (Снизу), чтобы заголовок появился сверху или снизу графика.
6. Нажать кнопку ОК.
4) Форматирование осей графиков с помощью вкладки X-Y Axes.
Возможности форматирования координатных осей графиков включают в себя управление их внешним видом, диапазоном, шкалой, нумерацией и отображением некоторых значений на осях при помощи маркеров.
Изменение диапазона осей.Когда график создается впервые, MathCAD выбирает представленный диапазон для обеих координатных осей автоматически. Чтобы изменить этот диапазон, нужно:
1. Перейти к редактированию графика, щелкнув в его пределах мышью. График будет выделен, а вблизи каждой из осей появятся два поля с числами, обозначающими границы диапазона.
2. При щелчке мышью в области одного из полей, чтобы редактировать соответствующую границу оси (например, верхнего предела оси х).
3. Пользуясь клавишами управления курсором и клавишами BackSpace или Del, удалите содержимое поля.
4. Введите новое значение диапазона.
5. Щелкните за пределами поля, и график будет автоматически перерисован в новых пределах.
Предусмотрена еще удобная возможность просмотра графика в увеличенном масштабе. Для этого необходимо
1. Щелкнуть правой кнопкой мыши и в контекстном меню выбрать команду Zoom (Масштаб) – откроется диалоговое окно X-Y Zoom (Масштаб по осям Х и У).
2. Обвести указателем мыши при нажатой левой кнопке мыши ту область графика, которую необходимо увеличить – эта область окажется обведенной пунктирной линией.
3. В открытом окне щелкнуть по кнопке Zoom (Масштабировать) – выделенная область увеличится.
Чтобы вернуться к исходному виду графика, используются кнопки Unzoom (отменить масштабирование) или Full View (Вид полностью). Чтобы закрыть окно, оставив график увеличенным, необходимо нажать клавишу ОК.
Построение графиков поверхностей. Для построения графика поверхности с уравнением  надо определить матрицу значений аппликат точек поверхности, которую необходимо отобразить графически. MathCAD будет использовать номер строки и номер столбца матрицы в качестве координат по осям X и Y. Элементы матрицы будут представлены на графике как высоты выше или ниже плоскости X-Y.
надо определить матрицу значений аппликат точек поверхности, которую необходимо отобразить графически. MathCAD будет использовать номер строки и номер столбца матрицы в качестве координат по осям X и Y. Элементы матрицы будут представлены на графике как высоты выше или ниже плоскости X-Y.
Для построения графика поверхности нужно нажать комбинацию клавиш [Сtrl] + 2 или щелкнуть мышью на графической палитре инструментов, или из меню Вставка (Insert) выберите команду Grafics (Surface plot). MathCAD покажет рамку с одним полем ввода, в которое вводится имя матрицы. Остаётся установить указатель мыши вне графического блока и щёлкнуть левой кнопкой. По умолчанию ориентация поверхности такова, что первая строка матрицы простирается из дальнего левого угла сетки, а первый столбец из дальнего левого угла по направлению к наблюдателю. MathCAD рисует линии, чтобы соединить точки на графике. Эти линии определяют поверхность. Типичный график поверхности показывает значения функции двух переменных. Чтобы создать такой график, необходимо сначала образовать матрицу, содержащую значения  этой функции, а затем построить поверхностный график этой матрицы (рис. 3.12).
этой функции, а затем построить поверхностный график этой матрицы (рис. 3.12).
 |
Быстрое построение графика (рис. 3.13). Для быстрого построения графика необходимо:
1. Задать функцию двух переменных.
2. Установив курсор в то место, де нужно построить график, отрыть панель (График) и щелкнуть по кнопке (График поверхности). На экране появится шаблон графика.
3. В месте ввода ввести имя функции без аргументов.
Кроме графиков поверхности, MathCAD также может строить карты линий уровня (рис.3.14), трехмерные гистограммы (рис.3.15), точечные графики (рис.3.16) и графики векторных полей (рис. 3.17).
Пример 3.1.


Форматирование графика поверхности. Форматирование трехмерных графиков выполняется с помощью диалогового окна 3-D Plot Format (Форматирование 3-D графика), которое вызывается двойным щелчком мыши в области графика. Параметры трехмерных графиков всех типов устанавливаются посредством этого диалогового окна. В диалоге 3-D Plot Format (Форматирование 3-D графика) доступно большое количество параметров, изменение которых способно очень сильно повлиять на внешний вид графика. Они сгруппированы по принципу действия на нескольких вкладках.
Изменение типа графика. Чтобы поменять тип уже имеющегося графика (например, построить вместо поверхности график линий уровня и т. д.), соответствующий переключатель в нижней части вкладки General (Общие) установите в необходимое положение. После нажатия кнопки ОК график будет перерисован.
Вращение графика. Самый простой способ изменения ориентации системы координат с графиком в трехмерном пространстве – это перетаскивание ее указателем мыши. Попробуйте перемещать при нажатой левой кнопке мыши указатель в пределах графика, и вы увидите, как поворачивается график. Другой способ изменения ориентации графика – с помощью полей Rotation (Вращение), Tilt (Наклон) и Twist (Поворот) на вкладке General (Общие), которые в совокупности определяют соответствующие углы (в градусах) и тем самым задают направление всех трех осей координат в пространстве. Оперирование мышью с нажатой клавишей Shift позволяет после отпускания левой кнопки наблюдать анимированную картину вращения поверхности в любом заданном направлении. Для остановки вращения надо щёлкнуть левой кнопкой мыши.
Масштабирование графика. В поле Zoom (Масштаб) вкладки General (Общие) можно задать числовое значение масштаба.
Форматирование осей. Вкладка Axes (Оси) содержит три вложенных вкладки, в которых задаются параметры для каждой из трех координатных осей. В частности, можно включить или отключить показ линий сетки, нумерации и задать диапазон по каждой из осей. Смысл этих операций сходен с аналогичными операциями для двумерных графиков. При помощи еще одной вкладки – Backplanes (Плоскости заднего плана) задается показ проекций координатной сетки на три скрытые плоскости трехмерного графика.
Стиль заливки и линий. С помощью вкладки Appearance (Появление) для контурного и поверхностного графиков можно выбрать стиль заливки линий графика поверхности. При выборе переключателя Fill Surface (Заливка поверхности) из группы Fill Options (Опции заливки) вы получаете доступ к опциям цвета (в группе Color Options). Если выбрать переключатель Solid Color (Один цвет), то получится однотонная заливка поверхности. Если установить переключатель Color-map (Цветовая схема), то поверхность или контурный график будут залиты разными цветами и оттенками, причем выбрать цветовую схему можно на вкладке Advanced (Дополнительно).
Спецэффекты. Во вкладке Advanced (Дополнительно) имеется доступ к управлению несколькими специальными эффектами оформления графиков, благодаря которым они выглядят более красиво:
- Shininess (Сияние) – имеется возможность регулировать сияние в пределах от 0 до 128;
- Fog (Туман) - эффект тумана;
- Transparency (Прозрачность) – задается процент прозрачности графика;
- Perspective (Перспектива) – показ перспективы с определением видимости расстояния.
Еще один спецэффект подсветки графика задается на вкладке Lighting (Подсветка), причем имеются как встроенные схемы подсветки, так и возможность задавать ее цвет и направление самому пользователю.
Порядок выполнения работы
Студенту рекомендуется изучить внимательно теоретический материал, проделать все примеры, в нем встречающиеся, и после этого приступать к выполнению своего варианта задания.
Содержание отчета
Отчет должен содержать ответы на контрольные вопросы, результат решения соответствующего варианта.
Контрольные вопросы
1. Двумерные графики в Mathcad: построение, изменение размеров.
2. Форматирование двумерных графиков.
3. Построение нескольких графиков на одном чертеже. Имена кривых и отображаемые переменные.
4. Построение поверхностей.
5. Форматирование поверхностей.
Варианты заданий
Вариант 1
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций 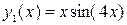
 .
.
3. В полярной системе координат построить график трехлепестковой розы 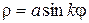 для
для 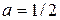 ,
,  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 2
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций 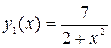 ,
,  .
.
3. В полярной системе координат построить график спирали Архимеда 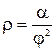 для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 3
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
,  .
.
3. В полярной системе координат построить график улитки Паскаля  для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 4
1. Построить график функции 
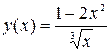 .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
, 
3. В полярной системе координат построить график розы 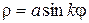 для
для  ,
,  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 5
1. Построить график функции  .
.
2. Построить в одной системе координат при 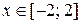 графики функций
графики функций  ,
,  .
.
3. В полярной системе координат построить график спирали Галилея  ,
,  для
для  ,
,  .
.
4. Построить поверхность 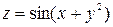 , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 6
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
, 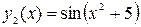 .
.
3. В полярной системе координат построить график строфоиды 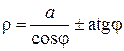 для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 7
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
,  .
.
3. В полярной системе координат построить график розы  для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 8
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
,  .
.
3. В полярной системе координат построить график кардиоиды  для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 9
1. Построить график функции 
2. Построить в одной системе координат графики функций  ,
,  .
.
3. В полярной системе координат построить график логарифмической спирали  для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 10
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
, 
3. В полярной системе координат построить график спирали «жезл» 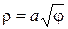 , для
, для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 11
1. Построить график функции  .
.
2. Построить в одной системе координат при  графики функций
графики функций  ,
,  .
.
3. В полярной системе координат построить график гиперболической спирали  для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Вариант 12
1. Построить график функции  .
.
2. Построить в одной системе координат графики функций 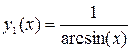 ,
,  .
.
3. В полярной системе координат построить график циссоиды Диоклеса  для
для  .
.
4. Построить поверхность  , окрасить её и выполнить вращение.
, окрасить её и выполнить вращение.
Л а б о р а т о р н а я р а б о т а № 4
Решение обыкновенных дифференциальных уравнений
Цель работы: Изучение вычислительных возможностей пакета MathCAD при решении задачи Коши для некоторых типов обыкновенных дифференциальных уравнений (ОДУ).
Используемые программные средства: пакет MathCAD.
Теоретические сведения
ОДУ  - го порядка имеет вид:
- го порядка имеет вид:
 или
или  ,
,
где 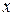 – независимая переменная,
– независимая переменная,  - искомая функция,
- искомая функция,  – ее производные. Задача нахождения решения уравнения, удовлетворяющего начальным условиям
– ее производные. Задача нахождения решения уравнения, удовлетворяющего начальным условиям


называется задачей Коши.
Дифференциальные уравнения первого порядка. ОДУ 1-го порядка имеет вид:
 или
или 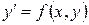 .
.
Задача Коши для этого уравнения: найти такое решение уравнения, которое удовлетворяет начальному условию  .
.
Уравнение с разделяющимися переменными. ОДУ вида:  или
или  называется уравнением с разделяющимися переменными, оно приводится к уравнению с разделенными переменными:
называется уравнением с разделяющимися переменными, оно приводится к уравнению с разделенными переменными:
 ,
,
которое решается почленным интегрированием. 
Пример 4.1. Найти решение уравнения  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  (задача Коши). Изобразите график решения (интегральную кривую, проходящую через точку (0, 1)).
(задача Коши). Изобразите график решения (интегральную кривую, проходящую через точку (0, 1)).
Решение.
1) Разделите в уравнении переменные: 
2) Установите режим автоматических вычислений.
3) Установите режим отображения результатов символьных вычислений по горизонтали, установив метку Horizontally в окне диалога строки Evaluation Style меню Symbolics.
4) Введите начальные условия  :
:
5) Определите подынтегральные функции  и
и  :
: 
 ;
; 
6) Решите уравнение, задающее неявно  как функцию переменной
как функцию переменной  :
:
Given
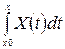 =
= 

Для решения этого уравнения используется символьный процессор MathCAD (аналогично применению вычислительного блока для численного решения нелинейных уравнений).
Здесь Given – ключевое слово.
Логический знак жирного равенства вводится с палитры Booleans. Завершает блок встроенная функция  , после которой следует набрать символьный знак равенства из меню Symbolic (подменю Evaluation).
, после которой следует набрать символьный знак равенства из меню Symbolic (подменю Evaluation).
7) Решение, удовлетворяющее условию  :
:

8) Постройте график найденного решения:
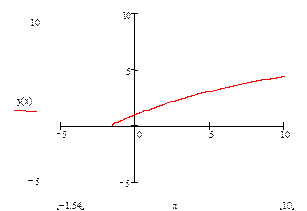 |
Численный метод Рунге-Кутта решения задачи Коши для ОДУ 1-го порядка. Нахождение точного решения задачи Коши для многих типов ОДУ затруднительно, иногда невозможно, поэтому было создано множество приближенных методов. Один из самых популярных – метод Рунге-Кутта четвертого порядка, дающий приближенное решение в виде таблицы значений этого решения в отдельных точках заданного интервала для независимой переменной 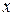 . В пакете MathCAD есть встроенная функция, реализующая этот метод:
. В пакете MathCAD есть встроенная функция, реализующая этот метод:
 ,
,
где  – вектор начальных условий (для ОДУ 1-го порядка – это точка
– вектор начальных условий (для ОДУ 1-го порядка – это точка 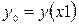 ,
,
 – границы интервала, на котором ищется решение ДУ,
– границы интервала, на котором ищется решение ДУ,
 – число точек (не считая начальной), в которых ищется приближенное решение,
– число точек (не считая начальной), в которых ищется приближенное решение,
 – для системы ОДУ 1-го порядка вектор, состоящий из первых производных неизвестных функций (для ДУ 1-го порядка
– для системы ОДУ 1-го порядка вектор, состоящий из первых производных неизвестных функций (для ДУ 1-го порядка 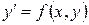 – это
– это 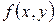 ).
).
Пример 4.2. Решите на отрезке [0, 3] задачу Коши  ,
,  методом Рунге-Кутта с постоянным шагом в
методом Рунге-Кутта с постоянным шагом в  равностоящих точках отрезка
равностоящих точках отрезка  .
.
Решение.
1) Установите режим автоматических вычислений.
2) Присвойте переменной ORIGIN значение, равное 1:

3) Введите начальное условие:

4) Определите правую часть уравнения  :
:
 в
в  равностоящих точках отрезка
равностоящих точках отрезка  .
.
5) Вычислите решение




6) Постройте на одном графике найденные решения:
 |
Дифференциальные уравнения 2-го порядка. ОДУ 2-го порядка имеет вид:
 или
или  .
.
Задача Коши для этого уравнения: найти такое решение, которое удовлетворяет начальным условиям 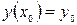 ,
,  .
.
Решение ДУ 2-го порядка методом Рунге - Кутта. С помощью замены переменных  вместо одного ДУ 2-го порядка
вместо одного ДУ 2-го порядка  получим систему двух ДУ 1-го порядка:
получим систему двух ДУ 1-го порядка:

с вектором начальных условий
 .
.
Дальше применяем метод Рунге-Кутта с помощью встроенной функции  , где
, где
 .
.
Пример 4.3. Решите задачу Коши методом Рунге-Кутта и постройте график приближенного решения ДУ  ,
,  ,
,  , по 60 точкам отрезка
, по 60 точкам отрезка  .
.
С помощью замены 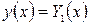 ,
,  вместо заданного ДУ получим систему ДУ
вместо заданного ДУ получим систему ДУ
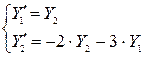
с вектором начальных условий  .
.
Решение.
1) 
2) 
3) 
4) 
 – решение в форме матрицы, I-й столбец которой состоит из значений
– решение в форме матрицы, I-й столбец которой состоит из значений 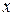 , II-й из значений
, II-й из значений






