Подібно до безперервних систем лінійна імпульсна система буде стійкою, якщо всі корені характеристичного рівняння замкнутої системи будуть лівими, тобто знаходитись у лівій півплощині комплексної площини s. Межею стійкості є уявна вісь, рівняння якої має вигляд s=jw (рис. 8.9, а). Оскільки під час дослідження імпульсних систем застосовуються z-перетворення, визначимо межу стійкості на площині z:
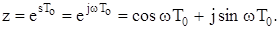
Це рівняння кола одиничного радіуса, яке і є межею стійкості (рис. 8.9, б). Зона стійкості знаходиться в середині цього кола.
 |
Отже, стійкість імпульсної системи можна досліджувати за коренями характеристичного рівняння замкнутої системи D(z)=0: імпульсна система стійка, якщо модулі всіх коренів характеристичного рівняння замкнутої системи менші за одиницю. Якщо модуль хоча б одного кореня перевищує одиницю, то система нестійка; при |z|=1 система знаходиться на межі стійкості.
Для дослідження стійкості імпульсних систем використовують критерії стійкості, які дозволяють оцінити стійкість за коефіцієнтами характеристичного рівняння або за частотними характеристиками.
Алгебраїчні критерії стійкості. Ці критерії (критерії Гурвіца, Рауса, Льєнара-Шипара) було розроблено для дослідження стійкості безперервних систем за коефіцієнтами характеристичного рівняння, яке подано у вигляді поліному. Безпосередньо застосувати їх для дослідження імпульсних систем неможливо, оскільки характеристичне рівняння імпульсної системи у вигляді:
(8.52)
не є поліномом, а для характеристичного рівняння у вигляді:
(8.53)
умовою стійкості є розміщення усіх коренів усередині кола одиничного радіуса у площині коренів z, а не в лівій півплощині.
Тому перед застосуванням алгебраїчних критеріїв стійкості виконують білінійне w-перетворення (8.45), внаслідок чого отримують рівняння у вигляді поліному:
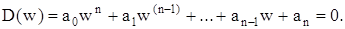(8.54)
Зоною стійкості для його коренів є ліва півплощина коренів w (рис. 8.9,в). і умова стійкості для цього рівняння збігається з умовою стійкості для безперервних систем.
Наприклад, для використання критерію Гурвіца необхідно визначити передавальну функцію замкнутої системи Wз(z)=Q(z)/D(z) і записати характеристичне рівняння D(z)=0. Потім виконати підстановку (8.45) і навести отриманий вираз D(w)=0 до загального знаменника. Чисельник цього виразу, записаний у вигляді поліному
(8.55)
є новим характеристичним рівнянням, за коефіцієнтами якого досліджують стійкість системи.
Згідно з критерієм Гурвіца для стійкості імпульсної системи необхідно і достатньо, щоб при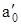 
> 0 визначник Гурвіца і всі його діагональні мінори були додатними.
Приклад 8.8 Визначити за критерієм Гурвіца стійкість системи, характеристичне рівняння якої має вигляд: 25z3 – 5z2 – 10z – 1 = 0.
Виконуємо w-перетворення:
Перетворене характеристичне рівняння має вигляд:
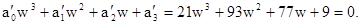
Усі коефіцієнти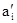 
цього рівняння більше нуля, крім того діагональний мінор другого порядку 
, тому дана система стійка.
Зазначимо, що імпульсні системи другого і першого порядків на відміну від безперервних систем такого самого порядку, можуть бути нестійкими при додатних коефіцієнтах характеристичного рівняння (8.53). Це пояснюється тим, що фіксатор, який входить до складу імпульсної системи, вносить додаткове відставання за фазою.
Частотні критерії стійкості. Для дослідження стійкості імпульсних систем застосовують також частотні критерії стійкості, подібні до критеріїв Михайлова і Найквіста для безперервних систем.
Аналог критерію Михайлова. Під час дослідження стійкості за критерієм Михайлова використовують характеристичне рівняння замкнутої системи (8.53), в якому виконують підстановку 
. Тоді рівняння набуває вигляду:
(8.56)
де
Змінюючи частоту 
від 0 до p, за формулою (8.56) на комплексній площині будуємо криву – аналог годографа вектора Михайлова. За виглядом цього годографа робимо висновок про стійкість системи:
Імпульсна система автоматичного керування стійка, якщо годограф вектора 
при змінюванні частоти від 0 до p починається на додатній дійсній півосі та обходить у додатному напрямку (проти ходу стрілки годинника) послідовно 2n квадрантів, ніде не перетворюючись на нуль; n – порядок характеристичного рівняння.
На відміну від безперервних систем годограф не прямує до нескінченності, а закінчується на дійсній осі, крім того, годограф проходить удвічі більше квадрантів. Якщо годограф проходить через початок координат, то система знаходиться на межі стійкості.
На рис. 8.10 наведені годографи вектора для стійкої (крива 1) і нестійкої (крива 2) систем другого порядку.
Аналог критерію Найквіста. Подібно до безперервних систем для дослідження стійкості замкнутих імпульсних систем можна використовувати АФХ розімкнутої системи:
1. Якщо система стійка у розімкнутому стані або нейтральна, тобто має нульові полюси si, то для стійкості замкнутої системи необхідно і достатньо, щоб АФХ розімкнутої системи при змінюванні відносної частоти від 0 до p не охоплювала точку з координатами (-1;j0) і не проходила через неї;
2. Якщо система нестійка у розімкнутому стані, то для стійкості замкнутої системи необхідно і достатньо, щоб АФХ розімкнутої системи при змінюванні відносної частоти від 0 до p охоплювала точку з координатами (-1;j0) k/2 разів, де k – кількість коренів характеристичного рівняння безперервної частини розімкнутої системи, що мають додатну дійсну частину (кількість коренів zi характеристичного рівняння розімкнутої імпульсної системи, модулі яких більші за одиницю).
Тобто формулювання критерію Найквіста для імпульсних систем залишається таким самим, як і для безперервних. Але АФХ імпульсних систем при = p закінчуються на дійсній осі, а не у початку координат.
Зазначимо, що зробити висновок про стійкість розімкнутої імпульсної системи можна на підставі перевірки стійкості її безперервної частини, оскільки полюси передавальних функцій безперервної W(s) та імпульсної W*(s) розімкнутих систем співпадають. Тобто стійкість розімкнутого контуру імпульсної системи визначається стійкістю її безперервної частини. Однак імпульсний елемент суттєво впливає на стійкість і якість замкнутої системи: зі збільшенням періоду квантування Т0 імпульсів у більшості систем зменшується граничний коефіцієнт передачі та погіршуються динамічні властивості. Але на деякі структурно-нестійкі безперервні системи і на системи із запізненням, у яких АФХ потрапляє до першого квадранту, імпульсний елемент впливає як стабілізуючий фактор.
Для таких систем пропонується вибирати Т0 із умови:
Т0³p/wд,
де wд – частота, при якій АФХ безперервної частини розімкнутої системи перетинає додатну уявну піввісь.
Стійкість замкнутої системи можна також визначити за логарифмічними характеристиками – амплітудною L(l) і фазовою j(l). Стосовно логарифмічних характеристик критерій Найквіста формулюється так:
1. Якщо система стійка у розімкнутому стані або нейтральна, то для стійкості замкнутої системи необхідно і достатньо, щоб на частоті зрізу 
, фаза за модулем була менша за p.
2. Якщо система нестійка у розімкнутому стані, то для стійкості замкнутої системи необхідно і достатньо, щоб при 
кількість перетинів фазовою характеристикою рівня -p знизу вгору була в k/2 разів більшою кількості перетинів у протилежному напрямку; k – кількість коренів характеристичного рівняння безперервної частини розімкнутої системи, що мають додатну дійсну частину (кількість коренів zi характеристичного рівняння розімкнутої імпульсної системи, модулі яких більші за одиницю).
Приклад 8.9 Визначити за логарифмічними характеристиками стійкість імпульсної системи, передавальна функція якої наведена у прикладі 8.7:
Полюси передавальної функції розімкнутої системи: z1=1; z2=0,2; z3=0,5. Тому розімкнута система нейтральна (z1=1) і для дослідження стійкості замкнутої системи застосовуємо перше формулювання критерію Найквіста у логарифмічній формі.
Побудову логарифмічних характеристик за передавальною функцією
виконаємо за допомогою пакета Matlab (рис. 8.11).
Рис. 8.11 – Логарифмічні частотні характеристики імпульсної системи
На псевдочастоті зрізу фаза за модулем менша за p і дорівнює 750, тобто система стійка і має запас стійкості за фазою Dj =1050, запас за амплітудою DL = 6дБ.
Якість імпульсних систем
Якість імпульсних систем керування характеризується такими самими показниками, як і якість безперервних систем: точністю регулювання в усталених режимах, тривалістю і перерегулюванням перехідного процесу.
Усталену помилку можна визначити таким самим способом, як і в безперервних системах, тобто знайти зображення помилки з виразу передавальної функції (8.43) замкнутої системи за помилкою:
X(z) = Wx(z)G(z),
і перейти до її усталеного значення згідно з формулою (8.31) для кінцевого значення решітчастої функції:
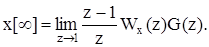(8.57)
Цю формулу не можна застосовувати, коли межа у правій частині не існує, наприклад, коли усталена помилка є гармонічною функцією.
Як і безперервні системи, імпульсні системи можуть бути статичними чи астатичними. Імпульсна система, у якої усталена помилка при будь-якому зовнішньому сигналі дорівнює нулю, називається астатичною по відношенню до цього сигналу. У протилежному разі система називається статичною.
Точність імпульсної системи в усталеному режимі можна оцінювати за коефіцієнтами помилок Сі, які визначаються за формулою:
(8.58)
де
Показники якості перехідних процесів можна визначити розв’язуванням різницевого рівняння, що описує динаміку системи. Для розрахунку перехідної функції (реакції системи на одиничну ступінчасту дію за нульових початкових умов) зручно застосовувати z-перетворення. У цьому разі зображення вхідної величини (табл. 8.1) має вигляд:
G(z) = z/(z-1),
а зображення вихідної – вигляд:
Y(z) = G(z)Wз(z) = Wз(z)×z/(z-1). (8.59)
Оригіналом цієї функції є решітчаста функція y[n]. Якість перехідного процесу визначається за графіком безперервної функції y(t), що відповідає цій решітчастій функції (див. п. 4.2).
Приклад 8.10 Побудувати перехідний процес в імпульсній системі автоматичного регулювання, для якої:
при дії керуючого сигналу g(t) = 1(t) і визначити основні показники якості.
Згідно з (8.42) визначимо передавальну функцію замкнутої імпульсної системи:
Wз(z) = W(z)/[1+W(z)] = 
Тоді відповідно з (8.59) запишемо:
Перехідний процес у системі у тактові моменти часу і основні показники якості можна визначити різними способами. Згідно з одним із них розкладемо отриманий вираз по степенях zi, виконавши ділення чисельника на знаменник. У результаті отримаємо:
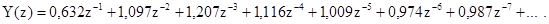
Тоді відповідно до (8.34), (8.35) запишемо:
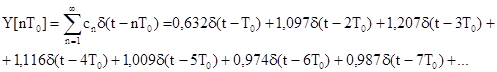
За допомогою цього виразу побудуємо перехідний процес в імпульсній системі (рис. 8.12). З графіка видно, що час регулювання складає 4Т = 0,4 с (після цього моменту відхилення перехідної функції від усталеного значення, що дорівнює одиниці, не перевищує ±5%). Максимальне перерегулювання s = 20,7 % (у момент часу 3Т = 0,3 с).
Якість перехідного процесу можна оцінювати також за полюсами і нулями передавальної функції. Якщо нулі відсутні, то полюси (корені характеристичного рівняння) повністю визначають перехідний процес у системі. У п.8.6 доведено, що для стійкої системи модулі всіх коренів мають бути меншими за одиницю. Коло одиничного радіуса на площині z є відображенням уявної осі на площині s (рис. 8.9). Найбільш істотно на перехідний процес впливають корені, що розміщені найближче до уявної осі площини s, а значить, до кола одиничного радіуса площини z. Такі корені називаються домінуючими.
Якщо система має пару домінуючих комплексно-спряжених коренів 
, а решта коренів знаходиться поблизу початку координат, то час досягнення першого максимуму і перерегулювання визначаються за формулами:
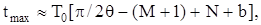(8.60)
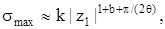(8.61)
де q=arctg(bT0); M–кількість нулів передавальної функції; N– кількість полюсів; b – додатне число (b<1), при якому вираз у квадратних дужках у формулі (8.60) дорівнює цілому числу; k = cos(bq) + [cosec(q/|z1|) – ctgq]sin(bq), 
- модуль домінуючого кореня.
Якість імпульсних систем можна характеризувати також оцінками, подібними до оцінок якості безперервних систем: ступінню стійкості h, коливальністю m (п. 4.5), а також інтегральними оцінками якості (п. 4.6).
Найпростішою з інтегральних оцінок є лінійна інтегральна оцінка:
(8.62)
де y[¥] – усталене значення вихідної величини.
Ця оцінка придатна тільки для неколивальних процесів. Ширше застосування знайшла квадратична оцінка:
(8.63)
Найкращою є та імпульсна система, для якої інтегральні оцінки мінімальні. Значення параметрів системи, що відповідають мінімальним оцінкам, називаються оптимальними за якістю перехідного процесу.
