Решітчасті функції. Вихідний сигнал імпульсного елемента визначається величиною вхідного сигналу тільки у дискретні моменти часу на початку кожного періоду слідування імпульсів і надалі не залежить від змінювання вхідного сигналу до початку наступного періоду слідування (модуляція першого роду). Тому достатньо знати значення вхідного сигналу лише у дискретні моменти часу, тобто у моменти nT0, де n – ціле число. На підставі цього безперервну функцію на вході імпульсного елемента можна замінити так званою решітчастою функцією.
Решітчастою функцією називається функція дискретного аргументу, значення якої визначені у дискретні моменти часу t = nT0. Між цими моментами функція дорівнює нулю. Решітчасту функцію звичайно позначають f [nT0] або, якщо перейти до відносного часу, f [n] (рис. 8.5). Тоді можна записати
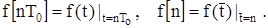
Використовують також поняття зміщеної решітчастої функції. Аргумент цієї функції t = nT0 + Dt, тобто дискретні значення функції вибираються для моментів часу, зміщених на Dt=const відносно nT0. Зміщення може бути додатним або від’ємним, за умови, що |Dt| < Т0. Зміщена решітчаста функція позначається f [nT0, Dt] або, при використанні відносного часу, - f [n, e], де e=Dt/Т0 – відносне зміщення. Надалі будемо вважати, що у решітчастої функції f [n, e] аргумент n> 0 і параметр e>0.
Різниці решітчастих функцій та різницеві рівняння. Різниці решітчастих функцій є аналогами похідних безперервних функцій. Різниця першого порядку (перша різниця) решітчастої функції f [n] дорівнює
Df [n] = f [n+1] - f [n]. (8.10)
Аналогію між першою різницею і першою похідною видно з того, що перша різниця, як і перша похідна дорівнює відношенню приросту функції до приросту аргументу Df [n]/Dn, але через те, що Dn = (n+1)–n = 1, перша різниця дорівнює Df [n].
Різниця другого порядку (друга різниця) обчислюється за формулою
D2f [n] = Df [n+1] - Df [n], (8.11)
або, якщо розкрити перші різниці, за формулою (8.10),
D2f [n] = f [n+2] - 2f [n+1] + f [n]. (8.12)
Різниця k-го порядку має вигляд:
Dkf [n] = Dk-1f [n+1] - Dk-1f [n] = 
(8.13)
де 
- коефіцієнт бінома Ньютона.
Різниці (8.10)-(8.13) називаються прямими. Є також зворотні різниці:
перша
Ñf [n] = f [n] - f [n-1]; (8.14)
друга
Ñ2f [n] = Ñf [n] - Ñf [n-1] = f [n] - 2f [n-1] + f [n-2]; (8.15)
k-го порядку
Ñkf [n] = Ñk-1f [n] - Ñk-1f [n-1] = 
(8.16)
Аналогами інтеграла безперервної функції у межах від 0 до t для решітчастої функції f [n] є неповна сума
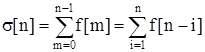(8.17)
і повна сума
(8.18)
У повній сумі, на відміну від неповної, значення f [n] у момент часу t=nT0 також бере участь у формуванні результату.
Аналогами диференціальних рівнянь є різницеві рівняння (рівняння у кінцевих різницях). Лінійні різницеві рівняння зі сталими коефіцієнтами при використанні прямих різниць мають вигляд:
b0Dmy[n] + b1Dm-1y[n] + … + bmy[n] = f [n], (8.19)
де f [n], y[n] – відповідно задана і шукана решітчасті функції.
Якщо f [n] º 0, то рівняння (8.19) називається однорідним.
Приклад 8.1 Отримати різницеве рівняння з диференціального рівняння:
З урахуванням (8.10) і (8.12) запишемо:
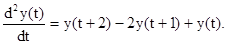
Тоді задане рівняння матиме вигляд:
або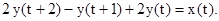 
Для розв’язування різницевих рівнянь (8.19) необхідно задавати початкові умови у вигляді значень шуканої функції y[n] та її різниць від першої до різниці (m-1)–го порядку.
Різницеві рівняння можна розглядати як рекурентні співвідношення, які дають змогу обчислювати значення y[n] при n =1, 2, 3, … для заданих початкових умов. З урахуванням (8.13) рівняння (8.19) матиме вигляд:
a0y[n+m] + a1y[n+m-1] + … + amy[n] = f [n], (8.20)
де 
Наприклад, якщо задане різницеве рівняння (8.20) третього порядку:
a0y[n+3] + a1y[n+2] + a2y[n+1]+a3y[n] = f [n],
і відомі функції f [n] та початкові умови y[0], y[1], y[2], то дискретні значення функції y[n] обчислюються так:
при n=0: a0y[3] + a1y[2] + a2y[1]+a3y[0] = f [0],
y[3] = (f [0] - a1y[2] - a2y[1] - a3y[0]) / a0;
при n=1: a0y[4] + a1y[3] + a2y[2]+a3y[1] = f [1],
y[4] = (f [1] - a1y[3] - a2y[2] - a3y[1]) / a0;
і т.д.
Рівняння (8.19) є більш близьким аналогом диференціального рівняння, однак рівняння (8.20) легше використовувати, і тому воно більш розповсюджене.
Різницеві рівняння можна розв’язувати також класичним і операторним методами, аналогічними методам розв’язування диференціальних рівнянь. З операторних методів найбільшого поширення набув метод, що ґрунтується на використанні z-перетворення.
Основи z - перетворення. Дискретну функцію f [nT0] можна аналітично записати у вигляді ряду:
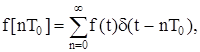(8.21)
де f(t) – породжувальна безперервна функція;
d(t-nT0) – зміщена на час nT0 дельта-функція.
Перетворення Лапласа від функції (8.21) має вигляд:
(8.22)
Це перетворення називається дискретним перетворенням Лапласа. У символічній формі його записують так:
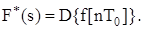
Якщо аргументом безперервної функції є відносний час t/T0, то формула дискретного перетворення матиме вигляд:
(8.23)
де q=sT0 – комплексне число, яке називається параметром дискретного перетворення Лапласа.
Зображення F*(s) і F*(q) є трансцендентними функціями від s і q, що робить неможливим застосування звичайних методів аналізу в площині s або q для дослідження імпульсних систем. Більш прийнятним є z - перетворення. Формула z–перетворення випливає з формули (8.23), якщо виконати підстановку eq = z. Вона має вигляд:
(8.24)
Приклад 8.2 Визначити z-перетворення одиничної решітчастої функції f[n]=1[n].
За формулою (8.24) запишемо
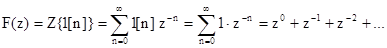
Сума цієї геометричної прогресії: 
z- перетворення деяких функцій подано в таблиці 8.1.
Таблиця 8.1 - z- перетворення основних функцій
| Безперервна функція f(t) | Решітчаста функція f [n] | Перетворення Лапласа F(s) | z-перетворення F(z) |
| 1(t) | 1[n] | 1/s | z/(z-1) |
| t | nT0 | 1/s2 | T0z / (z-1)2 |
| t2 | (nT0)2 | 2/s3 | T0 2z(z+1) / (z-1)3 |
| t3 | (nT0)3 | 6/s4 | T0 3z(z2+4z+1) / (z-1)4 |
| e-at |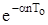 
| 1/(s + a) | z/(z-d), d = 
|
| 1 - e-at | 
| a/[s(s+a)] | (1-d)z / [(z-1)(z-d)], d =
|
| sin bt | sin bnT0 | b/(s2 + b2) | z×sin bT0/(z2 - 2z×cos bT0 + 1) |
Розглянемо основні властивості z-перетворення стосовно незміщених решітчастих функцій.
1. Властивість лінійності. Зображення лінійної комбінації решітчастих функцій дорівнює такій самій лінійній комбінації їх зображень.
2. Запізнювання і випередження (зсув за часом на ціле число періодів). Для решітчастої функції, зсунутої вправо (запізнюючої) на m періодів, маємо:
Z{f [n-m]}= z-mF(z), (8.25)
де F(z) – зображення функції f [n].
Для решітчастої функції, зсунутої вліво (випереджуючої) на m періодів, маємо:
Z{f [n + m]}=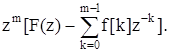 
(8.26)
3. Множення оригіналу на експоненту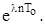 
Зображення незміщеної решітчастої функції записуємо у вигляді:
(8.27)
4. Зображення різниць (аналог зображення похідної). Для різниці k-го порядку за нульових початкових умов, тобто n=0, маємо:
Z{Dk f [n]} = (z-1)k F(z), (8.28)
звідки для першої різниці (k=1)
Z{D f [n]} = (z-1) F(z).
5. Зображення суми (аналог зображення інтеграла). Зображення суми має вигляд:
(8.29)
6. Початкове значення решітчастої функції. При n=0 значення решітчастої функції обчислюється за формулою:
(8.30)
7. Кінцеве значення решітчастої функції. При n = ¥ запишемо:
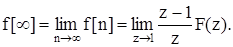(8.31)
8. Згортка решітчастих функцій. Якщо
Z{f1[n]} = F1(z) і Z{f2[n]} = F2(z),
то
F1(z)F2(z) = 
(8.32)
9. Зображення функції 
Маємо
Z{F(s)} = F1(z) Z{F2(s)}. (8.33)
За допомогою z-перетворення можна розв’язувати різницеві рівняння, причому послідовність дій аналогічна послідовності розв’язування диференціальних рівнянь при використанні перетворення Лапласа безперервних функцій. Спочатку треба перейти від різницевих рівнянь відносно оригіналів до алгебраїчних рівнянь відносно їх z-зображень, потім визначити z-зображення шуканої функції, розв’язавши знайдене алгебраїчне рівняння, і нарешті перейти від z-зображення до оригіналу – шуканої решітчастої функції.
Для переходу до оригіналу зображення доцільно подати у вигляді простих дробів, для яких оригінали можна знайти у таблицях z-перетворень функцій часу, і знайти оригінал y[n] як суму оригіналів, що відповідають простим дробам.
Значення функції y[n] у дискретних точках можна обчислити без знаходження аналітичного виразу для неї, якщо розкласти зображення Y(z) в ряд Лорана
Y(z) = c0 + c1z-1 + c2z-2 + c3z-3 + … (8.34)
За формулою (8.24) отримаємо:
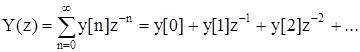(8.35)
Із (8.34) і (8.35) випливає, що y[0] = c0, y[1] = c1, y[2] = c2 і т.д.
Найзручнішим способом розкладання в ряд Лорана дрібно-раціональних функцій є ділення чисельника на знаменник.
Приклад 8.3 За відомим z-перетворенням Y(z) = 3z/(z2 – 0,7z + 0,1) визначити оригінал y[n].
Розкладемо Y(z) на суму простих дробів. Для цього визначимо корені рівняння z2 – 0,7z + 0,1 = 0. Маємо z1=0,5; z2=0,2. Тоді можна записати:
Y(z) = 3z/(z – 0,5)(z - 0,2) = 10[z / (z-0,5) – z / (z-0,2)].
З таблиці 8.1 знаходимо, що доданку z/(z-0,5) відповідає оригінал 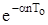, де =d = z1 = 0,5. Тобто оригінал має вигляд 0,5n Аналогічно для доданка z/(z-0,2) маємо оригінал 0,2n. Отже, шукана решітчаста функція має вигляд:
y[n] = 10(0,5n - 0,2n).
Звідси знаходимо дискретні значення функції y[n]: y[0] = 0; y[1] = 3; y[2] = 2,1; y[3] = 1,17 і т.д.
Визначимо тепер дискретні значення функції y[n], розклавши зображення Y(z) в ряд Лорана діленням чисельника на знаменник:
3z / (z2 – 0,7z + 0,1) = 3z-1 + 2,1z-2 + 1,17z-3 + …
Отже, Y(z) = 0 + 3z-1 + 2,1z-2 + 1,17z-3 + …, тобто y[0] = 0; y[1] = 3; y[2] = 2,1; y[3] = 1,17.
