Здесь будет доказана одна из центральных теорем теории функций комплексной переменной. Используя теорему Коши, можно установить связь между значениями аналитической функции в любой внутренней точке области со значениями этой функции на контуре, охватывающем эту точку.
Теорема 6. Пусть функция f(z) аналитическая в односвязной области D, точка z0 внутренняя точка области D, C - замкнутый контур, целиком лежащий в D и содержащий внутри себя точку z0. Тогда справедлива формула:
. (4)
Интеграл, стоящий в правой части называется интегралом типа Коши, а выражение (4) – интегральной формулой Коши.
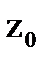
| D |
| С |
Рис.8.
□ Рассмотрим окружность 
с центром в точке z0, целиком лежащую в D. Между контурами C и CR функция 
аналитическая и по следствию к теореме 4 выполняется равенство:
.
Интеграл в левой части не зависит от радиуса R, тогда и в правой части интеграл также не зависит от радиуса. Теперь можно записать:
.
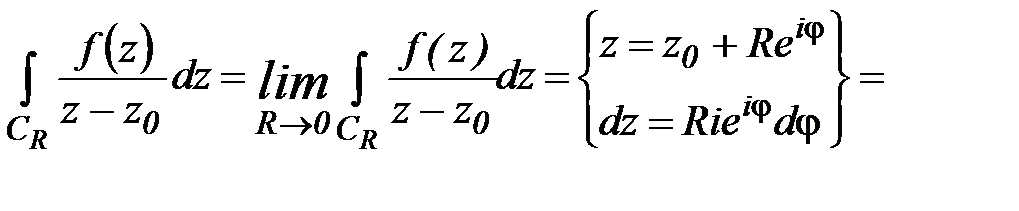
Последнее равенство справедливо в силу непрерывности функции f(z). Если теперь разделить обе части на 
, получим формулу (4). ■
Замечание 1. Теорема будет справедлива и для многосвязной области, если f(z) непрерывна в замыкании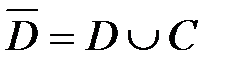 
, где С - граница многосвязной области.
Замечание 2. Интегральную формулу (4) можно использовать для вычисления интегралов по замкнутому контуру, а именно:
если 
;
если 
.
Пример 5. Вычислить интеграл: 
.
Решение.
В интеграле Коши интегрирование выполняется по переменной z, тогда z0 является параметром в этом интеграле, т.е. интеграл Коши это интеграл, зависящий от параметра.
Теорема 7 (дифференцирование интеграла по параметру). Пусть выполняются условия:
1) L - кусочно-гладкая кривая и 
;
2) точка 
принадлежит области D;
3) функция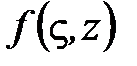 
и 
являются непрерывными функциями по совокупности переменных;
4) функция 
при 
является аналитической в области D.
Тогда функция 
является аналитической в области D и её производная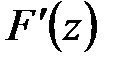 
представляется в виде:
.
□ Введем скалярные обозначения: 
Рассмотрим криволинейные интегралы:
По условию теоремы 3, функции u,v обладают частными производными по x,y,непрерывными по совокупности переменных, поэтому частные производные функции U(x,y) и V(x,y) существуют по переменным x,y и их можно вычислить при помощи дифференцирования под знаком интеграла. Тогда получим:
, 
.
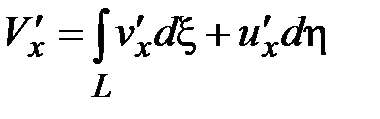
Производные 
являются непрерывными функциями по x,y в D. Используя условие Коши-Римана для функции 
получим:
.
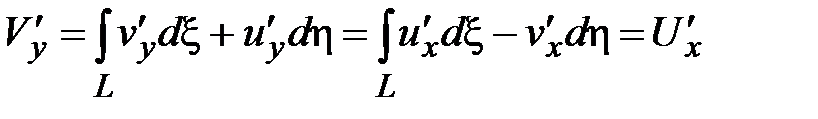Таким образом, для действительной и мнимой частей функции 
выполняются условия Коши-Римана, следовательно, она является аналитической. Кроме того,
.
Объединяя два интеграла, получим производную: 
. ■
Интеграл Коши устанавливает зависимость между значением аналитической в D функции f(z) в точке 
c значениями этой функции на контуре, охватывающем точку 
причем f(z) на контуре может быть не аналитической, а только непрерывной. Поэтому естественно поставить вопрос об изучении свойств функции
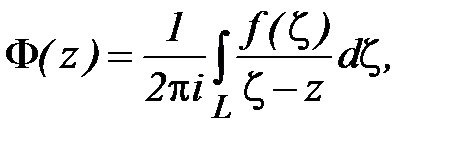(5)
где L непрерывная кусочно-гладкая (не обязательно замкнутая) кривая, f(ζ) непрерывна на кривой, а 
Функция 
параметра z, определенная соотношением (5), называется интегралом типа Коши.
Теорема 8. Если функция f(z) аналитическая в области D и непрерывна на кусочно-гладкой кривой L, то функция 
также является аналитической в D, не содержащей точек кривой L и справедлива формула:
. (6)
Более того, у функции 
в области D существуют производные любого порядка, определяемые по формуле
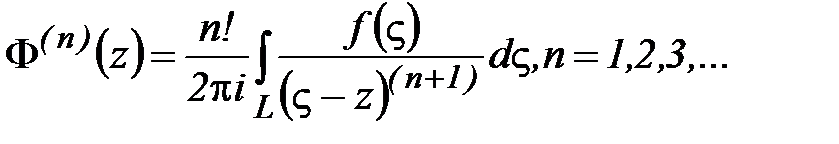(7)
□ Рассмотрим вспомогательные функции: 
, k=1,2.3… Эти функции непрерывны всюду, кроме точек кривой L, т.е. для них выполняются все условия теоремы 7, согласно которой для k=1 можно записать:
Продолжая дифференцировать по индукции, получим формулу (7). ■
Так как формула Коши
где 
, является частным случаем интеграла типа Коши, то из теоремы вытекает важное для всей теории аналитических функций следствие.
Следствие. Если функция f(z) аналитическая в области D, то она имеет в этой области производную любого порядка, которые являются также аналитическими функциями в этой области и определяются равенствами:
(8)
Эта формула справедлива, если в равенстве (7) в качестве Ф(z) взять f(z), а интегрирование выполнить по замкнутому контуру С, целиком лежащем в D и содержащем внутри себя точку z. Из (8) можно получить еще одну формулу вычисления контурных интегралов:
;
Пример 5. Вычислить интеграл 
Решение.
