ГЛАВА 1. ОПРЕДЕЛИТЕЛИ.
Числовые кольца и поля.
R - множество действительных чисел.
К - подмножество действительных чисел.
К называется числовым кольцом если для любых двух элементов а и b 
: Сумма а+b, разность a-b, произведение ab принадлежат К.
Примеры:
1) К= {0}
2) K= Q = { 
| m 
{0,+-1, +-2,...}, n {1,2,3,...}
3) K=R
4) 2Z={2*n | n Z}
Свойства числовых колец.
1) Любое числовое кольцо содержит 0.
a 
K, a-a= 0 K
Следствие:
Нулевое кольцо является наименьшим и содержится в любом числовом кольце.
2) Если a K, то для любого целого n: n*a K
n=0; n*a=0
n>0; n*a= a+a+a+...+a K
n<0; m=-n; n>0 n*a=-m*a= (-a)+(-a)+(-a)
Следствие
Любое ненулевое ЧК содержит бесконечное число элементов.
m*a=n*a
a 
0, если сократить на а, то m=n
Числовое поле.
Опр. Непустое множество К, являющееся не 0 числовым кольцом, называется числовым полем, если для любого a,b K: b 
; 
K- числовое поле a, b, a+b, a-b, ab K; a,b 0; 
K
Примеры числовых полей.
1) Q
2) R
3) K = {a+b 
|a,b Q}
1 / = a+ b
Теорема. Поле рациональных чисел Q содержится в любом числовом поле К.
Доказательство:
Так как К - это ненулевое числовое поле то есть один элемент а и а 0
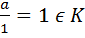
n= 1+1+...+1 
-n
Z 
n/m n,m 
и m 0
Q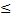 
K. Теорема доказана.
Перестановки.
Если М - конечное множество
M = {1,2,..., n}
Опр. Любое расположение чисел {1,2,...,n} в каком то порядке называется перестановкой.
M={1,2,3}
(2,1,3), (1,2,3), (3,2,1), (1,3,2)
(
Теорема. Количество различных перестановок n-элемента равно n!=n(n-1)
Доказательство: Рассмотрим произвольную перестановку:
(
Количество выбора различных элементов 
= n, а разных способов выбора 
Пара (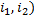
выбирается n(n-1) числом способов.
Опр. Говорят, что i,j образуют инверсию если i>j, а в перестановке (i,..., j)
(4,1,3,2): (4,1) - инверсия, (1,3) - не инверсия.
Опр. Перестановка называется четной, если количество инверсий в перестановке равно четному числу, иначе - нечетная.
Опр. Транспозицией элементов i,j называется такое преобразование перестановки при котором i,j меняются местами.
Теорема. При транспозиции перестановка меняет свою четность на противоположную.
Доказательство.
1 случай.
Пусть i,j - соседние элементы перестановки
(.....i,j.....)
(....,j,i.....)
Пары, которые не содержат i,j:
(
- такие пары в 1 и 2 перестановке одинаковы.
(
- где один элемент равен i
(
останутся одинаковыми для 1 и 2 перестановки, аналогично пары содержащие элемент j
В первой (i;j)
Во второй (j;i)
S - количество инверсий в парах отличных от пары (i,j).
Пусть i,j образуют инверсию, тогда i,j - не является инверсией => в 1 перестановке число инверсий S+1, а во второй S. Чтд.
2 случай.
Лень писать все формулы, смотрите в тетради.
Пусть i,j не соседние
Каждый раз меняется четность, т.к. количество смен четности - нечетное число, то первая и последняя перестановки имеют разную четность.
Следствие. Число четных и нечетных перестановок одинаковое число 
Док-во писать лень.
Матрицы и определители.
Квадратной матрицей порядка n называется таблица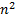 
чисел, записанная в n строк и n столбцов.
Опр. Транспонированием матрицы А называется такое преобразование при котором строчки располагаются в столбцы.
Опр. Определителем n-ного порядка, соответствующего квадратной матрице А называется алгебраическая сумма n! слагаемых, каждый из которых состоит из произвольных n элементов матрицы А, взятых по одному из каждой строки и столбца, взятых со знаком + если перестановка вторых индексов является четной, и со знаком -, если нечетной, при условии что первый индекс располагается в естественном порядке.
Свойства определителя.
Равноправие строк и столбцов.
Величина определителя не меняется при транспонировании.
Если определитель обладает свойством относительно строчек, то он обладает тем же свойством относительно столбцов.
2) Переменность: Если поменять 2 строки местами, то знак меняется на противоположный.
3) Еслив определителе две строчки равны то такой определитель равен нулю.
4) Однородность: Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k.
5) Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю.
6)Пропорциональность: Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю
7) Аддитивность: Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же.
Свойство 7 верно если число строчек больше двух.
Опр. i-строка определителя является линейной комбинацией остальных её строк если существуют такие константы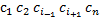 
что i-строчка равняется сумме:
(i)= 
8) Если одна из строк определителя является линейной комбинацией других его строк, то такой определитель равен нулю.
9) Величина определителя не изменится если к некоторой строчке прибавить другую строчку умноженную на константу.
