Слегка изменим эксперимент с красными и белыми бусинами, описанный в Главе 11 на стр. 356, чтобы за несколько минут продемонстрировать нулевую корреляцию между количеством дефектных единиц в выборках, взятых из партии и количеством дефектных единиц в остатке.
Математическое доказательство содержится в Уравнении 4 Упражнения 1 на стр. 453. Тот же самый эксперимент покажет наличие слабой корреляции между выборками и партиями.
Необходимо всего лишь поделить партию из 50 бусин в эксперименте на 2 части так, чтобы одна часть представляла выборку, а вторая - остаток (рис. 56). Сосчитайте и запишите количество красных бусин в выборке и остатке каждой партии, затем верните все 50 бусин в исходную емкость. Перемешайте их и изымите новую партию.
Нам помогут некоторые специальные обозначения. Мы будем получать партии постоянной величины М с дефектными единицами, биноминально распределенными вблизи средней величины р. Возьмите без замещения из каждой партии выборку стандартной величины п. Сосчитайте дефектные единицы в каждой выборке и каждом остатке. Пусть s будет количеством дефектных единиц в выборке, а r — их количеством в остатке (как это делалось выше). Тогда s и r будут случайными переменными величинами, смешанное распределение которых показано в Уравнении 4 на стр. 453. Пусть
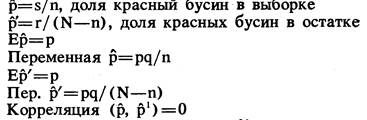
Переменные p уменьшаются по мере увеличения N и n. Отсюда следует, что большая выборка, взятая из большой партии, дает информацию о дефектных единицах в остатках, следовательно, о дефектных единицах также и в партиях.
Более того, мы можем применить к указанной проблеме (целью которой является выявление характеристик партий через выборки) теорию выборки для оценки характеристик партий, а также для оценки стандартных ошибок этих оценок.
Обратимся теперь к некоторым реальным результатам, полученным при селекции партии и выборке определенных размеров. Рис. 57 58, 59 и 60 показывают пропорцию красных бусин в биноминальных выборках и остатках для выбранных величин N и n (которые любезно рассчитал мой друг Бенджамин Дж. Теплинг на своем компьютере). Собственно говоря, как выборка, так и остаток являются выборками одной и той же партии. В каждом графике 100 выборок. Эти графики отчетливо иллюстрируют нулевую корреляцию между выборкой и остатком. Однако, чем больше выборка, тем надежнее оценка пропорции красных бусин в выборках и остатках. Так, рис. 60, где выборка имеет объем n =1000 и остаток N—п = 9000, ясно показывает, что крупная выборка обеспечивает лучшую оценку содержания, как остатка, так и всей структуры (выборка плюс остаток) — в данном случае, емкости с красными и белыми бусинами, даже если выборка и остаток не коррелированы. Поразительной особенностью статистической теории является ее способность подсчитать, на основе единственной выборки, если она достаточно большого объема, размер футбольного мяча, на рис. 57—60, который содержит в среднем, скажем, около 95% всех точек. Таким образом, теория выборки позволяет производить оценку характеристик остатка и целой партии, а также стандартных ошибок этих оценок.

Рис. 57 N = 50 п = 20 Здесь образец и остаток не очень разнятся по размерам, соотносясь как 20 и 30 соответственно. Таблица не отражает какой взаимосвязи между соотношением красных шариков в образце и соотношением красных шариков в остатке.

Рис. 58 N = 600, п = 20 Здесь изменения в соотношении красных шариков в остатке явно намного меньше, чем изменения в образце. Причина в том, что остаток имеет размеры N- n = 600-20=580, во много раз отличается от размеров образца. Здесь опять взаимосвязь между соотношением красных шариков в образце и соотношением красных шариков в остатке оказывается равной нулю.

Рис. 59. N = 600, n = 200. Здесь мы видим, что получается, когда мы увеличиваем размеры образца до 200 и уменьшаем остаток до 400. Эта таблица, как и ранее, иллюстрирует нулевую взаимосвязь между соотношением красных шариков в. остатке.

Рис. 60. N = 10,000, п = 1000 Опять нет взаимосвязи.






