Вариант 1
Часть1
| Модуль «Алгебра» |
1. Запишите в ответе номера выражений, значения которых положительны.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
1) 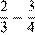
| 2) 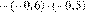
| 3) 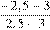
| 4) 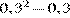
|
Решение.
Найдём значения выражений:
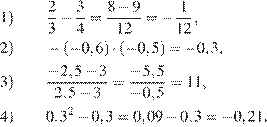
Таким образом, искомое выражение указано под номером 3.
Ответ: 3
2. Известно, что 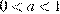 . Выберите наибольшее из чисел.
. Выберите наибольшее из чисел.
1) 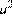 2)
2) 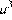 3)
3) 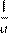 4)
4) 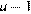
Решение.
Поскольку 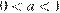 число
число  отрицательно,
отрицательно, 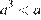 и
и 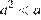 . Число
. Число 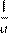 положительно и больше 1. Поэтому оно является наибольшим.
положительно и больше 1. Поэтому оно является наибольшим.
Правильный ответ указан под номером 3.
Ответ: 3
3. В какое из следующих выражений можно преобразовать дробь  ?
?
1)  2)
2) 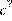 3)
3) 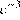 4)
4) 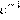
Решение.
Упростим дробь:

Правильный ответ указан под номером 3.
Ответ: 3
4. Решите уравнение 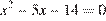 .
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
По теореме, обратной теореме Виета — сумма корней равна 5, а их произведение равно −14.
Тем самым, это числа −2 и 7.
Ответ: −2; 7.
Ответ: -2; 7
5. Установите соответствие между графиками функций и формулами, которые их задают.
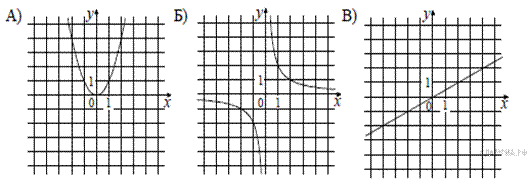
1) 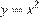 2)
2) 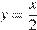 3)
3) 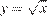 4)
4) 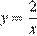
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
| А | Б | В |
Решение.
Определим вид графика каждой из функций.
1) 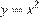
 уравнение параболы, ветви которой направленны вверх.
уравнение параболы, ветви которой направленны вверх.
2) 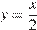
 уравнение прямой.
уравнение прямой.
3) 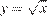
 уравнение верхней ветви параболы, направленной вправо.
уравнение верхней ветви параболы, направленной вправо.
4) 
 уравнение гиперболы.
уравнение гиперболы.
Тем самым найдено соответствие: A — 1, Б — 4, В — 2.
Ответ: 142.
Ответ: 142
6. Дана арифметическая прогрессия 14, 9, 4,... Какое число стоит в этой последовательности на 81-м месте?
Решение.
Определим разность арифметической прогрессии:
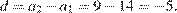
Член арифметической прогрессии с номером 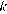 может быть найден по формуле
может быть найден по формуле
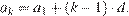
Поэтому 
Ответ: 414.
Ответ: 414
7. Найдите значение выражения 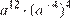 при
при 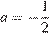 .
.
Решение.
Упростим выражение:

При 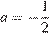 , значение полученного выражения равно 16.
, значение полученного выражения равно 16.
Ответ: 16.
Ответ: 16
8. Решите систему неравенств 
| Модуль «Геометрия» |
На каком из рисунков изображено множество её решений?
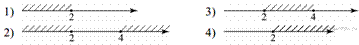
Решение.
Решим систему:

Правильный ответ указан под номером 3.
Ответ: 3
9. В выпуклом четырехугольнике ABCD  ,
,  ,
,  ,
, 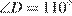 . Найдите угол A. Ответ дайте в градусах.
. Найдите угол A. Ответ дайте в градусах.
Решение.
Сумма углов выпуклого четырёхугольника равна 360°. Имеем: 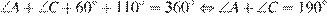 Так как
Так как  ,
,  и
и 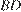 — общая треугольника ABD и BDC. Из равенства треугольников следует, что
— общая треугольника ABD и BDC. Из равенства треугольников следует, что  . Таким образом,
. Таким образом,  .
.
Ответ: 95.
Ответ: 95
10.  Найдите
Найдите  , если градусные меры дуг
, если градусные меры дуг 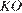 и
и 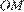 равны 112° и 170° соответственно.
равны 112° и 170° соответственно.
Решение.
Так как вписанный угол равен половине дуги на которую он опирается, имеем 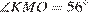 , а
, а 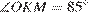 . В треугольнике OKM,
. В треугольнике OKM,  .
.
Ответ: 39.
Ответ: 39
11. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на 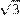 .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними, имеем:
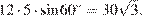
Ответ: 30.
----------
В открытом банке иррациональный ответ.
Ответ: 30
12  На квадратной сетке изображён угол
На квадратной сетке изображён угол 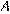 . Найдите
. Найдите  .
.
Решение.
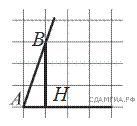
Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,
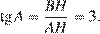
Ответ: 3.
Ответ: 3
13. Какие из следующих утверждений верны?
1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.
4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
| Модуль «Реальная математика» |
Решение.
Проверим каждое из утверждений.
1) «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.» — неверно, квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2) «Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.» — верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
3) «Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.» — верно, остроугольным называется треугольник у которого все углы меньше 90°.
4) «В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.» — верно, по теореме Пифагора.
Ответ: 2; 3; 4.
Ответ: 2; 3; 4
14 В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.

Какой вывод о суточном потреблении углеводов мужчиной можно сделать, если по подсчётам диетолога в среднем за сутки он потребляет 488 г углеводов?
1) Потребление в норме.
2) Потребление выше рекомендуемой нормы.
3) Потребление ниже рекомендуемой нормы.
4) В таблице недостаточно данных.
Решение.
Суточная норма потребления углеводов мужчины лежит в пределах 257−586 г. Потребление 488 г жиров в сутки соответствует норме.
Правильный ответ указан под номером 1.
Ответ: 1
15. На рисунке изображен график движения автомобиля из пункта  в пункт
в пункт  и автобуса из пункта
и автобуса из пункта 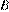 в пункт
в пункт 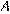 . На сколько километров в час скорость автомобиля больше скорости автобуса?
. На сколько километров в час скорость автомобиля больше скорости автобуса? 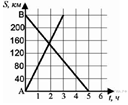
Решение.
Автобус проехал 240 км за 5 часов. Таким образом, его скорость равна 48 км/ч. Автомобиль проехал это же расстояние за 3 часа со скоростью 80 км/ч. Таким образом, скорость автомобиля больше скорости автобуса на 32 км/ч.
Ответ: 32
16. На многопредметной олимпиаде 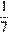 всех участников получили дипломы,
всех участников получили дипломы,  остальных участников были награждены похвальными грамотами, а остальные 144 человека получили сертификаты об участии. Сколько человек участвовало в олимпиаде?
остальных участников были награждены похвальными грамотами, а остальные 144 человека получили сертификаты об участии. Сколько человек участвовало в олимпиаде?
Решение.
Все участвовавшие в олимпиаде делятся на три группы: участники, получившие дипломы, участники, получившие сертефикаты, участники, получившие похвальные грамоты. Известно что 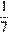 всех участников получили дипломы, следовательно, оставшаяся часть составила
всех участников получили дипломы, следовательно, оставшаяся часть составила 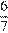 от общего числа участников. Из участников, получивших дипломы,
от общего числа участников. Из участников, получивших дипломы,  участников были награждены похвальными грамотами, оставшиеся
участников были награждены похвальными грамотами, оставшиеся 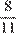 участников составили 144 человека. Пусть x — общее число участников, тогда:
участников составили 144 человека. Пусть x — общее число участников, тогда:
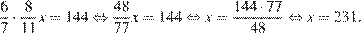
Тем самым, в олимпиаде участвовал 231 учащийся.
Ответ: 231.
Ответ: 231
17. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м? 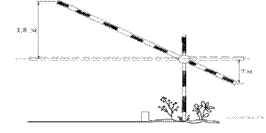
Решение.
Найдём синус угла, на который поднимается длинное плечо:
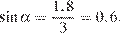
Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:

Таким образом, короткое плечо опустится на 0,6 м.
Ответ: 0,6.
Ответ: 0,6
18 На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей. Какое из следующих утверждений неверно?
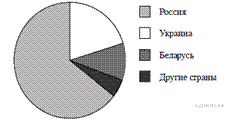
1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе.
2) Пользователей из Украины больше, чем пользователей Латвии.
3) Примерно две трети общего числа пользователей — из России.
4) Пользователей из Украины больше 3 миллионов.
В ответ запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа:
1) Очевидно, что пользователей из России больше, чем пользователей из Украины и Белоруссии вместе.
2) Сектор «Украина» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Латвия» включена в «Другие страны», имеем: пользователей из Украины больше, чем пользователей из Латвии.
3) Сектор в две трети диаграммы отсекается углом в 2·360°/3 = 240°. Очевидно, что угол, отсекающий сектор «Россия» примерно равен 240°, значит примерно две трети общего числа пользователей — из России.
4) Видно, что пользователей из Украины меньше четверти всех пользователей, значит, меньше 12/4=3 миллионов.
Ответ: 4.
Ответ: 4
19. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение.
Вероятность благоприятного случая(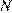 ) — отношение количества благоприятных случаев к количеству всех случаев. В данной задаче благоприятным случаем является старт спортсмена не из России под номером 1. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно
) — отношение количества благоприятных случаев к количеству всех случаев. В данной задаче благоприятным случаем является старт спортсмена не из России под номером 1. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно 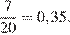
Ответ: 0,35.
Ответ: 0,35
20. Площадь трапеции 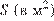 можно вычислить по формуле
можно вычислить по формуле 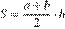 , где
, где 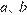 — основания трапеции,
— основания трапеции,  — высота (в метрах). Пользуясь этой формулой, найдите высоту
— высота (в метрах). Пользуясь этой формулой, найдите высоту  , если основания трапеции равны
, если основания трапеции равны 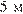 и
и 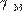 , а её площадь
, а её площадь 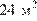 . Часть 2
. Часть 2
Решение.
Выразим высоту трапеции из формулы площади:
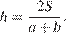
Подставляя, получаем:
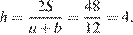
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:

Ответ: 4
21. Разложите на множители 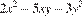 .
.
Решение.
Имеем:
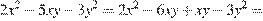
 .
.
Ответ: 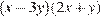 .
.
22. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение.
Пусть первый оператор может выполнить данную работу за  часов, а второй за
часов, а второй за  часов. За один час первый оператор выполняет
часов. За один час первый оператор выполняет 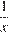 часть всей работы, а второй
часть всей работы, а второй 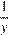 . Составим систему уравнений:
. Составим систему уравнений:

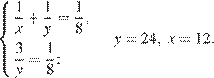
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.
23. Найдите наименьшее значение выражения и значения  и
и  , при которых оно достигается:
, при которых оно достигается: 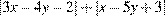 .
.
Решение.
Сумма 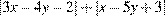 принимает наименьшее значение, равное 0, только в том случае, когда оба слагаемых одновременно равны 0. Получаем систему уравнений
принимает наименьшее значение, равное 0, только в том случае, когда оба слагаемых одновременно равны 0. Получаем систему уравнений
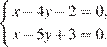
Решим её:
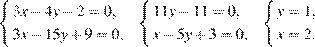
Ответ: 0; (2;1).
24.  Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Решение.
 Проведём радиус OA. Треугольник AOC — прямоугольный, ∠ A = 90°. ∠ COA = 180° − ∠ AOD = 180° − 140° = 40°; ∠ ACO = 90° − 40° = 50°.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠ A = 90°. ∠ COA = 180° − ∠ AOD = 180° − 140° = 40°; ∠ ACO = 90° − 40° = 50°.
Ответ: 50.
25.  В окружности с центром
В окружности с центром  проведены две равные хорды
проведены две равные хорды 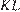 и
и 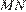 . На эти хорды опущены перпендикуляры
. На эти хорды опущены перпендикуляры 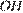 и
и  . Докажите, что
. Докажите, что 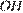 и
и 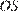 равны.
равны.
Решение.
Проведем ОK, ON, ON, OM - радиусы. Треугольники KOL и MON равны по трем сторонам, тогда высоты OH и OS также равны как элементы равных треугольников. Что и требовалось доказать.
26. Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AM
Вариант 2
Часть1
| Модуль «Алгебра» |
1. Укажите наименьшее из следующих чисел:
1) 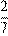
| 2) 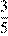
| 3) 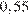
| 4) 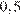
|
Решение.
Заметим что 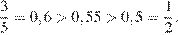 Поскольку
Поскольку 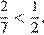 число
число 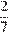 является наименьшим.
является наименьшим.
Таким образом, правильный ответ указан под номером 1.
Ответ: 1
2 На координатной прямой отмечены числа  ,
, 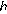 ,
,  . Какой из следующих утверждений неверно?
. Какой из следующих утверждений неверно?
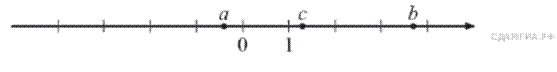
1) 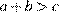 2)
2) 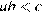 3)
3)  4)
4) 
Решение.
Заметим, что 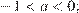
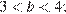
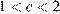 и
и 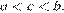 Проверим все варианты ответа:
Проверим все варианты ответа:
1)  — верно, так как
— верно, так как 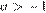 , а
, а 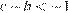 ;
;
2) 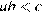 — верно, так как
— верно, так как 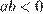 , а
, а 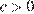 ;
;
3)  — неверно, так как
— неверно, так как  ;
;
4)  — верно, см. случай 1).
— верно, см. случай 1).
Правильный ответ указан под номером 3.
Ответ: 3
3. Какое из следующих выражений равно 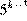
1)  2)
2) 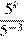 3)
3)  4)
4) 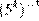
Решение.
При делении степеней с одинаковыми основаниями их показатели вычитаются. Таким образом, правильный ответ под номером 1.
Ответ: 1
4. Решите уравнение 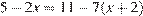 .
.
Решение.
Последовательно получаем:
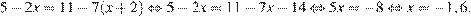
Ответ: −1,6.
Ответ: -1,6
5. Установите соответствие между графиками функций и формулами, которые их задают.
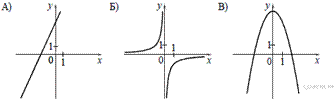
1) 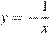 2)
2) 
3) 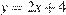 4)
4) 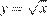
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
| А | Б | В |
Решение.
Определим вид графика каждой из функций.
1) 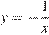
 уравнение гиперболы.
уравнение гиперболы.
2) 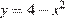
 уравнение параболы, ветви которой направленны вниз.
уравнение параболы, ветви которой направленны вниз.
3) 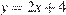
 уравнение прямой.
уравнение прямой.
4) 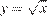
 уравнение верхней ветви параболы, направленной вправо.
уравнение верхней ветви параболы, направленной вправо.
Тем самым найдено соответствие: A — 3, Б — 1, В — 2.
Ответ: 312.
Ответ: 312
6. Дана арифметическая прогрессия (аn): −6, −2, 2, …. Найдите a 16.
Решение.
Определим разность арифметической прогрессии:

Член арифметической прогрессии с номером 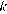 может быть найден по формуле
может быть найден по формуле
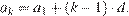
Необходимо найти  , имеем:
, имеем:

Ответ: 54.
Ответ: 54
7. Найдите значение выражения
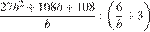 при
при 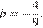
Решение.
Упростим выражение:
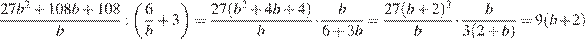 (при
(при 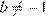 и
и 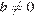 ).
).
Найдём значение выражения при 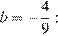
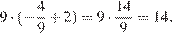
Ответ: 14.
Ответ: 14
8. Решение какого из данных неравенств изображено на рисунке? 
1) 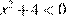 2)
2) 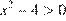
3) 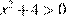 4)
4) 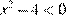
| Модуль «Геометрия» |
Решение.
Решим каждое из неравенств:
1) 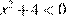 — решений нет.
— решений нет.
2) 
3) 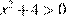 — верно для всех
— верно для всех 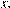
4) 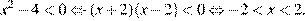
Правильный ответ указан под номером 4.
Ответ: 4
9. 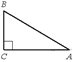 В треугольнике ABC угол C прямой, BC =3, cos B = 0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC =3, cos B = 0,6. Найдите AB.
Решение.
В прямоугольном треугольнике:
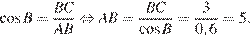
Ответ: 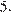
Ответ: 5
10. 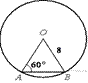 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Решение.
В треугольнике 
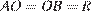 (
(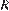 — радиус окружности), следовательно треугольник
— радиус окружности), следовательно треугольник  — равнобедеренный, то есть
— равнобедеренный, то есть 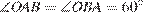 . Найдём угол
. Найдём угол 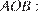
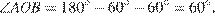
Заметим, что 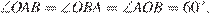 следовательно треугольник
следовательно треугольник  — равносторонний,
— равносторонний, 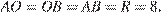
Ответ: 8.
Ответ: 8
11 Периметр равностороннего треугольника равен 30. Найдите его площадь делённую на 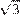 .
.
Решение.
Так как в равностороннем треугольнике все стороны равны, то сторона данного треугольника равна 10. Угол равностороннего треугольника равен 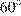 . Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
. Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
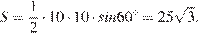
Ответ: 25.
----------
В открытом банке иррациональный ответ.
Ответ: 25
12. 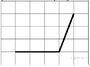 Найдите тангенс угла, изображённого на рисунке.
Найдите тангенс угла, изображённого на рисунке.
Решение.
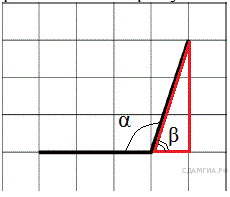
Углы  и
и 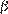 в сумме образуют развёрнутый угол
в сумме образуют развёрнутый угол  Значит,
Значит, 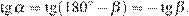
Рассмотрим прямоугольный треугольник, изображённый на рисунке. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
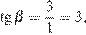
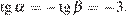
Ответ: −3.
Ответ: -3
13. Какие из следующих утверждений верны?
1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
2) Любые два равнобедренных треугольника подобны.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
| Модуль «Реальная математика» |
Решение.
Проверим каждое из утверждений.
1) «Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.»— верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
2) «Любые два равнобедренных треугольника подобны.» — неверно, так как углы, заключенные между пропорциональными сторонами, не равны.
3) «Любые два прямоугольных треугольника подобны.» — неверно, так как нет второго равного угла.
4) «Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.» — неверно, треугольник с такими сторонами является прямоугольным.
Ответ: 1.
Ответ: 1
14. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

*л. с. − лошадиная сила
Сколько рублей должен заплатить владелец автомобиля мощностью 185 л. с. в качестве налога за один год?
1)45
2)50
3)8000
4) 9250
Решение.
При мощности автомобиля в 185 л. с. он попадает в диапазон от 176—201 л. с., т. е. налоговая ставка составит 50 руб за л. с. в год.
Значит налог к уплате составит 185 · 50=9250.
Правильный ответ указна под номером 4.
Ответ: 4
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления во вторник в 6 часов утра. 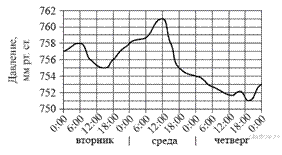
Решение.
Из графика видно, что значение давления во вторник в 6:00 равно 758 мм рт. ст.
Ответ: 758.
Ответ: 758
16. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма из этой прибыли должна пойти на выплату частным акционерам?
Решение.
Один процент от 40 млн равен: 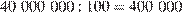 руб. На выплату частным акционерам пошло:
руб. На выплату частным акционерам пошло: 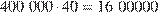 руб.
руб.
Ответ: 16000000.
Ответ: 16000000
17. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м? 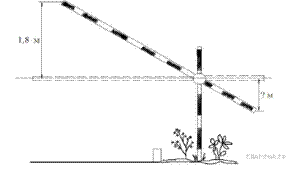
Решение.
Найдём синус угла, на который поднимается длинное плечо:
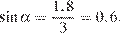
Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:

Таким образом, короткое плечо опустится на 0,6 м.
Ответ: 0,6.
Ответ: 0,6
18. На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сушёных белых грибах. Определите по диаграмме, в каком продукте содержание белков превышает 30%.
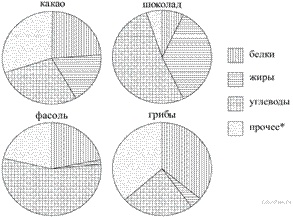
*К прочему относятся вода, витамины и минеральные вещества.
1) какао 2) шоколад 3) фасоль 4) грибы
Решение.
Из диаграмм видно, что содержание белков превышает 30% в грибах. Таким образом, верный ответ указан под номером 4.
Ответ: 4
19. В мешке содержатся жетоны с номерами от 2 до 51 включительно. Какова вероятность, того, что номер извлеченного наугад из мешка жетона является однозначным числом?
Решение.
Всего в мешке 50 жетонов. Среди них 8 с однозначными номерами. Таким образом, вероятность, того, что номер извлеченного наугад из мешка жетона является однозначным числом равна 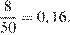
Ответ: 0,16
20 Чтобы перевести значение температуры по шкале Цельсия (t ° C) в шкалу Фаренгейта (t ° F), пользуются формулой F = 1,8 C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 158° по шкале Фаренгейта? Ответ округлите до десятых.
Часть 2
Решение.
Подставим в формулу значение переменной F:
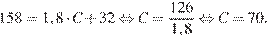
Ответ: 70.
Ответ: 70
21. Найдите значение выражения: 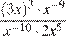 при
при 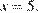
Решение.
Имеем:
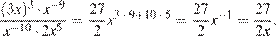
При  получаем:
получаем: 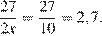
Ответ: 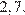
22. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию первая труба за одну минуту наполняет 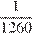 часть бассейна, а две трубы вместе за одну минуту наполняют
часть бассейна, а две трубы вместе за одну минуту наполняют 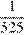 часть бассейна. Таким образом, одна вторая труба за минуту наполняет
часть бассейна. Таким образом, одна вторая труба за минуту наполняет 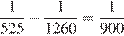 часть бассейна, то есть она наполняет весь бассейн за 15 часов.
часть бассейна, то есть она наполняет весь бассейн за 15 часов.
Ответ: 15.
23. Постройте график функции 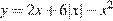 и определите, при каких значениях
и определите, при каких значениях  прямая
прямая 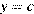 имеет с графиком ровно три общие точки.
имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
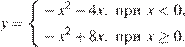
Этот график изображён на рисунке:
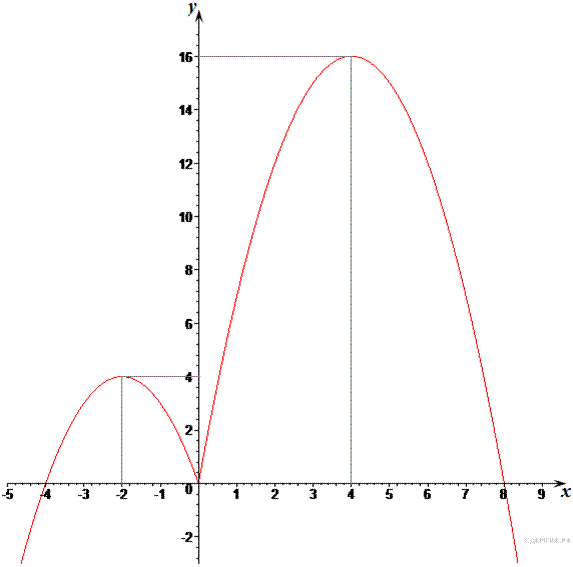
Из графика видно, что прямая 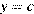 имеет с графиком функции ровно три общие точки при
имеет с графиком функции ровно три общие точки при 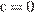 и
и 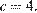
Ответ: 0; 4.
24. 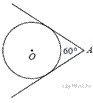 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Решение.
Опустим радиусы на каждую касательную. Соединим точки A и O. Получившиеся треугольники - прямоугольные, так как радиус, проведенный в точку касания, перпендикулярен касательной. По гипотенузе и катету эти треугольники равны, таким образом, мы получили, что угол, лежащий напротив катета равен 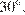 Катет, лежащий напротив угла в
Катет, лежащий напротив угла в 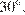 равен половине гипотенузы, тогда радиус равен 4.
равен половине гипотенузы, тогда радиус равен 4.
Ответ: 4.
25. 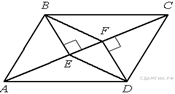 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Решение.
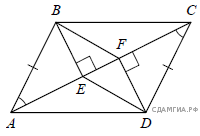
 — параллелограмм, поэтому стороны
— параллелограмм, поэтому стороны  и
и 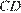 равны. Углы
равны. Углы  и
и 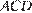 равны, как накрест лежащие при параллельных прямых
равны, как накрест лежащие при параллельных прямых  и
и 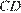 и секущей
и секущей  Рассмотрим треугольники
Рассмотрим треугольники 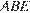 и
и 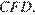 они прямоугольные, их гипотенузы равны и угол
они прямоугольные, их гипотенузы равны и угол  равен углу
равен углу  следовательно эти треугольники равны по гипотенузе и углу, значит, равны отрезки
следовательно эти треугольники равны по гипотенузе и углу, значит, равны отрезки 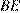 и
и 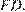
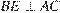 и
и 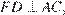 следовательно
следовательно 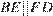 . Противоположные стороны четырёхугольника
. Противоположные стороны четырёхугольника  равны и параллельны, следовательно этот четырёхугольник — параллелограмм.
равны и параллельны, следовательно этот четырёхугольник — параллелограмм.
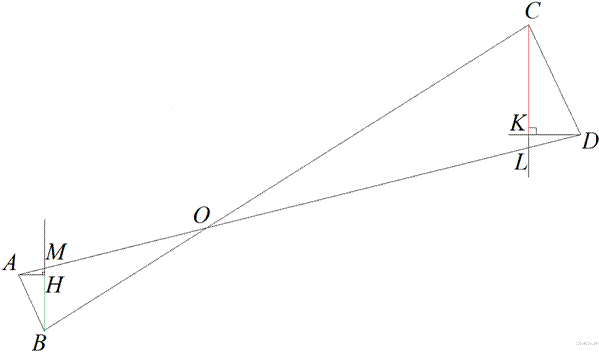
26. 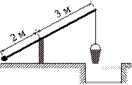 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Решение.
Введём обозначения, приведённые на рисунке. Здесь  — плечи "журавля" до опускания,
— плечи "журавля" до опускания,  — после,
— после,  — высота, на которую поднялся конец короткого плеча,
— высота, на которую поднялся конец короткого плеча,  — высота, на которую опустился конец длинного. Рассмотрим треугольники
— высота, на которую опустился конец длинного. Рассмотрим треугольники  и
и 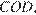 углы
углы  и
и 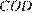 равны, как вертикальные, следовательно равны и углы при основаниях:
равны, как вертикальные, следовательно равны и углы при основаниях:
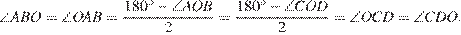
Следовательно, треугольники  и
и 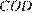 подобны по двум углам, то есть
подобны по двум углам, то есть 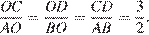
Рассмотри прямые  и
и  их пересекает секущая
их пересекает секущая  углы, обозначенные на рисунке 1 и 2 накрест лежащие и равны друг другу, следовательно прямые
углы, обозначенные на рисунке 1 и 2 накрест лежащие и равны друг другу, следовательно прямые  и
и 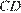 параллельны. Стороны углов 3 и 4 параллельны друг другу, следовательно они равны.
параллельны. Стороны углов 3 и 4 параллельны друг другу, следовательно они равны.
Рассмотрим треугольники 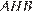 и
и  они прямоугольные, имеют равные углы, следовательно они подобны, значит:
они прямоугольные, имеют равные углы, следовательно они подобны, значит:

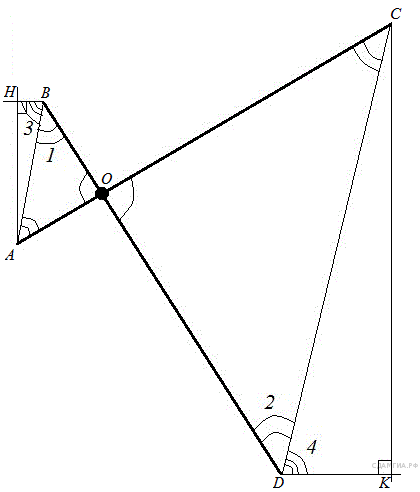
Ответ: 1,5.
Примечание
Можно привести несколько иное доказательство подобия треугольников 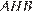 и
и  . На приведённой ниже картинке есть два маленьких треугольника обозначенные
. На приведённой ниже картинке есть два маленьких треугольника обозначенные 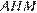 и
и 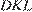 , они прямоугольные и одна пара углов равна друг другу как накрест лежащие при параллельных прямых, следовательно они подобны.
, они прямоугольные и одна пара углов равна друг другу как накрест лежащие при параллельных прямых, следовательно они подобны.
Затем, можно заметить, что у треугольников 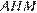 и
и  соответственные углы, не важно какие, равны друг другу, потому что их стороны параллельны, следовательно, треугольники подобны. Аналогично с треугольниками
соответственные углы, не важно какие, равны друг другу, потому что их стороны параллельны, следовательно, треугольники подобны. Аналогично с треугольниками  и
и  Из трёх пар подобий этих треугольников следует, что треугольники
Из трёх пар подобий этих треугольников следует, что треугольники  и
и  подобны.
подобны.
Вариант 3
Часть1
| Модуль «Алгебра» |
1. Расположите в порядке убывания числа 0,1327; 0,014; 0,13.
| 1) 0,1327; 0,014; 0,13 | 2) 0,014; 0,13; 0,1327 | 3) 0,1327; 0,13; 0,014 | 4) 0,13; 0,014; 0,1327 |
Решение.
Запишем все числа с четырьмя знаками после запятой и поразрядно сравним цифры в их записи:
0,1327,
0,0140,
0,1300.
Наибольшим является первое число, наименьшим — второе число.
Правильный ответ указан под номером 3.
Ответ: 3
2. На координатной прямой отмечены точки x и y.
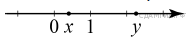
Какое из следующих неравенств верно?
1) 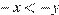 2)
2) 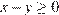
3) 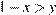 4)
4) 
Решение.
Заметим, что 0 < x < 1, 2 < y < 3. Тогда неравенство 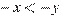 не верно. Для выражения x − y верно двойное неравенство −3 < x − y < −1. Для выражения 1 − x верно двойное неравенство 0 < 1 − x < 1. Для выражения
не верно. Для выражения x − y верно двойное неравенство −3 < x − y < −1. Для выражения 1 − x верно двойное неравенство 0 < 1 − x < 1. Для выражения 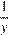 верно двойное неравенство
верно двойное неравенство 
Правильный ответ указан под номером 4.
Ответ: 4
3. Укажите наибольшее из чисел:
1) 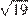 2)
2) 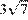 3)
3)  4)
4) 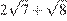
Решение.
Определим, между какими натуральными числами лежат числа, приведенные в ответах.
1) 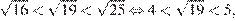
2) 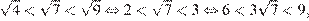
3) 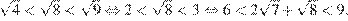
Таким образом, осталось сравнить второе и четвёртое число. Поскольку 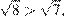 имеем
имеем 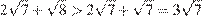 , т.е. четвёртое число больше второго.
, т.е. четвёртое число больше второго.
Правильный ответ указан под номером 4.
Ответ: 4
4. Найдите корни уравнения: 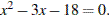 те их через точку с запятой в порядке возрастания.
те их через точку с запятой в порядке возрастания.
Решение.
По теореме, обратной теореме Виета, сумма корней равна 3, а их произведение равно −18. Тем самым, это числа −3 и 6.
Ответ: −3; 6.
Ответ: -3;6
5. На рисунке изображены графики функций вида 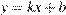 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов 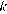 и
и 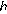 и графиками.
и графиками.
КОЭФФИЦИЕНТЫ
А) 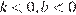
Б) 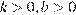
В) 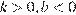
ГРАФИКИ
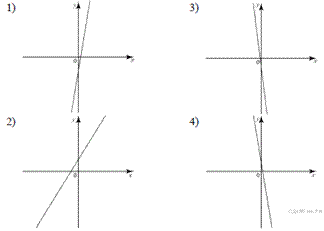
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В |
Решение.
Если значение функции возрастает с увеличением x, то коэффициент k положителен, если убывает — отрицателен. Значение b соответствует значению функции в точке x = 0, следовательно, если график пересекает ось ординат выше оси абсцисс, то значение b положит






