Постановка задачи.
Каждое экономическое, общественное и физическое явление находится во взаимодействии с другими явлениями. При изучении связей рассматриваемых явлений выделяют независимые признаки 
(факторные признаки) и результативные признаки 
. Факторные признаки влияют на результативные признаки.
Зависимости между признаками подразделяются на две категории – функциональные и корреляционные.
При функциональных связях каждому значению фактора соответствует вполне определенное значение результативного признака:
Примером функциональной связи служит закон Ома:
При корреляционной связи результативный признак зависит как от факторного признака , так и других факторов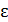 
:
В экономических явлениях широко присутствуют корреляционные связи.
Так, на прибыльность банка влияют процентные ставки (факторный признак) и другие признаки – объемы операций, заработная плата сотрудников, затраты на оборудование и т.д. Влияние прочих факторов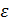 
на результат может быть незначительным, умеренным или существенным.
Методологию изучения статистической взаимосвязи рассмотрим на конкретном примере.
Пример
По семи областям проведено статистическое исследование по двум признакам: расходы на покупку продовольственных товаров в общих расходах и среднедневная заработная плата одного работающего. Каждый признак представлен выборкой из семи значений с целью уменьшения количества расчетов. Исследование выполнено случайным образом и его результаты отображены в таблице 1.1.
Таблица 1.1
| № п/п | Среднедневная заработная плата одного работающего, тыс. руб., X | Расходы на покупку продовольственных товаров в общих расходах, %, Y |
| 45,1 | 68,8 | |
| 59,0 | 61,2 | |
| 57,2 | 59,9 | |
| 61,8 | 56,7 | |
| 58,8 | 55,0 | |
| 47,2 | 54,3 | |
| 55,2 | 49,3 |
Требуется провести регрессионный и корреляционный анализ по двум выборкам для нахождения уравнения регрессии между двумя признаками. Уравнение регрессии позволит в дальнейшем формировать прогноз на будущее.
Решение
Выбор вида математической функции можно осуществить тремя методами: графическим, аналитическим и экспериментальным.
Построение графика зависимости результирующего признака от факторного.
Суть этапа заключается в построении зависимости результирующего признака от факторного на корреляционном поле (Рис.1). Порядок обозначения выборок через и обычно следует из условия задачи. Через семь точек на корреляционном поле можно попытаться провести аппроксимирующую функцию. Однако для маленьких выборок (меньше десяти) зачастую трудно установить вид зависимости признака от . Первый этап (построение графика) предполагает решение задачи на качественном уровне. Перейдем к количественному решению задачи.
Рисунок 1.1 – Корреляционное поле зависимости от
I – Линейная модель.
Цель этапа – установить уравнение связи двух переменных Y и X. Выберем простейшее линейное уравнение.
Регрессионный анализ.
Линейное уравнение имеет вид y = a + bx. Для расчета коэффициентов а и b составим систему нормальных уравнений, полученных по методу наименьших квадратов-МНК:
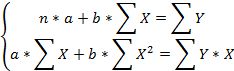
По исходным данным задачи рассчитаем: 
и их значения внесем в таблицу 1.2.
| Таблица 1.2 | ||||||||
| Линейная модель | ||||||||
| №п/п | 
| 
| 
| 
| 
| 
| 
| 
|
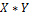
| 45,10 | 68,80 | 3102,88 | 2034,01 | 4733,44 | 61,10 | 7,71 | 11,20 | |
| 59,00 | 61,20 | 3610,80 | 3481,00 | 3745,44 | 56,23 | 4,97 | 8,12 | |
| 57,20 | 59,90 | 3426,28 | 3271,84 | 3588,01 | 56,86 | 3,04 | 5,08 | |
| 61,80 | 56,70 | 3504,06 | 3819,24 | 3214,89 | 55,25 | 1,45 | 2,56 | |
| 58,80 | 55,00 | 3234,00 | 3457,44 | 3025,00 | 56,30 | -1,30 | 2,36 | |
| 47,20 | 54,30 | 2562,96 | 2227,84 | 2948,49 | 60,36 | -6,06 | 11,16 | |
| 55,20 | 49,30 | 2721,36 | 3047,04 | 2430,49 | 57,56 | -8,26 | 16,75 | |
| Сумма | 384,30 | 405,20 | 22162,34 | 21338,41 | 23685,76 | 403,66 | 1,55 | 57,23 |
| Среднее значение | 54,90 | 57,89 | 3166,05 | 3048,34 | 3383,68 | - | - | 8,18 |
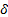
| 5,86 | 5,74 | - | - | - | - | - | - |
| 34,33 | 32,92 | - | - | - | - | - | - |
Коэффициенты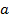 
и 
найдем из системы уравнений, например, путем подстановки, либо из дисперсионного анализа по формулам:
где,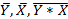 
- средние значения,
- среднее квадратическое отклонение
Уравнение линейной регрессии примет окончательный вид:
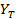– теоретические значения, в отличие от Y – фактических значений, заданных по условию задачи.
Теоретические значения 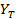будем получать из линейного уравнения путем подстановки фактических значений .
Экономический смысл коэффициента состоит в том, что с увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на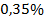 
.
Найдем среднюю ошибку аппроксимации 
.
Для нашей задачи выражено в процентах, поэтому:
Допустимый предел - не более 8-10%.
Таким образом, средняя ошибка аппроксимации почти вошла в допустимый предел.
Корреляционный анализ.
Цель этапа – рассчитать линейный коэффициент корреляции и установить силу связи между и .
Линейный коэффициент корреляции найдем по формуле
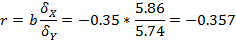
где, 
- среднее квадратическое отклонение по ,
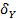- среднее квадратическое отклонение по ,
Значение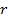 
, взятое по модулю, сравниваем со шкалой Чеддока (Приложение 1). Связь умеренная и обратная, поскольку r имеет отрицательное значение.
Определим коэффициент детерминации, который получим путем возведения коэффициента корреляции в квадрат.
Коэффициент детерминации
Коэффициент детерминации также указывает на влияние фактора на результат .
Вариация результата на 
объясняется вариацией фактора .
Оценка значимости уравнения регрессии.
Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера. Выдвигается гипотеза 
- фактор 
не оказывает влияния на результат . При этом коэффициент регрессии равен нулю,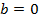 
.
Процесс оценки нулевой гипотезы сводится к сравнению фактического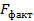 
и табличного 
значения критерия Фишера. Если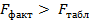 
, то нулевая гипотеза не отклоняется. Признается факт существования зависимости результата от 
так и для генеральных совокупностей Y и X.
Уравнение регрессии значимо.
Если 
, то нулевая гипотеза не отклоняется, но признается статистическая незначимость, ненадежность зависимости от . Уравнение регрессии незначимо, ненадежно. В этом случае требуется подбор другого уравнения регрессии.
Для линейной модели 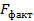равно:
где 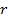– коэффициент корреляции,
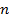– число показателей выборки.
вычисляют следующим образом:
1. Определяем К1, которое равно количеству факторов . В однофакторной модели 
, в двухфакторной 
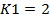. В нашей задаче модель однофакторная, поэтому 
.
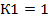2. Определяем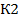 
, которое рассчитываем по формуле 
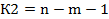, где 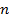– число значений выборки, 
– количество факторов. Для однофакторной модели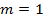 
. Для рассматриваемой задачи 
3. На пересечении столбца 
и 
находят 
по таблице Фишера с уровнем значимости 
(Приложение 2). Уровень значимости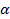 
- это вероятность отвергнуть гипотезу .
Вывод:
Следовательно, уравнение регрессии незначимо, ненадежно. Требуется подбор другого уравнения, например, одного из нелинейных.
II – Нелинейная модель
Предположим теперь, что результирующий фактор от факторного признака изменяется нелинейным образом. В качестве нелинейных моделей используют функции: степенную, показательную, экспоненциальную, гиперболическую. Для малых выборок, когда картина зависимости от просматривается плохо, требуется проверка всех моделей, а затем выбор наилучшей.
Выберем гиперболическую модель для уменьшения количества расчетов.
Уравнение равносторонней гиперболы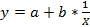 
Регрессионный анализ
Для определение параметров 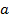и этого уравнения используется система нормальных уравнений по критерию метода наименьших квадратов:
Чтобы определить параметры уравнения гиперболы, необходимо привести ее к линейному виду. Для этого сделаем замену переменной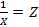 
и получим систему уравнений:
По исходным данным рассчитаем 
и внесем их в таблицу 1.3.
| таблица 1.3 | ||||||||||||||
| Нелинейная модель | ||||||||||||||
| №п/п | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||||
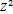
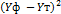
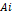
| 45,10 | 68,80 | 0,02 | 1,53 | 0,000492 | 4733,44 | 61,82 | 48,71 | 10,14 | 119,12 | |||||
| 59,00 | 61,20 | 0,02 | 1,04 | 0,000287 | 3745,44 | 56,31 | 23,90 | 7,99 | 10,98 | |||||
| 57,20 | 59,90 | 0,02 | 1,05 | 0,000306 | 3588,01 | 56,87 | 9,16 | 5,05 | 4,06 | |||||
| 61,80 | 56,70 | 0,02 | 0,92 | 0,000262 | 3214,89 | 55,50 | 1,44 | 2,11 | 1,41 | |||||
| 58,80 | 55,00 | 0,02 | 0,94 | 0,000289 | 3025,00 | 56,37 | 1,88 | 2,49 | 8,33 | |||||
| 47,20 | 54,30 | 0,02 | 1,15 | 0,000449 | 2948,49 | 60,78 | 41,99 | 11,93 | 12,86 | |||||
| 55,20 | 49,30 | 0,02 | 0,89 | 0,000328 | 2430,49 | 57,54 | 67,93 | 16,72 | 73,71 | |||||
| Сумма | 384,30 | 405,20 | 0,13 | 7,51 | 0,002413 | 23685,76 | 405,20 | 195,01 | 56,45 | 230,47 | ||||
| Сред знач | 54,90 | 57,89 | 0,02 | 1,07 | 0,000345 | 3383,68 | 27,86 | 8,06 | 32,92 | |||||
| δ | 5,86 | 5,74 | 0,002134 | |||||||||||
| δ^2 | 34,33 | 32,92 | 0,000005 | |||||||||||
Примечание. Значения Z рассчитываем до 4-го знака после запятой.
Коэффициенты 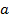и определим по формулам:
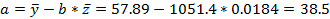
где,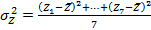 
Уравнение гиперболы примет вид:
Здесь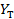 
- теоретическое значение, - фактическое (по условию задачи) значение.
Качество гиперболической модели определяет средняя ошибка аппроксимации:
Качество построения модели оценивается как хорошее, если 
не превышает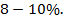 
Ошибка аппроксимации входят в допустимый предел.
Корреляционный анализ
Сила связи между результативным признаком и факторным для нелинейной модели определяется индексом корреляции, в то время как у линейной модели – коэффициентом корреляции.
Индекс корреляции:
Связь между признаками и умеренная.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака характеризует индекс детерминации 
Вариация результата на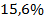 
объясняется вариацией фактора 
