Значительная часть задач производственной деятельности требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например число станков при загрузке оборудования, раскрой материалов, количество изготовленных единиц продукции, распределение транспортных средств по рейсам, продажа автомобилей, распределение самолетов по авиалиниям и др. Линейные задачи, решение которых должно быть получено в целых числах, называют задачами целочисленного программирования.
Задача целочисленного программирования формируется так же, как и задача линейного программирования, но включает дополнительное требование, состоящее в том, что значения переменных должны быть целыми неотрицательными числами, например,  станков,
станков,  самолетов,
самолетов,  человек.
человек.
Методы целочисленной оптимизации можно разделить на три основных группы: а) методы отсечения; б) комбинированные методы; в) приближенные методы. Рассмотрим один из методов отсечения – метод Гомори.
Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный оптимальный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
а) оно должно быть линейным;
б) должно отсекать найденный оптимальный нецелочисленный план;
в) не должно отсекать ни одного целочисленного плана.
Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением.
Алгоритм Гомори, основанный на симплексном методе, имеет простой способ построения правильного отсечения и содержит следующие этапы.
1. Задача линейного программирования решается без учета условия целочисленности симплексным или двойственным симплексным методом. Если все элементы оптимального плана – целые числа, то решение задачи заканчивается для задачи целочисленного программирования.
2. Если среди элементов оптимального решения есть нецелые числа, то необходимо выбрать элемент с наибольшей дробной частью и составить дополнительное ограничение (сечение), которое отсекает нецелочисленные решения.
Дополнительное ограничение выписывается в том случае, когда значение базисной переменной в оптимальном плане  дробное число. Тогда некоторые элементы
дробное число. Тогда некоторые элементы  в
в  ой строке симплексной таблицы также дробные числа. Обозначим через
ой строке симплексной таблицы также дробные числа. Обозначим через  и
и  целые части чисел
целые части чисел 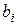 и
и  , т.е. наибольшие целые числа, не превышающие
, т.е. наибольшие целые числа, не превышающие 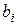 и
и  . Величины дробных частей
. Величины дробных частей  и
и  определяются как разности следующим образом:
определяются как разности следующим образом:  и являются положительными числами.
и являются положительными числами.
Тогда неравенство  , сформированное по
, сформированное по  ой строке симплексной таблицы, обладает всеми свойствами правильного отсечения.
ой строке симплексной таблицы, обладает всеми свойствами правильного отсечения.
3. Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу.
4. Полученная расширенная задача решается двойственным симплексным методом. Если новый оптимальный план будет целочисленным, то задача решена. В противном случае необходимо вернуться ко 2-му этапу алгоритма.
Если в процессе решения в симплексной таблице появится уравнение с нецелым свободным членом 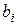 и целыми коэффициентами
и целыми коэффициентами  , то данная задача не имеет целочисленного оптимального решения.
, то данная задача не имеет целочисленного оптимального решения.
Пример. Маркетинговые исследования указали на необходимость освоения выпуска новой продукции. Поэтому на предприятии решено установить новое технологическое оборудование на освободившейся площади  . На приобретение оборудования двух видов выделено 6 млн. руб. Комплект первого вида оборудования стоимостью 1 млн. руб. устанавливается на площади
. На приобретение оборудования двух видов выделено 6 млн. руб. Комплект первого вида оборудования стоимостью 1 млн. руб. устанавливается на площади  и позволяет увеличить доход предприятия на 8 млн. руб. Комплект второго вида оборудования занимает площадь
и позволяет увеличить доход предприятия на 8 млн. руб. Комплект второго вида оборудования занимает площадь  и обеспечивает увеличение дохода предприятия на 5 млн. руб. Определить, какое количество технологического оборудования каждого вида следует закупить, чтобы обеспечить максимальное увеличение дохода предприятия от продажи продукции, выпускаемой новым оборудованием.
и обеспечивает увеличение дохода предприятия на 5 млн. руб. Определить, какое количество технологического оборудования каждого вида следует закупить, чтобы обеспечить максимальное увеличение дохода предприятия от продажи продукции, выпускаемой новым оборудованием.
Решение. Обозначим через  и
и 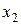 количество комплектов технологического оборудования соответственно первого и второго видов, через
количество комплектов технологического оборудования соответственно первого и второго видов, через  доход предприятия от продажи продукции, изготовленной новым оборудованием. Тогда математическая модель задачи имеет вид:
доход предприятия от продажи продукции, изготовленной новым оборудованием. Тогда математическая модель задачи имеет вид:
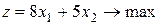 ,
,
при ограничениях:

Приведем задачу к каноническому виду, для чего введем дополнительные неотрицательные переменные 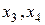 и решим ее симплексным методом.
и решим ее симплексным методом.

| Б | 
| 
| 
| 
| 
| 
| 
|

| ||||||||

| ||||||||
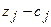
| -8 | -5 | -32 | -30 | ||||

| 
| 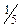
| ||||||

| 
| 
| 
| |||||
| 
| 
| 
| |||||

| 
| 
| 
| |||||

| 
| 
| 
| |||||
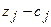
| 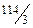
|
На третьей итерации получен оптимальный план задачи без учета условия целочисленности  , так как
, так как  .
.
По первому уравнению с переменной  , получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью
, получившей нецелочисленное значение в оптимальном плане с наибольшей дробной частью  , составляем дополнительное ограничение:
, составляем дополнительное ограничение:




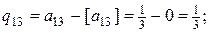
 .
.
Дополнительное ограничение имеет вид:
 .
.
Преобразуем полученное неравенство в уравнение:

коэффициенты которого введем дополнительной строкой в оптимальную симплексную таблицу, записанную выше.
Тогда получим:

| Б | 
| 
| 
| 
| 
| 
|

| 
| 
| 
| ||||

| 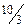
| 
| 
| ||||

| 
| 
| 
| ||||
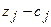
| 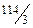
| ||||||

| -1 | ||||||

| -1 | ||||||

| -3 | ||||||
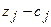
|
Применяя алгоритм двойственного симплексного метода (ключевой строкой является третья с отрицательным значением базисной переменной, а ключевым столбцом – столбец  с наименьшим по абсолютной величине значением частного от деления коэффициентов индексной строки на отрицательные коэффициенты ключевой строки), проводим одну итерацию, в результате которой получим оптимальное целочисленное решение:
с наименьшим по абсолютной величине значением частного от деления коэффициентов индексной строки на отрицательные коэффициенты ключевой строки), проводим одну итерацию, в результате которой получим оптимальное целочисленное решение:
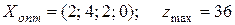 .
.
Таким образом, предприятию необходимо установить два комплекта оборудования первого вида и четыре комплекта второго вида. Это позволит максимально увеличить доход предприятия.
Следует заметить, что  площади останется неиспользованным, а деньги, выделенные на приобретение оборудования, будут полностью израсходованы.
площади останется неиспользованным, а деньги, выделенные на приобретение оборудования, будут полностью израсходованы.






