Методы решения задач линейного программирования
Графоаналитический метод
Свойства основной задачи линейного программирования связаны со свойствами выпуклых множеств.
Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую комбинацию.
Геометрический смысл этого определения состоит в том, что множеству вместе с его произвольными точками полностью принадлежит и прямолинейный отрезок, который их соединяет. Примерами выпуклых множеств являются прямолинейный отрезок, полуплоскость, круг, шар, куб, полупространство и др.
Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой линейной комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, круга – точки окружности, которая его ограничивает.
Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.
Если основная задача линейного программирования имеет оптимальный план, то целевая функция задачи принимает экстремальное значение в одной из вершин многогранника решений. Если экстремальное значение достигается более чем в одной вершине, то целевая функция принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.
Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник, каждая вершина которого определяет опорный план. Для одного из опорных планов (т.е. в одной из вершин многогранника решений) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов).
Вершину многогранника решений, в которой целевая функция принимает максимальное значение, можно найти достаточно просто, если задача в стандартной форме содержит не более двух переменных: 
при условиях  ,
,

Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость допустимых значений переменных соответственно с граничными прямыми
 .
.
Если система неравенств совместна, то областью допустимых решений задачи является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Решение задачи линейного программирования графоаналитическим методом включает следующие этапы.
1. На плоскости  строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Строят многоугольник решений.
4. Строят вектор-градиент целевой функции  , который указывает направление возрастания целевой функции. Координатами вектора
, который указывает направление возрастания целевой функции. Координатами вектора  являются коэффициенты целевой функции при переменных
являются коэффициенты целевой функции при переменных  и
и 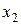 .
.
5. Строят линию уровня целевой функции, которая перпендикулярна вектору  и пересекает многоугольник решений, а затем передвигают ее в направлении вектора
и пересекает многоугольник решений, а затем передвигают ее в направлении вектора  до крайней угловой точки многоугольника решений, т.е. когда линия уровня примет положение опорной прямой. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции, если линия уровня целевой функции сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов.
до крайней угловой точки многоугольника решений, т.е. когда линия уровня примет положение опорной прямой. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции, если линия уровня целевой функции сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов.
6. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
7. Минимальное значение целевой функции находится путем передвижения линии уровня целевой функции в направлении, противоположном вектору  .
.
Пример 1.
Найдите экстремум линейной функции

при условиях-ограничениях:

Решение. Построим на плоскости  многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств.
многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств.
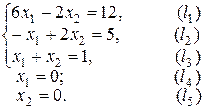
 Построив прямые
Построив прямые  , найдем соответствующие полуплоскости и их пересечение.
, найдем соответствующие полуплоскости и их пересечение.
Направление стрелок от каждой граничной прямой определяется путем непосредственной подстановки в соответствующее неравенство координат произвольно взятой, так называемой контрольной точки, например (0; 0), и при удовлетворении данного неравенства направляем стрелки в сторону контрольной точки, в противном случае – наоборот.
Многоугольником решений задачи является пятиугольник 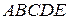 , координаты точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.
, координаты точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.
Для нахождения точек экстремума построим вектор  и линию уровня целевой функции
и линию уровня целевой функции  , которая перпендикулярна вектору
, которая перпендикулярна вектору  и пересекает пятиугольник
и пересекает пятиугольник 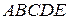 . Передвигая прямую
. Передвигая прямую  в направлении вектора
в направлении вектора  , найдем точку С, в которой линия уровня
, найдем точку С, в которой линия уровня  принимает положение опорной прямой. Следовательно, в точке С целевая функция имеет максимальное значение. Так как точка С получена в результате пересечения прямых
принимает положение опорной прямой. Следовательно, в точке С целевая функция имеет максимальное значение. Так как точка С получена в результате пересечения прямых  и
и  , то ее координаты удовлетворяют уравнениям этих прямых:
, то ее координаты удовлетворяют уравнениям этих прямых:

Решив систему уравнений, получим:  , откуда найдем максимальное значение целевой функции:
, откуда найдем максимальное значение целевой функции:
 .
.
По условию задачи линии уровня целевой функции параллельны прямой  , т.к. коэффициенты при переменных
, т.к. коэффициенты при переменных  и
и 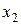 пропорциональны:
пропорциональны: 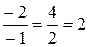 .
.
Следовательно, линия уровня  займет положение опорной прямой в точке В, С и в любой точке отрезка ВС, в которых целевая функция
займет положение опорной прямой в точке В, С и в любой точке отрезка ВС, в которых целевая функция 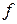 принимает одно и то же максимальное значение. Для определения координат точки В решим систему двух линейных уравнений:
принимает одно и то же максимальное значение. Для определения координат точки В решим систему двух линейных уравнений:

Максимальное значение целевой функции в точке В равно:
 .
.
Запишем множество оптимальных решений как выпуклую комбинацию угловых точек В и С:
 где
где  .
.
Подставив координаты угловых точек, получим:

Тогда  , где
, где  .
.
Подставляя любые значения  от 0 до 1, получим координаты множества точек отрезка ВС, в каждой из которых целевая функция принимает максимальное значение, равное 10.
от 0 до 1, получим координаты множества точек отрезка ВС, в каждой из которых целевая функция принимает максимальное значение, равное 10.
Для нахождения минимального значения целевой функции задачи перемещаем линию уровня  в направлении, противоположном вектору
в направлении, противоположном вектору  . Линия уровня
. Линия уровня  займет положение опорной прямой в вершине
займет положение опорной прямой в вершине  , где
, где  , а минимальное значение целевой функции равно:
, а минимальное значение целевой функции равно:
 .
.
Пример 2. В качестве второго примера на применение графоаналитического метода к решению задачи линейного программирования рассмотрим задачу, модель которой была приведена в качестве примера в разделе 1.1.
Построим на плоскости  многоугольник решений задачи. Для этого в неравенствах системы ограничений
многоугольник решений задачи. Для этого в неравенствах системы ограничений
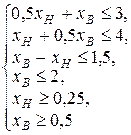
знаки неравенств заменим на знаки точных равенств:
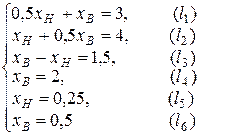
Построив полученные граничные прямые, найдем соответствующие полуплоскости допустимых значений переменных и их пересечение.

|
 .
.
Далее строим вектор-градиент  и линию уровня целевой функции
и линию уровня целевой функции  , которая перпендикулярна вектору
, которая перпендикулярна вектору  и пересекает шестиугольник
и пересекает шестиугольник  . Поскольку нас интересует максимальное значение целевой функции, то передвигая линию уровня
. Поскольку нас интересует максимальное значение целевой функции, то передвигая линию уровня  в направлении вектора
в направлении вектора  , найдем точку Е, в которой линия уровня
, найдем точку Е, в которой линия уровня  принимает положение опорной прямой. Следовательно, в точке Е целевая функция имеет максимальное значение. Так как точка Е получена в результате пересечения прямых
принимает положение опорной прямой. Следовательно, в точке Е целевая функция имеет максимальное значение. Так как точка Е получена в результате пересечения прямых 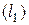 и
и  , то для определения ее координат решим систему уравнений:
, то для определения ее координат решим систему уравнений:
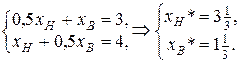
Максимальное значение целевой функции
 (тыс. руб.)
(тыс. руб.)
Таким образом, суточный объем производства краски для наружных работ должен быть равен  т, а для внутренних работ –
т, а для внутренних работ –  т. Доход от продажи в этом случае будет максимальным и составит
т. Доход от продажи в этом случае будет максимальным и составит  тыс. руб.
тыс. руб.
Симплексный метод решения задач линейного программирования
Для решения задач линейного программирования предложено немало различных алгоритмов. Наиболее эффективным среди них является алгоритм, известный под названием симплексный метод, или метод последовательного улучшения плана.
Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако, еще в 1939 г. идеи метода были разработаны российским математиком Л.В. Канторовичем.
Симплексный метод – это итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по угловым точкам области возможных решений до тех пор, пока не достигнет оптимального значения, в частности по угловым точкам многоугольника решений, полученного графоаналитическим методом.
В тех случаях, когда модель содержит т уравнений в основной системе ограничений, для построения пробных решений используется т переменных, принимающих некоторые положительные значения при нулевых значениях остальных переменных. Вначале предположим, что решение существует, причем оптимальное значение целевой функции конечно. В этом случае вычислительная процедура может быть представлена в следующей последовательности.
1. Выбираем т переменных, задающих допустимое пробное решение, и исключим эти переменные из целевой функции.
2. Проверим, нельзя ли за счет одной из переменных, приравненной вначале к нулю, улучшить значение целевой функции, придавая ей отличные от нуля (причем положительные) значения. Если это возможно, перейдем к третьему пункту, в противном случае прекратим вычисления.
3. Найдем предельное значение переменной, за счет которой можно улучшить значение целевой функции. Увеличение значения этой переменной допустимо до тех пор, пока одна из т переменных, вошедших в пробное решение, не обратится в нуль. Исключим из выражения для целевой функции только что упомянутую переменную и введем в пробное решение ту переменную, за счет которой результат может быть улучшен.
4. Разрешим систему т уравнений относительно переменной, вошедшей в новое пробное решение. Исключим эту переменную из выражения для целевой функции. Вернемся ко второму пункту.
Важно отметить, что предложенный алгоритм действительно приводит к оптимальному решению для любой модели линейного программирования за конечное число итераций, если система ограничений задачи совместна и оптимальное значение целевой функции конечно.
Симплексный метод основан на последовательном переходе от одного опорного плана задачи линейного программирования к другому, при этом значение целевой функции улучшается. Рассмотрим алгоритм симплексного метода на примере задачи рационального использования ресурсов.
Предприятие изготовляет п видов продукции, расходуя на это т видов сырья, запасы которых известны 
 ). Прибыль, получаемая от реализации единицы каждого вида продукции,
). Прибыль, получаемая от реализации единицы каждого вида продукции,  . Нормативы затрат сырья на изготовление единицы продукции составляют
. Нормативы затрат сырья на изготовление единицы продукции составляют  .
.
Необходимо составить такой план выпуска продукции, при котором прибыль от ее реализации будет максимальной.
Математическую модель задачи запишем следующим образом.
Определить план  , который удовлетворяет ограничениям
, который удовлетворяет ограничениям

и обеспечивает максимальное значение целевой функции 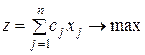 .
.
Алгоритм симплексного метода включает следующие этапы.
1. Составление начального опорного плана.
Система ограничений решаемой задачи задана в виде неравенств смысла  , правые части которых
, правые части которых 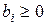 . Перейдем от системы неравенств к системе уравнений путем введения дополнительных неотрицательных переменных, каждая из которых определяет объем соответствующего неиспользованного ресурса. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:
. Перейдем от системы неравенств к системе уравнений путем введения дополнительных неотрицательных переменных, каждая из которых определяет объем соответствующего неиспользованного ресурса. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:
 ,
,
где  базисные переменные,
базисные переменные, 
 свободные переменные,
свободные переменные, 
Решим эту систему относительно базисных переменных:
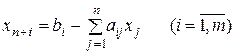 ,
,
а функцию цели перепишем в виде уравнения
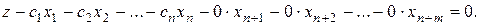
Дополнительные переменные вошли в выражение целевой функции с нулевыми коэффициентами, поскольку неиспользованные ресурсы прибыли не дают.
Полагая, что основные переменные 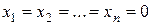 , получим начальный опорный план
, получим начальный опорный план  , и соответствующее этому плану значение целевой функции
, и соответствующее этому плану значение целевой функции  , что соответствует действительному положению дел, продукция не производится, ресурсы не используются, реализации и прибыли нет из-за отсутствия продукции.
, что соответствует действительному положению дел, продукция не производится, ресурсы не используются, реализации и прибыли нет из-за отсутствия продукции.
Реализация симплексного метода при решении задач линейного программирования осуществляется с помощью симплексных таблиц. В таблице выписаны соответствующие векторы  и
и  . Вектор
. Вектор  составлен из свободных членов системы основных ограничений. Среди соответствующих векторов есть т векторов, образующих базис. Их записывают в колонку «Б». Как видим, полагая свободные переменные равными нулю, из таблицы можно получить начальный опорный план задачи.
составлен из свободных членов системы основных ограничений. Среди соответствующих векторов есть т векторов, образующих базис. Их записывают в колонку «Б». Как видим, полагая свободные переменные равными нулю, из таблицы можно получить начальный опорный план задачи.
В таблице также записываются коэффициенты при переменных в целевой функции (первая строка), коэффициенты при базисных переменных в целевой функции (колонка  ). Строка
). Строка  называется индексной или строкой оценок. В ней расположены оценки векторов, которые рассчитываются так: находят сумму произведений компонент вектора на элементы колонки
называется индексной или строкой оценок. В ней расположены оценки векторов, которые рассчитываются так: находят сумму произведений компонент вектора на элементы колонки  и вычитают из полученного числа коэффициент при соответствующей переменной в целевой функции. Эти числа показывают, на сколько изменится значение целевой функции, если соответствующая переменная возрастет на единицу.
и вычитают из полученного числа коэффициент при соответствующей переменной в целевой функции. Эти числа показывают, на сколько изменится значение целевой функции, если соответствующая переменная возрастет на единицу.
Оценка вектора  число, стоящее на пересечении индексной строки и колонки
число, стоящее на пересечении индексной строки и колонки  , показывает значение целевой функции плана, записанного в данной таблице. Оно находится как сумма произведений элементов столбца
, показывает значение целевой функции плана, записанного в данной таблице. Оно находится как сумма произведений элементов столбца  на компоненты вектора
на компоненты вектора  .
.
Оценки векторов используются для проверки оптимальности плана.
2. Проверка плана на оптимальность.
Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум неотрицательны  , то план является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план неоптимальный и его можно улучшить. В этом случае переходим к следующему этапу алгоритма.
, то план является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план неоптимальный и его можно улучшить. В этом случае переходим к следующему этапу алгоритма.
3. Определение ключевого столбца и строки.
Из отрицательных коэффициентов индексной строки выбираем тот, который позволяет наибольшим образом изменить значение целевой функции. Он и определяет ключевой столбец, который показывает, какая переменная на следующей итерации перейдет из свободных в базисные и какой вектор войдет в базис.
Затем элементы столбца свободных членов симплексной таблицы делим на положительные элементы ключевого столбца. Результаты заносим в отдельный столбец 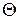 . Строка симплексной таблицы, соответствующая минимальному значению
. Строка симплексной таблицы, соответствующая минимальному значению  , является ключевой. Она определяет вектор, который на следующей итерации выйдет из базиса.
, является ключевой. Она определяет вектор, который на следующей итерации выйдет из базиса.
Элемент симплексной таблицы, находящийся на пересечении ключевого столбца и строки, называют ключевым и выделяют кружком.
4. Построение нового опорного плана.
Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана-Гаусса. Сначала заменим векторы в базисе, т.е. вместо 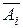 в базис войдет
в базис войдет  , соответствующий ключевому столбцу.
, соответствующий ключевому столбцу.
Разделим все элементы ключевой строки предыдущей симплексной таблицы на ключевой элемент и результаты деления запишем в строку следующей симплексной таблицы, соответствующую введенному в базис вектору  . В результате этого, на месте ключевого элемента в следующей симплексной таблице будем иметь 1, а в остальных клетках
. В результате этого, на месте ключевого элемента в следующей симплексной таблице будем иметь 1, а в остальных клетках  го столбца, включая клетку столбца индексной строки, записываем нули. Остальные новые элементы нового плана находятся по правилу прямоугольника:
го столбца, включая клетку столбца индексной строки, записываем нули. Остальные новые элементы нового плана находятся по правилу прямоугольника:
 ,
,
где  элемент старого плана,
элемент старого плана,  ключевой элемент,
ключевой элемент,  и
и  элементы старого плана, образующие прямоугольник с элементами
элементы старого плана, образующие прямоугольник с элементами 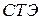 и
и  .
.
Затем возвращаемся ко второму этапу алгоритма – проверке нового плана на оптимальность.
Замечание 1. При решении задачи линейного программирования на минимум целевой функции признаком оптимальности плана являются неположительные значения всех коэффициентов индексной строки симплексной таблицы.
Замечание 2. Если в ключевом столбце все коэффициенты  , то функция цели неограничена на множестве допустимых планов, т.е.
, то функция цели неограничена на множестве допустимых планов, т.е.  и задача не имеет решения (в случае исследования
и задача не имеет решения (в случае исследования  на
на  ).
).
Замечание 3. Если в столбце  симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных переменных станут равными нулю). Вырожденные планы могут привести к зацикливанию, т.е. к многократному повторению процесса вычислений, не позволяющему получить оптимальный план. С целью исключения этого для выбора ключевой строки используют м етод Креко, который заключается в следующем. Элементы строк, имеющие одинаковые наименьшие
симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных переменных станут равными нулю). Вырожденные планы могут привести к зацикливанию, т.е. к многократному повторению процесса вычислений, не позволяющему получить оптимальный план. С целью исключения этого для выбора ключевой строки используют м етод Креко, который заключается в следующем. Элементы строк, имеющие одинаковые наименьшие  , делятся на предполагаемые ключевые элементы, а результаты заносятся в дополнительные строки. В качестве ключевой строки выбирается та, в которой раньше встретится наименьшее частное при чтении таблицы слева направо по столбцам. Например, таблица, содержащая три равных значения
, делятся на предполагаемые ключевые элементы, а результаты заносятся в дополнительные строки. В качестве ключевой строки выбирается та, в которой раньше встретится наименьшее частное при чтении таблицы слева направо по столбцам. Например, таблица, содержащая три равных значения  , имеет следующий вид:
, имеет следующий вид:
| Б | 
| 
| 
| 
| 
| 
| 
| 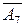
| 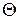
|

| 4: 2 = 2 | ||||||||

| 8: 4 = 2 | ||||||||

| -1 | 10: 5 = 2 |
Допустим, ключевым столбцом является 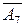 , который вводится в новый план. Тогда ключевым элементом может быть: 2, 4 или 5. Следуя указанному правилу, получаем таблицу:
, который вводится в новый план. Тогда ключевым элементом может быть: 2, 4 или 5. Следуя указанному правилу, получаем таблицу:

| 
| 
| 
| 
| 
| 
| 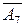
|
| 1,5 | 0,5 | ||||||
| 0,25 | 0,25 | ||||||
| 2,4 | -0,2 | 0,2 | 0,2 |
Сравниваем последовательно слева направо полученные частные по столбцам. В первом и втором столбце все частные одинаковы, а в третьем столбце наименьшее частное 1,5 в первой строке, следовательно, эта строка и будет ключевой с ключевым элементом 2.
Замечание 4. Если в оптимальный план вошла дополнительная переменная 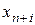 , то при реализации такого плана имеются неиспользованные ресурсы
, то при реализации такого плана имеются неиспользованные ресурсы  го вида, полученном в столбце свободных членов симплексной таблицы.
го вида, полученном в столбце свободных членов симплексной таблицы.
Замечание 5. Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий вектору, не вошедшему в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет бесчисленное множество оптимальных планов. Вектор, соответствующий указанному столбцу, можно ввести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных.
Пример.
Предприятие выпускает три вида продукции: А, В, С, используя при этом три вида ресурсов:  . Известны удельные расходы ресурсов, их запасы и прибыль, получаемая от реализации единицы продукции. Указанные данные размещены в таблице.
. Известны удельные расходы ресурсов, их запасы и прибыль, получаемая от реализации единицы продукции. Указанные данные размещены в таблице.
Необходимо определить какое количество продукции соответствующего вида должно изготовить предприятие из имеющихся ресурсов, чтобы, реализовав изготовленную продукцию, получить максимальную прибыль.
| Ресурсы | А | В | С | Запас |
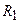
| ||||

| ||||

| ||||
| Прибыль |
Решение. Запишем математическую модель задачи.
Определим план  , который удовлетворяет условиям
, который удовлетворяет условиям

и обеспечивает максимальное значение целевой функции
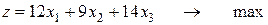 .
.
Для построения начального опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных неотрицательных переменных 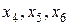 :
:

Очевидно, что переменные 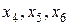 в этой системе являются базисными, а
в этой системе являются базисными, а  свободными.
свободными.
Следует отметить, что смысл переменных  и
и  неиспользованные ресурсы вида
неиспользованные ресурсы вида 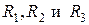 соответственно и поэтому эти переменные войдут в выражение целевой функции с нулевыми коэффициентами:
соответственно и поэтому эти переменные войдут в выражение целевой функции с нулевыми коэффициентами:
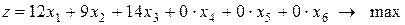
Полагая, что свободные переменные  , получим начальный опорный план
, получим начальный опорный план 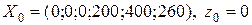 , в котором базисные переменные
, в котором базисные переменные  . Следовательно, продукция не изготовляется и не реализуется, ресурсы не используются, а прибыль равна нулю. Полученный начальный опорный план запишем в симплексную таблицу.
. Следовательно, продукция не изготовляется и не реализуется, ресурсы не используются, а прибыль равна нулю. Полученный начальный опорный план запишем в симплексную таблицу.

| Б | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|

| |||||||||||
| 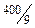
| 
| |||||||||
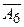
| 
| 
| |||||||||
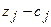
| -12 | -9 | -14 | 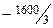
| -240 | -560 |
Начальный опорный план неоптимальный, так как в индексной строке находятся отрицательные коэффициенты: 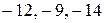 .
.
Учитывая экономический смысл элементов индексной строки, за ключевой столбец выбираем столбец  , а затем по наименьшему элементу столбца
, а затем по наименьшему элементу столбца  за ключевую строку – первую строку.
за ключевую строку – первую строку.
Ключевой элемент равен 5 и находится на пересечении ключевого столбца и ключевой строки и выделен в таблице.
Формируем следующую симплексную таблицу. Вместо вектора  в базис войдет вектор
в базис войдет вектор  . Первая строка в этой таблице получена в результате деления всех элементов первой строки первой симплексной таблицы на ключевой элемент
. Первая строка в этой таблице получена в результате деления всех элементов первой строки первой симплексной таблицы на ключевой элемент  . На месте ключевого элемента во второй таблице получаем 1. В остальных клетках столбца
. На месте ключевого элемента во второй таблице получаем 1. В остальных клетках столбца  второй таблицы записываем нули. Столбцы
второй таблицы записываем нули. Столбцы 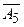 и
и 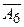 переносятся во вторую симплексную таблицу без изменения, т.к. они остались в базисе.
переносятся во вторую симплексную таблицу без изменения, т.к. они остались в базисе.
Таким образом, во второй симплексной таблице заполнены первая строка и столбцы  ,
, 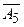 и
и 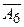 . Все остальные элементы второй симплексной таблицы, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из первой таблицы четыре числа, которые расположены в вершинах прямоугольника и всегда включают ключевой элемент
. Все остальные элементы второй симплексной таблицы, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из первой таблицы четыре числа, которые расположены в вершинах прямоугольника и всегда включают ключевой элемент  . Во второй вершине по диагонали находится старое значение элемента, например, значение целевой функции
. Во второй вершине по диагонали находится старое значение элемента, например, значение целевой функции  , которое указывает на место расположения нового элемента
, которое указывает на место расположения нового элемента  во второй симплексной таблице. Третий элемент
во второй симплексной таблице. Третий элемент  и четвертый элемент
и четвертый элемент  завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента во второй симплексной таблице находится из выражения:
завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента во второй симплексной таблице находится из выражения:
 .
.
Элементы второй строки определяются аналогично:

Аналогично проводятся расчеты по всем строкам таблицы, включая индексную.

| Б | 
| 
| 
| 
| 
| 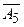
| 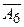
| 
|

| 
| 
| 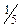
| ||||||
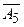
| -1 | ||||||||
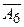
| 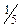
| 
| 
| ||||||
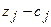
| 
| 
| 
| -32 |
Контроль. Из второй симплексной таблицы можно выписать план рассматриваемой задачи  и значение целевой функции на нем
и значение целевой функции на нем  .
.
Полученный план неоптимальный, поскольку в индексной строке находится отрицательный коэффициент:  .
.
На третьей итерации (третья симплексная таблица) получаем план, который является оптимальным, т.к. все коэффициенты в индексной строке 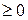 .
.

| Б | 
| 
| 
| 
| 
| 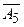
| 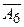
|

| 
| 
| 
| |||||

| 
| 
| 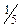
| |||||
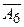
| 
| 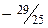
| 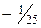
| |||||
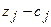
| 
| 
| 
|
Оптимальный план можно записать так:  .
.
Следовательно, предприятие для получения максимальной прибыли в размере 592 денежных единицы должно из имеющихся ресурсов изготовить и реализовать 40 единиц продукции вида А и 8 единиц продукции вида С, а продукцию вида В совсем не производить. При этом ресурсы  и
и  будут использованы полностью, а ресурс
будут использованы полностью, а ресурс  останется в количестве 12 единиц.
останется в количестве 12 единиц.
В индексной строке последней симплексной таблицы небазисные столбцы имеют ненулевые оценки, поэтому полученный оптимальный план является единственным.






