Большинство технических измерений осуществляют однократно. Это, в первую очередь, обусловлено экономическими соображениями. Кроме того, есть измерения, которые вообще нельзя осуществить многократно. Это относится к объектам, которые в процессе измерения разрушаются.
При однократных измерениях для оценки результата используются одно–единственное значение отсчета показаний прибора. Очевидно, что это измерение может содержать инструментальную, методическую и субъективную (личную) составляющие, каждая из которых, в свою очередь, состоит из систематической и случайной частей.
Выявление и оценка всех этих составляющих является главной проблемой при однократном измерении. Трудность такого оценивания заключается в полном отсутствии информации о законах распределения.
Инструментальная систематическая погрешность может быть выявлена поверкой СИ, а методическая – тщательным анализом используемого метода.
По нормируемым метрологическим характеристикам СИ можно определить только предельные значения 
iпр погрешности измерения , т. е. такие, для которых с 
=1 можно считать, что действительные значения 
iпр.
Если все составляющие iпр двузначным и симметричны, т. е. iпр =± А, то модуль суммарной погрешности пр будет равен
, (2.29)
тогда результат может быть представлен в виде
при 
=1. (2.30)
Составляющие случайных погрешностей могут быть заданы своими СКО 
, найденными предварительно опытным путем по результатам многократных наблюдений. В этом случае суммарное СКО вычисляется по формуле (2.15), а доверительный интервал по формуле (2.17).
Если случайные составляющие погрешности заданы доверительными интервалами с равными доверительными вероятностями , то выражение для суммарного интервала будет иметь вид (2.18).
Для исключения брака (грубой погрешности) при однократном измерении рекомендуется повторить его 2-3 раза, приняв за результат среднее арифметическое. Более подробно однократные измерения рассмотренные МИ1552–86 «ГСИ. Измерения прямые однократные».
Пример. Оценить результат однократного измерения падения напряжения 
В на сопротивлении R =2 Ом, которое измерено вольтметром с пределом измерения 1,5 В, внутренним сопротивлением RV =1 кОм, и пределом допускаемой погрешности 0,5% от верхнего предела. Условие измерения: температура 20°С, магнитное поле 400 А/м. Дополнительные погрешности показаний вольтметра от влияния магнитного поля подсчитано по паспортным данным и находится в пределах ±0,75%, дополнительная погрешность от температуры отсутствуют, так как измерение произведено при нормальных условиях (20°С).
Рис. 2.8. Иллюстрация к примеру
Инструментальная составляющая погрешность измерения состоит из основной и дополнительной погрешности. При показании вольтметра 0,8 В предел допускаемой относительной погрешности вольтметра на этой отметке равен
Методическая погрешность обусловлена конечным значением входного сопротивления вольтметра RV и будет равна (2.1)
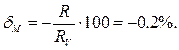
Ее, как систематическую погрешность, необходимо исключить из результата в виде поправки
Тогда за результат измерения принимаем исправленное значение
.
Найдем границы относительной погрешности результата суммированием составляющих
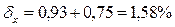
и для абсолютной погрешности
Округляя, результат измерения заменим в виде
при =1.
Косвенные измерения
Часто возникает необходимость определить результирующую погрешность от нескольких, функционально связанных погрешностей. В этом случае искомое значение величины находят на основе измерения других величин в соответствии с зависимостью
(2.31)
Пусть 
распределены по нормальному закону, измерения равноточные, а погрешности составляющих не коррелированны.
Если независимые переменные 
измерены с абсолютными погрешностями 
, то (2.31) примет вид:
Разложим правую часть в ряд Тейлора, оставив члены разложения, содержащие в первой степени
Отсюда абсолютная погрешность 
будет равна
(2.32)
а относительная
(2.33)
Если заданы СКО результатов измерений, то результирующее значение СКО будет
(2.34)
а доверительные границы случайной погрешности
где 
–коэффициент Стьюдента для 
степени значимости.
Методика обработки результатов косвенных измерений приведена в МИ2083-90 «ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей».
Пример. Измеряется скорость в соответствии с выражением 
. Необходимо определить абсолютную погрешность.
Разлагая в ряд Тейлора получим
тогда выражение для абсолютной погрешности в соответствии с (2.32)
