Результаты многократных наблюдений, получаемых при прямых измерениях величины X, называются равноточными, если они независимые, одинаково распределенные случайные величины, а измерения осуществляются одним наблюдением в одинаковых условиях с помощью одного и того же средства измерений.
Статистическая обработка экспериментального материала выполняется в соответствии с ГОСТ 8.207-76.
Рассмотрим группу 
результатов наблюдений.
Оценкой рассеяния результатов наблюдений в группе относительно среднего 
(2.6) будет 
(2.7). Так как число наблюдений в группе ограничено, то повторив заново серию наблюдений такого же объема n, мы получим другое значение . Повторяя серии n наблюдений и вычисляя каждый раз среднее значение, мы убедимся, что имеет своё рассеяние, числовой характеристикой которого является СКО среднего арифметического .
При обработке многократных наблюдений необходимо учитывать следующие факторы:
· обрабатывается группа наблюдений ограниченного объёма n;
· эта группа может содержать грубые погрешности (промахи);
· результаты наблюдений могут содержать систематическую погрешность;
· распределение случайных погрешностей может отличаться от нормального.
Согласно ГОСТ 8.207-76 обработка результатов наблюдений производится в последовательности:
1. Исключаются известные систематические погрешности из результатов наблюдений.
2. Определяют границы неисключенной систематической погрешности (остатка) результата измерений.
3. Вычисляется среднее арифметическое исправленных результатов наблюдений, которое принимается за результат измерения .
4. Вычисляется оценка СКО результатов наблюдений 
.
5. Проверяется наличие в группе наблюдений грубых погрешностей. Если они есть, то их исключают из группы и вновь повторяют вычисление и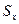 
.
6. Вычисляют оценку СКО среднего арифметического .
7. Проверяют гипотезу о принадлежности результатов наблюдений к нормальному закону распределения.
8. Вычисляют доверительные границы случайной погрешности (случайной составляющей погрешности).
9. Вычисляют доверительные границы погрешностей результата измерения.
Основной нормативный документ для выполнения многократных измерений является ГОСТ 8.207-76, а также – ГОСТ 11.002-73 (Прикладная статистика. Правила оценки нормальности результатов наблюдений), ГОСТ 11.004-74 (Прикладная статистика. Правила определения оценок и доверительных границ для параметров нормального распределения).
Среднее арифметическое исправленных результатов наблюдений (измерений), принимаемое за результат измерения, вычисляют по формуле
(2.20)
где n - число равноточных наблюдений; 
- i -й результат наблюдений.
Оценку СКО результата наблюдения 
вычисляют по приближенной формуле Бесселя
(2.21)
Эта оценка характеризует степень рассеяния результатов наблюдений относительно среднего арифметического и определяется условиями измерения (метрологическими характеристиками средства измерения, психофизическими качествами экспериментатора и др.).
В результате измерительного эксперимента получаем выборку 
, среди значений которой могут быть значения, существенно отличающихся от других. Принятие решения об исключении (или сохранении) таких значений осуществляют методами статистических гипотез. Для проверки гипотезы о том, что результаты не содержат грубой погрешности (брака), вычисляют величину.
(2.22)
где 
–экстремальные результаты наблюдений.
Полученные результаты 
сравнивают с наибольшим значением 
, которое случайная величина 
может принять по чисто случайным причинам.
Значение табулированы (см. Приложение 1) для заданной доверительной вероятности 
или уровне значимости 
. Если 
не принадлежит нормальной совокупности, то окажется справедливой зависимость
(2.23)
Доверительные границы случайной составляющей погрешности в соответствии со стандартом устанавливают для совокупности 
, принадлежащей нормальному распределению. Проверку нормальности, согласно ГОСТ 11.006–74, при n > 50, проводят по критериям Пирсона или Мизеса–Смирнова.
При 15 < n < 50 используют двойной составной q– критерий.
Критерий 1. Вычисляют отношение
(2.24)
где 
– смещенная оценка СКО, вычисляемая по формуле
Результаты наблюдений можно считать нормально распределенными, если
(2.25)
где 
и 
–квантили распределения статистики d (см. Приложение 2); q 1– заранее выбранный уровень значимости.
Это условие является необходимым, но не достаточным. Поэтому используют второй критерий.
Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей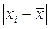 
превысили значение 
, 
– верхняя квантиль распределения нормированной функции Лапласа, для вероятности Р /2 (см. Приложение 3).
Значение вероятности Р можно определить по выбранному уровню значимости 
и по числу результатов наблюдений n из соответствующих таблиц.
В случае, если при проверке нормальности распределения результатов наблюдений хотя бы один из критериев не выполняется, то считают, что данная совокупность не принадлежит нормальному распределению.
При n < 15 принадлежность к нормальному закону не проверяется, а доверительные границы случайной погрешности результата измерений определяют лишь в том случае, если есть сведения о нормальности распределения хi.
Доверительные границы 
случайной погрешности результата измерения при заданной доверительности вероятности 
вычисляют по формуле
где 
- коэффициент Стьюдента, который определяют из таблиц по числу степеней свободы (n –1) и доверительной вероятности 
(см. Приложение 4).
В ГОСТ 8.207-76 даны рекомендации по определению доверительных границ неисключенной систематической погрешности результата измерений. Она образуется из неисключенных систематических составляющих погрешностей метода, средств измерений, погрешностей поправок и др.
Закон распределения 
(если нет других сведений) принимают равномерным. В этом случае границы неисключенной систематической погрешности результата измерения вычисляют по формуле
(2.24)
где 
– граница i –й неисключенной составляющей погрешности; k – коэффициент, зависящей от доверительной вероятности (
); m –число неисключенных составляющих, если m < 4, то коэффициент k выбирают по графику зависимости 
[2.5 стр.75].
Доверительную вероятность 
принимают такой же, что при вычислении границ 
.
Границы погрешности результата измерений определяют в зависимости от соотношения величин не исключенной систематической составляющей и СКО среднего арифметического.
Если 
, то не исключенной систематической погрешностью можно пренебречь и принять границы погрешности результата 
. Если 
, то случайной погрешностью можно пренебречь и принять границы погрешности результата 
.
Если не выполняются оба неравенства, то вычисляют СКО результата измерения
, (2.25)
а границы погрешности в этом случае будут равны
, (2.26)
где
Согласно ГОСТ при симметричном доверительном интервале погрешности результат измерения представляют в форме
, при 
. (2.27)
Если данные о видах функции распределения отсутствуют, то результат измерения записывают в виде
(2.28)
Оценки 
могут выражаться в данных измеряемой величины. Допускается выражать их в относительной или приведенной формах.
